Lines and Angles Các chủ đề lớp 7
Các chủ đề và chủ đề phụ về đường thẳng và góc lớp 7 là:
- Giới thiệu
- Góc liên quan
- Các góc bổ sung
- Góc độ bổ sung
- Góc liền kề
- Cặp tuyến tính
- Các góc đối diện theo phương thẳng đứng
- Các cặp dòng
- Đường giao nhau
- Chuyển ngang
- Các góc được tạo bởi mặt cắt ngang
- Chuyển ngang của các đường song song
- Kiểm tra các đường song song
Lines and Angles Class 7 Notes
Chúng ta hãy thảo luận về các khái niệm được đề cập trong lớp 7 đường thẳng và góc.
Giới thiệu về Đường và Góc
Để đề cập đến giáo trình Lines and Angles lớp 7, chúng tôi đã khái quát các chủ đề ở đây. Đọc lần lượt các chủ đề dưới đây để hiểu các khái niệm về đường thẳng và góc.
Hàng:
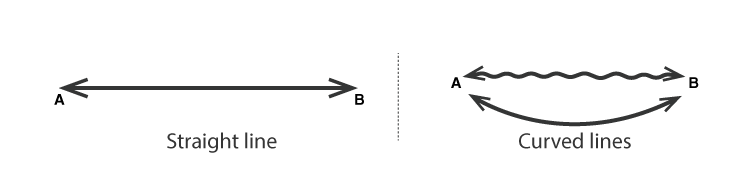
Đường thẳng là một hình thẳng không có điểm cuối và kéo dài vô hạn theo các hướng ngược nhau.

Cá đuối:
Tia là một đường thẳng, bắt đầu từ một điểm cố định và chuyển động theo một hướng.


Phân đoạn dòng
Một phần của đoạn thẳng được tạo thành với hai điểm xác định được gọi là Đoạn thẳng. Một đường là một hình một chiều và không có độ dày.


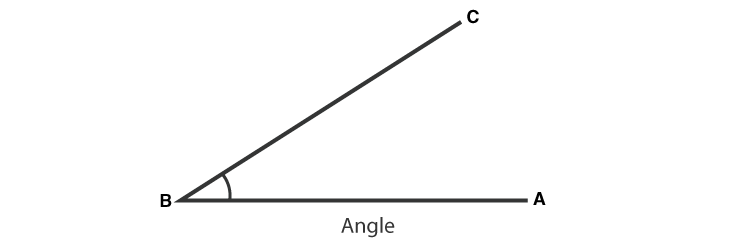
Góc
Khi chúng ta nối hai đoạn thẳng tại một điểm, một góc được hình thành, hay chúng ta có thể nói, Góc là sự kết hợp của hai đoạn thẳng tại một điểm cuối chung. Điểm chung này được gọi là Đỉnh của góc và hai đoạn thẳng là cạnh hoặc nhánh của góc được tạo thành.

Các loại góc
Về cơ bản có 6 loại góc là:
- Góc phía sau: Nếu một góc nhỏ hơn 90 độ, thì nó được gọi là góc phía sau
- Góc Obtuse: Nếu một góc lớn hơn 90 độ, thì nó được gọi là Obtuse Angle
- Góc phải: Nếu một góc chính xác là 90 độ, thì nó được gọi là Góc phải.
- Góc thẳng: Nếu một góc chính xác là 180 độ, thì nó được gọi là Góc thẳng.
- Góc phản xạ: Nếu góc lớn hơn 180 độ nhưng nhỏ hơn 270 độ, nó được ký hiệu là góc phản xạ.
- Góc đầy đủ: Góc 360 độ được gọi là góc đầy đủ.


Góc liên quan
Ngoài điều này ra, các góc độ khác nhau là:
Góc bổ sung: Tổng số đo của hai góc là 90 °
Góc bổ sung: Tổng số đo của hai góc là 180 °
Góc kề: Các góc kề nhau có một đỉnh chung và một nhánh chung nhưng không có điểm bên trong chung
Cặp pháp tuyến: Cặp góc thẳng là cặp góc kề nhau mà các cạnh không chung nhau là các tia đối nhau.
Góc đối diện theo phương thẳng đứng: khi hai đường thẳng cắt nhau, các góc đối diện theo phương thẳng đứng sẽ bằng nhau.
Các cặp dòng
Các đường giao nhau: Hai đường thẳng cắt nhau nếu chúng có điểm chung. Điểm chung O là giao điểm của chúng.
Ngang: Một đường cắt hai hoặc nhiều đường tại các điểm phân biệt được gọi là đường ngang.
Các góc tạo bởi đường cắt ngang: Có các góc khác nhau được tạo thành khi đường cắt ngang cắt các đường thẳng. Họ đang:
- Góc nội thất
- Các góc ngoại thất
- Các cặp góc nội thất thay thế
- Các cặp góc bên ngoài thay thế
- Các cặp góc tương ứng
- Các cặp góc nội thất trên cùng một phía của đường ngang
Transversal of Parallel Lines: Chúng ta biết rằng các đường thẳng song song là những đường thẳng không gặp nhau ở đâu. Sự chuyển tiếp của các đường thẳng song song tạo ra kết quả khá thú vị.
Kiểm tra các đường song song
Nếu một đường ngang cắt hai đường thẳng sao cho mỗi cặp góc tương ứng có số đo bằng nhau.
Tương tự, nếu một đường ngang cắt hai đường thẳng thì mỗi cặp góc trong thay thế bằng nhau.
Ngoài ra, nếu mặt cắt ngang cắt các đường thẳng, thì mỗi cặp góc bên trong ở cùng một phía của mặt cắt ngang là bổ sung.
Trong những trường hợp này, các dòng phải ở trong điều kiện song song.\
Xem thêm: