Làm thế nào để tìm Foci của một hình elip?
Giả sử rằng “S” là tiêu điểm và “l” là ma trận trực tiếp của một hình elip. Gọi Z là chân của đường trung trực y ‘từ S trên ma trận trực tiếp l. Gọi A và A ‘là các điểm chia SZ theo tỉ lệ e: 1. Gọi C là trung điểm của AA ‘là gốc tọa độ.
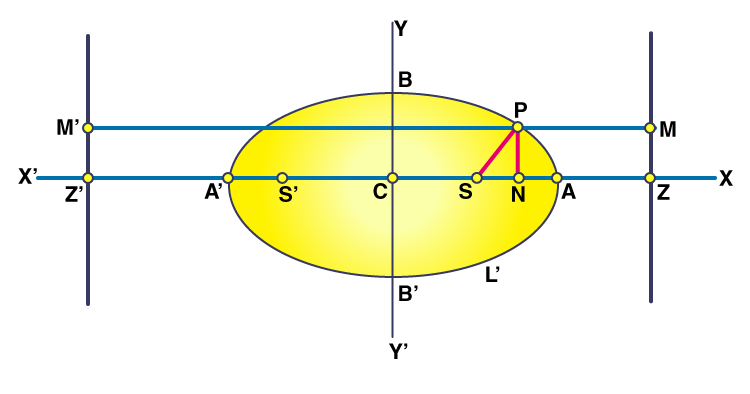

Cho CA = a
⇒ A = (a, 0) và A ‘= (- a, 0).
Bây giờ (AS) / (AZ) = (e) / (1) = (A’S) / (A’Z)
⇒ SA = eAZ & SA ‘= eA’Z
⇒ CA-CS = e (CZ-CA) ———> 1
⇒ SC + CA ‘= e (A’C + CZ) ———> 2
Thêm 1 và 2, chúng tôi nhận được
CA + CA ‘= e (2CZ)
⇒ 2a = 2e * CZ
⇒ CZ = (a) / (e)
⇒ Phương trình của ma trận trực tiếp là x = (a) / (e)
Trừ đi 1 và 2, ta được
2CS = e (2CA) = e * 2a
⇒ CS = a
⇒ Tiêu điểm, S = (ae, 0)
Do đó, Foci = (ae, 0) & (-ae, 0) do tính đối xứng.
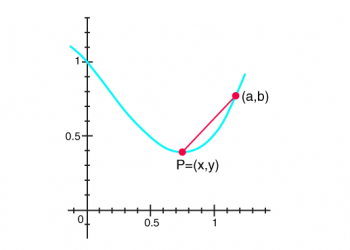
Ta coi P (x, y) là điểm trên elip và PM là khoảng cách vuông góc từ P đến l
Theo định nghĩa của Ellipse,
(SP) / (PM) = e
⇒SP = và PM
⇒SP 2 = e 2 PM 2
(x-ae) 2 + y 2 = e 2 [(x 2 + a 2 ) / (e 2 ) – (2ax) / (e)]
x 2 / a 2 + (y 2 ) / (a 2 (1-e 2 )) = 1
e <1, 1-e 2 > 0
⇒ a 2 (1-e 2 )> 0
Hãy để nó là b 2
Sau đó,
(x 2 / a 2 ) + (y 2 / b 2 ) = 1
Đó là phương trình của một elip.
Thuộc tính Focus-Directrix của một hình elip
Xét hình elip (x 2 / a 2 ) + (y 2 / b 2 ) = 1.
Vẽ các đường thẳng ZD và ZD ‘có phương trình lần lượt là x = a / e và x = -a / e
Gọi P (x, y) là hai điểm bất kỳ trên elip. Gọi D ‘PD song song với trục x.

Các foci là F (c, o) và F ‘(-c, o).
Bây giờ PF + PF ‘= 2a (theo định nghĩa của một hình elip)
√ [(xc) 2 + y 2 ] + √ [(x + c) 2 + y 2 ] = 2a
√ [(x + c) 2 + y 2 ] = 2a – √ [(xc) 2 + y 2 ]
(x + c) 2 + y 2 = 4a 2 + (xc) 2 + y 2 -4a√ [(xc) 2 + y 2 ]
√ [(xc) 2 + y 2 ] = [a- (c / a) x]
PF = a- (c / a) x
PF = e [(a / e) – (c / de) x] trong đó c = ae
PF = e [(a / e) -x]
PF = e. PD ——– (1)
Hơn nữa PF + PF ‘= 2a
PF ‘= 2a – PF
2a-a + ex = a + ex = e [(a / e) + x]
a + ex = e [(a / e) + x] = e PD ‘——– (2)
Từ (1) và (2) ta có PF / PD = e và PF ‘/ PD’ = e
Điều này cho thấy rằng một hình elip là quỹ tích của một điểm di chuyển theo cách mà tỷ số giữa khoảng cách của nó từ tiêu điểm được gọi là điểm cố định và khoảng cách của nó từ một ma trận được gọi là đường cố định bằng một hằng số e <1.
Ghi chú:
Đối với elip (x 2 / a 2 ) + (y 2 / b 2 ) = 1, ta có:
- tâm 0 (0, 0)
- Các đỉnh A (a, 0) và A ‘(- a, 0)
- Trục trục chính = 2a và trục nhỏ = 2b
- độ lệch tâm e = √1- (b 2 / a 2 )
- Các foci là F (ae, 0) và F ‘(- ae, 0)
- Phương trình của ma trận trực tiếp là x = a / e và x = -a / e
Ví dụ về Foci của một hình elip
Câu hỏi:
Tìm tọa độ các điểm của hình elip sau: x 2 + 2y 2 = 3
Giải pháp:
Được:
Phương trình elip: x 2 + 2y 2 = 3
Phương trình đã cho có thể được viết thành:
x 2/3 + y 2 / (3/2) = 1
Do đó, a = √3 và b = √ (3/2) trong đó a> b
Do đó, b 2 = a 2 (1-e 2 )
e = 1 / √2
Foci = (+ ae, 0) và (-ae, 0)
Do đó, tọa độ của các foci là: (√ (3/2), 0) và (√ (-3/2), 0)
Xem thêm: