Để có được phương trình vi phân từ phương trình này, chúng ta làm theo các bước sau: –
Bước 1 : Phân biệt hàm wrt đã cho với biến độc lập có trong phương trình.
Bước 2 : Tiếp tục phân biệt thời gian sao cho thu được (n + 1) phương trình.
Bước 3 : Sử dụng (n + 1) phương trình thu được, loại bỏ các hằng số (c 1 , c 2 ……. C n ) .
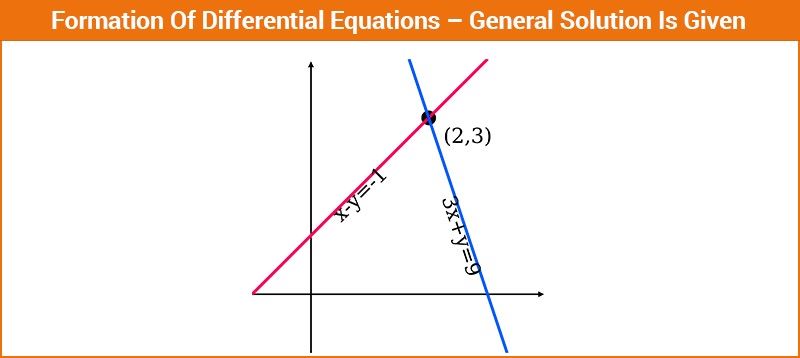
Lời giải của phương trình vi phân
Nghiệm tổng quát của phương trình vi phân là quan hệ giữa các biến x và y nhận được sau khi loại bỏ các đạo hàm (tức là tích phân) trong đó quan hệ chứa hằng số tùy ý để biểu thị bậc của một phương trình. Nghiệm của phương trình vi phân cấp một chứa một hằng số tùy ý trong khi phương trình vi phân cấp hai chứa hai hằng số tùy ý. Nếu các giá trị cụ thể được cho vào hằng số tùy ý, nghiệm tổng quát của phương trình vi phân sẽ nhận được. Để giải phương trình vi phân cấp một bậc nhất một số dạng chuẩn để có nghiệm tổng quát. Họ đang:
- Phương pháp phân tách biến
- Có thể rút gọn thành phương pháp phân tách biến
- Phương trình vi phân thuần nhất
- Phương trình vi phân không thuần nhất
- Phương trình vi phân tuyến tính
- Rút gọn thành một phương trình vi phân tuyến tính
- Phương trình vi phân chính xác
- Phương trình vi phân tuyến tính với hệ số không đổi
Chúng ta hãy xem một vài ví dụ về phương trình vi phân để hiểu rõ khái niệm này.
Ví dụ về phương trình vi phân
| Hãy làm việc:
Ví dụ 1: Tìm phương trình vi phân ứng với phương trình Y= aex+ be2 x+ ce– 3 x trong đó a, b, c là các hằng số tùy ý. Giải: Cho: y = ae x + be 2x + ce -3x y ‘= ae x + 2be 2x – 3 ce -3x y ”= ae x + 4be 2x + 9 ce -3x y ” ‘= ae x + 8be 2x – 27 ce -3x y ‘- y = được 2x – 4ce -3x ——- (1) y “- y ‘= 2be 2x + 12ce -3x ——- (2) y “’- y” = 4be 2x – 36ce -3x ——- (3) Bây giờ, với sự trợ giúp của ma trận và bằng cách sử dụng kỹ thuật loại bỏ để loại bỏ b và c, chúng ta nhận được, ⎡⎣⎢Y′– vàY” –Y′Y”′– và”124– 412– 36⎤⎦⎥= 0 Ma trận này có thể được đơn giản hóa thành, ⎡⎣⎢Y′– vàY” –Y′Y”′– và”124– 13– 9⎤⎦⎥= 0 Mở rộng chúng tôi nhận được (y’-y) (- 18-12) -1 (-9 (y ”-y ‘) – 3 (y”’ – y ”)) – 1 (4 (y” – y ‘) – 2 (y ”’- y”)) = 0 -30 (y’-y) + 5 (y ”- y ‘) + 5 (y”’ – y ”) = 0 (y ”’- y”) + (y ”- y’) – 6 (y ‘- y) = 0 y ”’ – 7y ’+ 6y = 0 d 3 y / dx 3 – 7 dy / dx + 6y = 0 Đây là phương trình vi phân cần thiết. Ví dụ 2: Tìm phương trình vi phân của tất cả các hypebol có trục nằm dọc theo cả hai trục. Giải: Phương trình chuẩn của một hyperbol là x 2 / a 2 – y 2 / b 2 = 1, có trục hoành và trục liên hợp nằm dọc theo trục tọa độ. Vì có hai hằng số tùy ý, để loại bỏ chúng, chúng ta cần phân biệt phương trình chuẩn của hyperbol hai lần. Phân biệt phương trình trên với x, chúng ta nhận được, 2x / a 2 – 2yy ‘/ b 2 = 0…. (1) 2x / a 2 = 2yy ‘/ b 2 b 2 / a 2 = yy ‘/ x … .. (2) Phân biệt (1) wrt x một lần nữa, chúng ta nhận được, 2 / a 2 – 2 / b 2 ((y ‘) 2 + yy ”) = 0 2 / a 2 = 2 / b 2 ((y ‘) 2 + yy ”) b 2 / a 2 = y ‘ 2 + yy ” …… .. (3) Cân bằng các giá trị của b 2 / a 2 từ (2) và (3) yy ‘/ x = y’ 2 + yy ” Hoặc, y (dy / dx) = x (dy / dx) 2 + xy (d 2 y / dx 2 ) Điều này đại diện cho một phương trình vi phân bậc hai thu được bằng cách loại bỏ hai tham số. Ví dụ 3: Tìm phương trình vi phân của họ đường tròn bán kính 5cm và tâm của chúng nằm trên trục x. Lời giải: Gọi tâm đường tròn trên trục x là (a, 0). Phương trình của một đường tròn như vậy có thể được cho là: (xa) 2 + y 2 = 5 2 …… (1) (xa) 2 + y 2 = 25 Phân biệt phương trình này với x, chúng ta nhận được, 2 (xa) + 2y dy / dx = 0 Lấy 2 làm phổ biến và loại bỏ, (xa) = -y (dy / dx) Thay v alue của (x – a) vào phương trình (1), ta được y 2 (dy / dx) 2 + y 2 = 25 Đây là phương trình vi phân cần thiết. |
Xem thêm:
