Hướng của một vectơ là gì? Những ví dụ dễ nhất cho người mới

Trong lĩnh vực hình học vectơ, hướng của vectơ đóng một vai trò cơ bản. Hướng của một vectơ được xác định là:

“Hướng của vectơ là hướng mà nó tác động.”

Luôn ghi nhớ tầm quan trọng của định hướng, chúng ta hãy tiến về phía trước.

Chúng tôi sẽ đề cập đến các chủ đề sau trong phần này:

• Hướng của một vectơ là gì?
• Làm thế nào để tìm hướng của một vectơ?
• Công thức tìm phương của vectơ là gì?
• Các ví dụ
• Thực hành các vấn đề

Hướng Của Vectơ Là Gì?

Vectơ là một đại lượng vật lý được mô tả bằng độ lớn và hướng. Một đại lượng vectơ được biểu diễn bằng giản đồ vectơ và do đó có hướng — hướng tại đó các điểm vectơ được xác định là hướng của vectơ. 

Theo quy ước, trong đó biểu đồ vectơ của nó biểu diễn một vectơ, hướng của nó được xác định bởi góc ngược chiều kim đồng hồ mà nó tạo với trục x dương. Theo một tỷ lệ, biểu đồ vectơ là một đường có đầu mũi tên biểu thị hướng của vectơ.

A = | A | Â

| A | đại diện cho độ lớn, và Â đại diện cho véc tơ đơn vị.

Ví dụ, để mô tả hoàn toàn vận tốc của một vật, chúng ta sẽ phải đề cập đến độ lớn và hướng của nó. Điều này có nghĩa là chúng ta sẽ phải đề cập đến tốc độ di chuyển của nó về khoảng cách tính trên một đơn vị thời gian và mô tả hướng nó đi.

Vì vậy, nếu chúng ta nói một chiếc ô tô đang chuyển động với vận tốc 40 km / giờ. Câu lệnh này chỉ mô tả tốc độ của cơ thể. Nếu ai đó nói một chiếc ô tô đang chuyển động với vận tốc 40 km / giờ và đang hướng về phía Bắc. Câu lệnh này đang mô tả vận tốc của ô tô. Nó cho chúng ta biết độ lớn mà chiếc xe đang chuyển động và hướng mà nó đang đi.

Đây là lý do tại sao, đối với chúng tôi để mô tả một vectơ, hướng cũng quan trọng như độ lớn và quan trọng. Nếu chúng ta nói rằng sôcôla nằm ngoài lớp học 3 mét về phía Bắc, nó sẽ có ý nghĩa hơn.

Chúng ta đã thấy trong ví dụ nêu trên hướng quan trọng như thế nào đối với một đại lượng vectơ.

Đầu mũi tên cho hướng của vectơ và phần đuôi biểu thị điểm hành động. Có hai cách thông thường để mô tả hướng của một vectơ.

• Hướng của vectơ có thể được mô tả bằng góc mà đuôi của nó tạo với Đông, Bắc, Tây hoặc Nam. Ví dụ, trong khi mô tả một vectơ, có thể nói rằng một vectơ hướng 80 ° Nam về phía Đông. Điều này có nghĩa là vectơ đã được quay 80 ° từ phía Đông về phía Nam. Véc tơ màu tím đại diện cho điều này.

Tương tự, một vectơ khác có thể là 65 ° Nam của Tây. Điều này có nghĩa là nó hướng 65 ° về phía đuôi từ phía Tây về phía Nam. Véc tơ màu xanh lá cây biểu thị điều này.

• Một cách khác để mô tả vectơ là theo góc quay ngược chiều kim đồng hồ từ “Đông”. Theo đó, một vectơ có hướng 50 ° sẽ hướng 50 ° từ phía Đông.

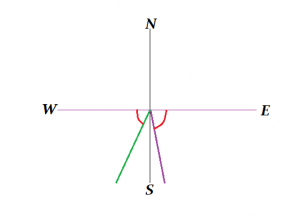
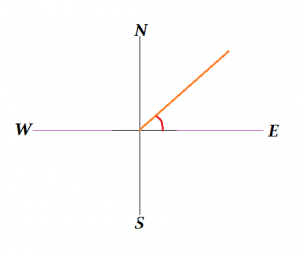
Hãy xem sơ đồ vectơ này. Nếu một vectơ được cho là có hướng 50 °. Mẹo để tìm ra nó là ghim đuôi của vectơ được căn chỉnh với trục Đông hoặc trục x. Bây giờ xoay vectơ 50 ° ngược chiều kim đồng hồ về phần đuôi của nó.

Bây giờ hãy lấy một ví dụ khác. Giả sử một vectơ có hướng là 200 °. Điều này có nghĩa là đuôi của vectơ được ghim xuống ở phía Đông và sau đó được xoay 200 ° ngược chiều kim đồng hồ.

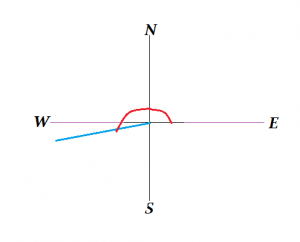
Tương tự, hệ tọa độ Hình chữ nhật cũng có thể được sử dụng. Trong trường hợp đó, góc sẽ được tính từ trục x dương.

Bây giờ, chúng ta hãy xem xét một số ví dụ để hiểu khái niệm này tốt hơn.

ví dụ 1

Vẽ một vectơ 30 ° Bắc của Tây.

Giải pháp

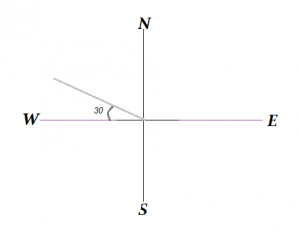
Ví dụ 2

Vẽ một vectơ có hướng 60 ° Đông Bắc.

Giải pháp

Làm thế nào để tìm hướng của một vectơ?

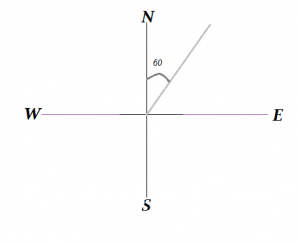
Hướng của một vectơ được xác định bởi góc của nó với đường nằm ngang. 

Có hai phương pháp tìm hướng của vectơ:

1. Phương pháp đồ họa
2. Sử dụng công thức tiếp tuyến nghịch đảo

Phương pháp đồ họa

Phương pháp đồ họa, như tên cho thấy, yêu cầu bạn vẽ vector bằng đồ thị và sau đó tính toán góc. Các bước cho phương pháp đồ họa như sau:

1. Vẽ các vectơ riêng lẻ có đuôi tại gốc và theo các góc của chúng.
2. Sử dụng quy tắc head-to-tail, thêm các vectơ.
3. Các vector kết quả R được định hướng từ đuôi của vector đầu tiên Một người đứng đầu các vector thứ hai B .
4. Độ lớn và hướng của vectơ sau đó được xác định bằng cách sử dụng thước kẻ và thước đo góc. Độ dài của vectơ kết quả R sẽ cung cấp cho nó độ lớn.
5. Đối với phương hướng, vẽ một đường song song với trục x đi qua điểm bắt đầu của vector kết quả R . Đo góc giữa đường ngang và kết quả.

Tuy nhiên, đây là vấn đề: Phương pháp này chỉ dành cho những hiểu biết cơ bản. Sẽ phức tạp nếu bạn phải thêm nhiều vectơ và không phải lúc nào cũng cho kết quả chính xác nhất. Luôn có cơ hội do lỗi của con người. Do đó, chúng tôi có phương pháp thứ hai:

Công thức tiếp tuyến nghịch đảo 

Chúng ta sử dụng hàm tiếp tuyến nghịch đảo để tìm góc của nó với đường nằm ngang .

Điều này có thể thực hiện được nếu bạn có tọa độ ban đầu và điểm tọa độ cuối cùng của một vectơ trong một mặt phẳng. Nó được đưa ra bởi:

θ = tan-1 (y / x)

Ví dụ 3

Một vectơ được hướng từ điểm gốc đến (3,5). Xác định hướng của nó.

Giải pháp

Ở đây chúng ta có thể thấy rằng,

a = x = 3

b = y = 5

θ = tan-1 (a / b)

θ = tan-1 (3/5)

θ = 30,9 °

Vectơ hướng 30,9 ° so với trục x.

Bây giờ, hãy xem xét một trường hợp mà đuôi không nằm ở điểm gốc, mà là vectơ được đặt ở một nơi khác trong mặt phẳng. Trong trường hợp này, công thức được sửa đổi như sau:

Theo tài sản Pythagore, chúng ta biết:

tanθ = Δy / Δx

tanθ = (y2 – y1) / (x2 – x1)

θ = tan-1 (y2 – y1) / (x2 – x1)

Vì vậy, công thức được sửa đổi thành:

θ = tan-1 (y1 – y0) / (x1 – x0)

Góc cho bởi nó là từ đường nằm ngang, chạy song song với trục x.

Hãy giải một số ví dụ để hiểu khái niệm này.

Ví dụ 4

Tìm hướng của vectơ nằm từ A (2,1) đến B (6,9)

Δx = x1 – x0 = 6 -2 = 4

Δy = y1 – y0 = 9 -1 = 8

Giải pháp

Sử dụng công thức:

θ = tan-1 (y1 – y0) / (x1 – x0)

θ = tan-1 (8/4)

θ = 63,4 °

Các quy ước về hướng của một vectơ

Hãy chuyển sang một trường hợp khó hơn nhiều.

Chúng ta đã thấy rằng trong ví dụ trên, vectơ nằm trong Góc phần tư thứ nhất. Hãy xem nó hoạt động như thế nào đối với phần còn lại của Phần tư. Điều này có thể được xác định bởi các dấu hiệu của tọa độ của vectơ, xác định góc phần tư trong đó góc nằm.

Đối với điều này, cần tuân thủ một số quy ước nhất định:

1. Nếu cả hai tọa độ đều dương thì góc tồn tại trong góc phần tư thứ nhất và được coi là góc chuẩn. θ = Ⲫ
2. Nếu tọa độ y dương nhưng tọa độ x âm thì góc tồn tại trong góc phần tư thứ 2 thì góc chuẩn là: θ = 180 + Ⲫ
3. Nếu cả hai tọa độ đều âm thì góc tồn tại trong góc phần tư thứ 3 thì góc chuẩn là: θ = 270 + Ⲫ
4. Nếu tọa độ x dương nhưng tọa độ y âm thì góc chuẩn là: θ = 360 + Ⲫ.

Hãy dưới đây với sự trợ giúp của các ví dụ.

Ví dụ 5

Tìm phương của một vectơ có hướng từ gốc tọa độ (6, -7).

Giải pháp

Chúng tôi sẽ trợ giúp từ công thức tiếp tuyến nghịch đảo:

θ = tan-1 (-7/6)

θ = -49,23 °

Ở đây chúng ta có thể thấy từ tọa độ của vectơ mà nó nằm trong Góc phần tư IV.

Bây giờ, đây là thỏa thuận:

Công thức cho góc ngắn nhất từ ​​trục x dương hoặc âm. Quy ước là biểu diễn góc có dấu dương tính từ trục x dương. Đối với điều này, chúng tôi trừ 360 ° cho góc thu được.

θ ‘= -49,23 + 360

θ = 310,77 °

Ví dụ 6

Tìm phương của vectơ (-4,3).

Giải pháp

Bằng cách nhìn vào tọa độ, chúng ta biết rằng vectơ nằm trong Góc phần tư II:

θ = tan-1 (3 / -4)

θ = -36,87 °

Đây là góc từ trục x âm. Bây giờ, để có câu trả lời khẳng định và được tính từ trục x dương ngược chiều kim đồng hồ:

θ = -36,87 + 180

θ = 143,13 °

từ trục x dương theo chiều ngược chiều kim đồng hồ.

Xem thêm:

Góc giữa hai Vectơ – Giải thích và Ví dụ

Hình học Vectơ – Giải thích & Ví dụ dễ hiểu nhất

Để tìm ra hướng của vectơ kết quả

Tiếp tục, hãy xem làm thế nào chúng ta có thể tìm thấy hướng của kết quả của hai hoặc nhiều vectơ.

Như bạn đã biết, để tính vectơ kết quả của hai hoặc nhiều vectơ riêng lẻ, trước tiên chúng ta tìm tọa độ hình chữ nhật tương ứng của chúng. Tiếp theo, chúng ta thêm thành phần x và thành phần y của hai vectơ. Trên thực tế, thành phần x và thành phần y là các thành phần của vectơ kết quả.

Sau đây là bước để tính toán hướng của một kết quả của hai hoặc nhiều vectơ:

Giả sử bạn có vectơ A và B, và bạn muốn tìm kết quả và hướng của chúng.

1. Hòa tan cả hai vectơ thành các thành phần hình chữ nhật của chúng.
2. Ta biết, R = A + B. Tương tự, Rₓ = Aₓ + Bₓ và R𝚢 = A𝚢 + B𝚢
3. Bây giờ sử dụng thuộc tính tiếp tuyến nghịch đảo, thay thế x và y bằng x, y-các thành phần của kết quả, tức là, = ta n -1 (Ry / Rx)
4. Xác định góc phần tư của kết quả và sửa đổi theta theo nó.

Vấn đề thực hành 

1. Tìm phương của một vectơ có điểm đầu và điểm cuối lần lượt là (5, 2) và (4, 3).
2. Tìm phương của một vectơ có điểm ban đầu và điểm cuối lần lượt là (2, 3) và (5, 8).
3. Một vectơ có hướng từ điểm gốc đến (7, 4). Tìm hướng của nó.
4. Tìm phương của một vectơ có tọa độ là (-7, -5).
5. Tìm phương của một vectơ có tọa độ là (1, -1).

Câu trả lời

1. -45 ° hoặc 135 °
2. 59 °
3. 29,74 °
4. 234 °
5. -45 ° hoặc 135 °