Vectơ song song và những điều bạn chưa biết

Phép nhân vô hướng cho kết quả là các vectơ song song. Đây là các vectơ:

“Có cùng hướng hoặc ngược chiều và là bội số vô hướng của nhau.”

Trong chủ đề này, chúng ta sẽ thảo luận về các khía cạnh quan trọng sau đây của vectơ song song:

• Vectơ song song là gì?
• Làm thế nào để xác định xem hai vectơ là song song.

Vectơ song song là gì? 

Thông thường, hai vectơ song song là bội số vô hướng của nhau. Giả sử hai vectơ, a và b, được định nghĩa là:

b = c * a

Trong đó c là một số thực vô hướng nào đó. Trong phương trình trên, vectơ b được biểu diễn dưới dạng bội vô hướng của vectơ a, và hai vectơ được cho là song song. Dấu của vô hướng c sẽ xác định hướng của vectơ b. Nếu giá trị của c dương, c> 0 thì cả hai vectơ sẽ có cùng phương. Nếu giá trị của c âm, tức là c <0, vectơ b sẽ hướng ngược hướng với vectơ a.

Tương tự, từ phương trình trên, vectơ a có thể được biểu diễn thành:

a = 1 / c * b

Như vậy, rõ ràng chúng phải là bội số vô hướng của nhau để hai vectơ bất kỳ song song. Hãy xem xét trường hợp giá trị của c bằng không. Sau đó, chúng ta có thể viết:

b = 0 * a

b = 0

Trong trường hợp này, vectơ b trở thành vectơ không và vectơ 0 được coi là song song với mọi vectơ.

Cách xác định xem hai vectơ có song song không

Để xác định xem hai vectơ có song song hay không, chúng ta kiểm tra xem các vectơ đã cho có thể được biểu diễn dưới dạng bội vô hướng của nhau hay không. Ví dụ, hai vectơ U và V song song nếu tồn tại một số thực, t, sao cho:

U = t * V

Số này, t, có thể là số dương, số âm hoặc số không.

Các ví dụ

Trong phần này, chúng ta sẽ thảo luận về các ví dụ liên quan đến vectơ song song và các giải pháp từng bước của chúng. Điều này sẽ giúp hiểu sâu hơn về vectơ song song.

ví dụ 1 

Một ô tô đang chuyển động với vectơ vận tốc V1 = 30 m / s hướng Bắc, ô tô khác chuyển động hướng Bắc với vectơ vận tốc V2 = 60 m / s. Xác định xem hai vectơ vận tốc có song song hay không.

Giải pháp

Chúng tôi có thông tin sau:

V1 = 30 m / s, hướng Bắc

V2 = 60 m / s, hướng Bắc

Để xác định xem các vectơ đã cho có song song hay không, chúng ta kiểm tra xem chúng có thể được biểu diễn dưới dạng bội số của nhau hay không. Chúng ta có thể liên hệ hai vectơ như sau:

    V2 = 2 * (30 m / s)

V2 = 2 * V1

V2 = 2 * (30 m / s)

Hoặc là,

V1 = 1/2 * V1

V1 = 1/2 * (60 m / s)

V1 = 30 m / s.

Vì các vectơ đã cho có thể liên hệ với nhau theo hệ số vô hướng bằng 2 hoặc 1/2, nên ta có thể kết luận rằng hai vectơ vận tốc V1 và V2 song song với nhau.

Ví dụ 2

Cho hai vectơ S1 = (2, 3) và S2 = (10, 15), xác định xem hai vectơ đó có song song hay không. Sau đó, xác định độ lớn của hai vectơ.

Giải pháp

Các vectơ S1 và S2 đã cho được biểu diễn dưới dạng cột. Để xác định xem chúng hay song song, chúng ta có thể kiểm tra xem các thành phần tương ứng của chúng có thể được biểu diễn dưới dạng bội số vô hướng của nhau hay không.

S2 = (5 * 2, 5 * 3)

S2 = 5 * (2, 3)

S2 = 5 * S1

Hoặc là,

S1 = 1/5 * S2

Rõ ràng từ các phương trình trên rằng các vectơ S1 và S2 là bội số vô hướng của nhau và hệ số tỉ lệ là 5 hoặc 1/5. Do đó, các vectơ đã cho song song với nhau.

Bây giờ, chúng ta có thể tính toán độ lớn của các vectơ đã cho như sau:

| S1 | = √2 ^ 2 + 3 ^ 2

| S1 | = √4 + 9

| S1 | = √13

Độ lớn của vectơ S2 là:

| S2 | = √10 ^ 2 + 15 ^ 2

| S2 | = √100 + 225

| S2 | = √325

| S2 | = √25 * 13

| S2 | = 5 * √13

Độ lớn của hai vectơ cũng liên quan bởi các hệ số tỉ lệ.

Ví dụ 3

Cho hai vectơ P = (4, 6) và Q = (-2, -3), xác định xem hai vectơ đó có song song hay không.

Giải pháp

Các vectơ P và Q đã cho được biểu diễn dưới dạng cột. Để xác định xem chúng hay song song, chúng ta có thể kiểm tra xem các thành phần tương ứng của chúng có thể được biểu diễn dưới dạng bội số vô hướng của nhau hay không.

P = (4, 6)

Q = (-2, -3)

P = -2 (-2, -3)

P = -2 * Q

Kể từ khi vector P là -2 lần so với vector Q , hai vectơ song song với nhau, và sự chỉ đạo của vector Q là đối diện với sự chỉ đạo của vector P .

Ví dụ 4

Tham khảo hình ảnh cho dưới đây và xác định các vectơ song song.

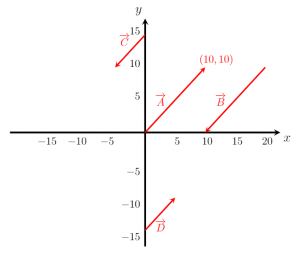
Giải pháp

Tất cả bốn vectơ được hiển thị trong hình ảnh đều song song với nhau vì chúng có thể được biểu diễn dưới dạng bội số vô hướng của các vectơ khác.

Để xác minh điều này, hãy biểu thị các vectơ ở dạng cột của chúng dưới dạng:

A = (10,10) , vectơ B = (-10, -10), C = (-5, -5) và D = (5, 5)

Đầu tiên, chúng ta kiểm tra xem các vectơ A và B có song song hay không.

Rõ ràng, vectơ B có thể được biểu diễn dưới dạng:

B = (-10, -10)

B = -1 * (10,10)

Hoặc là,

B = -1 * A

Do đó, các vectơ A và B song song với nhau.

Tiếp theo, chúng tôi kiểm tra các vectơ C và D là:

D = (5, 5)

C = -1 * (5,5)

C = -1 * D

Các vectơ C và D cũng là bội số vô hướng của nhau.

Tương tự, chúng tôi kiểm tra mối quan hệ giữa các vectơ còn lại:

B = 2 * C

B = – 2 * D

C = – 2 * A

D = 2 * A

Như vậy, từ các phương trình ở trên và hình ảnh nhất định, nó là rõ ràng rằng tất cả bốn vectơ, Một , B , C, và D, song song với nhau.

Ví dụ 5

Cho biết các vectơ A = (-4, 6) và B = (x, 12) là các vectơ song song, hãy xác định giá trị của x.

Giải pháp

Vì các vectơ song song nên chúng ta biết rằng:

B = c * A

Trong đó c là một giá trị vô hướng nào đó. Việc thay thế các giá trị của các vectơ cho chúng ta:

(x, 12) = c * (-4, 6)

(x, 12) = (-4c, 6c)

Bằng cách đặt các giá trị thành phần riêng lẻ bằng nhau, chúng tôi nhận được:

x = -4c

12 = 6c

Đơn giản hóa các phương trình trên cho chúng ta:

c = 2

Nếu chúng ta đặt giá trị của c vào phương trình khác và đơn giản hóa, chúng ta có:

x = -4 * 2

x = -8

Do đó, vectơ B trở thành:

B = (-8, 12).

Ví dụ 6

Cho vectơ m = 5i + 6j +3 trong hệ trực giao, hãy xác định một vectơ song song với vectơ này và hướng ngược lại.

Giải pháp

Hãy coi một vectơ n là một vectơ song song với vectơ m đã cho. Vectơ n có thể được biểu diễn dưới dạng:

n = k * m

n = k * (5i + 6j +3)

Trong đó k là bội số vô hướng của vectơ m. Ngoài ra, k có thể là số dương, số âm hoặc số không. Vì người ta đã xác định rằng vectơ đã cho phải hướng ngược hướng với hướng của m nên k phải không dương. Tức là, k <0. Nếu k = -3 và chúng ta nhận được:

n = -3 * (5i + 6j +3)

n = ((-3 * 5i + (-3 * 6j) + (-3 * 3))

n = -15i -18j -9

Vectơ kết quả n song song với vectơ đã cho và ngược hướng, mặc dù có vô số vectơ đáp ứng tiêu chí này.

Xem thêm:

Kiến thức mới nhất về Vectơ kết quả

Cách giải Vectơ Phủ định nhanh chóng chi tiết nhất

Câu hỏi thực hành 

1. Cho vectơ M = 10 m, Đông và vectơ thứ hai, 3 M, Tây . Xác định xem hai vectơ có song song hay không.
2. Cho vectơ N = 15 m North, xác định vectơ kết quả thu được bằng cách nhân vectơ đã cho với -4. Sau đó, kiểm tra xem hai vectơ có song song với nhau hay không.
3. Gọi u = (-1, 4) và v = (n, 20) là hai vectơ song song. Xác định giá trị của n.
4. Cho v = (3, 9). Tìm 1/3 v và kiểm tra xem hai vectơ có song song hay không.
5. Cho vectơ b = -3i + 2j +2 trong hệ trực giao, hãy tìm một vectơ song song.
6. Cho a = (1, 2), b = (2, 3) và c = (2,4). Xác định xem các vectơ đã cho có song song với nhau hay không.

Câu trả lời

1. 3 M = 30 m, hướng Tây. Rõ ràng, các vector mới song song với vector M , nhưng hướng của nó là đối diện của vector M .
2. -4 N = -60 m. Hướng là nam. Hai vectơ thực sự song song với nhau.
3. u = k * v , trong đó k = 1/5 và n = -5, v = (-5, 20). Phương của u và v không đổi.
4. 1/3 v = (1, 3), | v | = 3 * √10, | 1/3 v | = √10. Hướng của vectơ 1/3 v trùng với hướng của vectơ v và hai vectơ song song với nhau.
5. 5 b = -15i + 10j + 10 là một trong vô số vectơ song song với b .
6. Các vectơ a và c song song với nhau, nhưng vectơ b không song song với một trong hai vectơ còn lại.