Khối lượng hình nón được tính như nào? Công thức tính dễ hiểu nhất

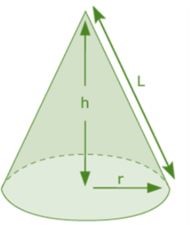
Trong hình học, hình nón là một hình 3 chiều có đáy là hình tròn và mặt cong thuôn nhọn từ đáy đến đỉnh hoặc đỉnh ở đỉnh. Nói một cách dễ hiểu, hình nón là một hình chóp có đáy là hình tròn.

Các ví dụ phổ biến về hình nón là hình nón kem, hình nón giao thông, hình phễu, tipi, tháp pháo lâu đài, đỉnh đền thờ, đầu bút chì, loa phóng thanh, cây thông Noel, v.v.

Trong bài này, chúng ta sẽ thảo luận về cách sử dụng thể tích của một công thức hình nón để tính thể tích của một hình nón.

Làm thế nào để Tìm khối lượng của một hình nón?

Trong một hình nón, độ dài vuông góc giữa đỉnh của hình nón và tâm của hình tròn được gọi là chiều cao ( h ) của hình nón . Chiều dài nghiêng của hình nón là số đo chiều dài ( L ) của hình nón dọc theo mặt cong hình côn. Tất cả các thông số này được đề cập trong hình trên.

T o tìm thể tích của một hình nón, bạn cần, các thông số sau:

• Bán kính( r ) của đáy hình tròn,
• Chiều cao hoặc chiều cao nghiêng của hình nón.

Giống như tất cả các thể tích khác, thể tích của một hình nón cũng được biểu thị bằng đơn vị khối.

Thể tích của một công thức hình nón

Thể tích của một hình nón bằng một phần ba tích của diện tích đáy và chiều cao. Công thức cho khối lượng được biểu diễn như sau:

Thể tích khối nón = ⅓ x πr ²  xh

V = ⅓ πr ² giờ

Trong đó V là thể tích, r là bán kính và h là chiều cao.

Chiều cao nghiêng, bán kính và chiều cao của một hình nón liên quan đến;

Chiều cao nghiêng của hình nón, L = √ (r ² + h ² ) ………. (Định lý Pythagore)

Chúng ta hãy tìm hiểu sâu hơn về thể tích của một công thức hình nón bằng cách giải ra một vài bài toán ví dụ.

ví dụ 1

Tìm thể tích của hình nón có bán kính 5 cm và chiều cao 10 cm.

Giải pháp

Theo thể tích của một công thức hình nón, chúng ta có,

⇒V = ⅓ πr ² giờ

⇒V = ⅓ x 3,14 x 5 x 5 x 10

= 262 cm ³

Ví dụ 2

Bán kính và chiều cao nghiêng của hình nón là 12 mm và 25 mm. tương ứng. Tìm thể tích của khối nón.

Giải pháp

Được:

Chiều cao nghiêng, L = 25 mm

bán kính, r = 12 mm

L = √ (r ² + h ² )

Bằng cách thay thế, chúng tôi nhận được,

⇒25 = √ (12 ² + h ² )

⇒25 = √ (144 + giờ ² )

Hình vuông cả hai bên

⇒625 = 144 + giờ ²

Lấy cả hai bên trừ đi 144.

481 = giờ ²

√481 = h

h = 21,9

Do đó, chiều cao của hình nón là 21,9 mm.

Bây giờ, hãy tính toán khối lượng.

Khối lượng = ⅓ πr ² giờ

= ⅓ x 3,14 x 12 x 12 x 21,9

= 3300,8 mm ³ .

Ví dụ 3

Một silo hình nón có bán kính 9 feet và cao 14 feet giải phóng ngũ cốc ở đáy của nó với tốc độ không đổi 20 feet khối mỗi phút. Mất bao lâu để silo trống?

Giải pháp

Đầu tiên, hãy tìm thể tích của silo hình nón

Thể tích = ⅓ x 3,14 x 9 x 9 x 14

= 1186,92 feet khối.

Để có thời gian cho silo rỗng, hãy chia thể tích của silo cho tốc độ dòng chảy của ngũ cốc.

= 1186,92 feet khối / 20 feet khối mỗi phút

= 59 phút

Ví dụ 4

Một bể chứa hình nón có đường kính 5 m, cao 10 m. Tìm dung tích của bể theo lít.

Giải pháp

Cho trước, đường kính = 5 m ⇒ bán kính = 2,5 m

Chiều cao = 10 m

Thể tích khối nón = ⅓ πr ² h

= ⅓ x 3,14 x 2,5 x 2,5 x 10

= 65,4 m ³

Vì 1000 lít = 1 m ³ , thì

65,4 m ³ = 65,4 x 1000 lít

= 65400 lít.

Ví dụ 5

Một quả cầu đặc bằng nhựa có bán kính 14 cm bị nung chảy thành một hình nón có chiều cao là 10 cm. Bán kính của hình nón sẽ là bao nhiêu?

Giải pháp

Thể tích khối cầu = 4/3 πr ³

= 4/3 x 3,14 x 14 x 14 x 14

= 11488,2 cm ³

Hình nón cũng sẽ có cùng thể tích là 11488,2 cm ³

Vì thế,

⅓ πr ² h = 11488,2 cm ³

⅓ x 3,14 xr ² x 10 = 11488,2 cm ³

10,5r ² = 11488,2 cm ³

r ² = 1094

r = √1094

r = 33

Do đó, bán kính của hình nón sẽ là 33 cm.

Ví dụ 6

Tìm thể tích của hình nón có bán kính là 6 feet và chiều cao là 15 feet

Giải pháp

Thể tích hình nón = 1/3 x 3,14 x 6 x 6 x 15

= 565,2 ft ³ .

Xem thêm:

Tính khối lượng của khối nhanh gọn dễ hiểu nhất 2021

Các bước tính khối lượng của Lăng kính siêu đơn giản