Hướng dẫn phép cộng vectơ nhanh chóng, dễ hiểu nhất

Giống như phép cộng vô hướng, phép cộng vectơ liên quan đến việc đặt hai hoặc nhiều vectơ lại với nhau. Cụ thể hơn, khi bạn thêm vectơ, bạn sẽ:

“Thêm hai hoặc nhiều vectơ bằng cách sử dụng phép toán cộng để nhận được một vectơ mới bằng tổng của hai hoặc nhiều vectơ.”

Trong chủ đề này, chúng ta sẽ thảo luận về phép cộng vectơ từ các khía cạnh sau:

• Phép cộng vectơ là gì?
• Cách thêm vectơ bằng đồ họa
• Cách thêm hai vectơ

Phép cộng vectơ là gì?

Hai vectơ A và B có thể được cộng với nhau bằng phép cộng vectơ và vectơ kết quả có thể được viết dưới dạng:

QUẢNG CÁO

R = A + B

Cách thêm vectơ bằng đồ họa

Chúng ta phải xem xét cả hai thành phần của một vectơ, đó là hướng và độ lớn khi sử dụng phép cộng vectơ.

Hãy nhớ rằng hai vectơ có cùng độ lớn và hướng có thể được thêm vào giống như vô hướng.

Trong chủ đề này, chúng ta sẽ khám phá các phương pháp đồ họa và toán học của phép cộng vectơ, bao gồm:

1. Phép cộng vectơ sử dụng quy tắc từ đầu đến đuôi
2. Phép cộng vectơ bằng phương pháp hình bình hành
3. Thêm vectơ bằng cách sử dụng các thành phần

Phép cộng vectơ sử dụng quy tắc từ đầu đến đuôi

Phép cộng vectơ có thể được thực hiện bằng phương pháp head-to-tail nổi tiếng. Theo quy tắc này, hai vectơ có thể được cộng lại với nhau bằng cách đặt chúng lại với nhau sao cho phần đầu của vectơ thứ nhất nối với phần đuôi của vectơ thứ hai. Sau đó có thể thu được vectơ tổng kết quả bằng cách nối đuôi của vectơ đầu tiên với đầu của vectơ thứ hai. Phương pháp này đôi khi còn được gọi là phương pháp cộng véc tơ tam giác.

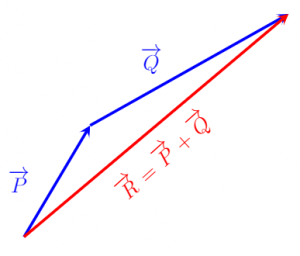
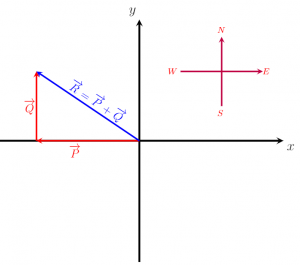
Phép cộng vectơ bằng cách sử dụng quy tắc đầu đến đuôi được minh họa trong hình ảnh bên dưới. Hai vectơ P và Q được thêm vào bằng phương pháp đầu-đuôi, và chúng ta có thể thấy tam giác được tạo thành bởi hai vectơ gốc và vectơ tổng.

Thứ nhất, hai vectơ P và Q được xếp cạnh nhau như vậy mà đầu của vector P nối đuôi của vector Q . Tiếp theo, để tìm ra Tóm lại, một vector kết quả R được vẽ như vậy mà nó kết nối đuôi của P cho người đứng đầu của Q .

Về mặt toán học, tổng hoặc kết quả, vectơ, R, trong hình ảnh dưới đây có thể được biểu thị như sau:

R   = P + Q

Phép cộng vectơ bằng phương pháp hình bình hành

Để hiểu phép cộng vectơ bằng phương pháp hình bình hành, chúng ta sẽ xem xét và giải thích hình bên dưới.

Đầu tiên, vẽ các vectơ đã cho, A và B, có cùng điểm ban đầu như trong hình dưới đây. Sau đó, vẽ một hình bình hành bằng cách sử dụng bản sao của các vectơ đã cho.

Thứ hai, vẽ các bản sao của vector B gọi là B’, và đặt nó song song với vector B để kết nối  với người đứng đầu của vector đầu tiên, Một . Tương tự, vẽ một bản sao của vectơ A được gọi là A ‘, và đặt nó song song với A sao cho phần đuôi của nó nối với phần đầu của vectơ B.

Cuối cùng, kết quả của hai vectơ, bằng tổng các vectơ A và B , sẽ là đường chéo của hình bình hành. Nó có thể được vẽ bằng cách nối điểm đầu của hai vectơ A và B với điểm đầu của vectơ A ‘ và B’ .

Tóm lại, cần có ba bước để thực hiện phép cộng vectơ bằng phương pháp hình bình hành:

Bước 1: Đặt hai vectơ sao cho chúng có điểm xuất phát chung

Bước 2: Vẽ và hoàn thành hình bình hành bằng cách sử dụng bản sao của hai vectơ ban đầu

Bước 3: Đường chéo của hình bình hành khi đó bằng tổng của hai vectơ

Thêm vectơ bằng cách sử dụng các thành phần

Như chúng ta đã biết, các vectơ cho trong hệ tọa độ Descartes có thể được phân tách thành các thành phần ngang và dọc của chúng. Ví dụ, một vectơ P ở góc Φ, như thể hiện trong hình dưới đây, có thể được phân tách thành các thành phần của nó như:

P _x , đại diện cho thành phần của vectơ P dọc theo trục hoành (trục x), và

P _y , đại diện cho thành phần của vectơ P dọc theo trục tung (trục y).

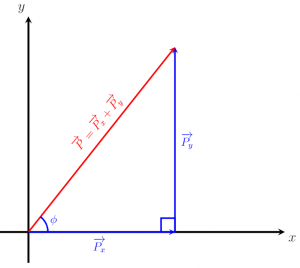
Có thể thấy rằng ba vectơ tạo thành một tam giác vuông và vectơ P có thể được biểu thị là:

P =  P _x + P _y

Về mặt toán học, các thành phần của vectơ cũng có thể được tính toán bằng cách sử dụng độ lớn và góc của vectơ đã cho.

P _{x =} P cos Φ

P _{y =} P sin Φ

Hơn nữa, chúng ta cũng có thể xác định vectơ kết quả nếu các thành phần ngang và dọc của nó được đưa ra. Ví dụ, nếu các giá trị của P _x   và P _y  được cho trước, thì chúng ta có thể tính độ lớn và góc của vectơ P như sau:

| P | =  √ (P _x ) ^ 2 + (P _y ) ^ 2

Và góc có thể được tìm thấy là:

Φ = tan ^-1 (P _y / P _x )

Vì vậy, tóm lại, chúng ta có thể xác định một vectơ kết quả nếu các thành phần của nó được cho trước. Ngoài ra, nếu véc tơ chính nó đã cho, chúng ta có thể xác định các thành phần bằng cách sử dụng các phương trình trên.

Tương tự, nếu các vectơ được biểu diễn trong các cặp có thứ tự (vectơ cột), chúng ta có thể thực hiện phép cộng trên các vectơ bằng cách sử dụng các thành phần của chúng. Ví dụ, coi hai vectơ M và N là:

M = (m1, m2)

N = (n1, n2)

Thực hiện phép cộng vectơ trên hai vectơ tương đương với việc cộng thành phần x và y tương ứng của hai vectơ. Điều này tạo ra vectơ kết quả S :

S = M + N

S = (m1 + n1, m2 + n2).

Nó có thể được viết rõ ràng là:

Sx = m1 + n1

Sy = m2 + n2.

Độ lớn của vectơ kết quả S có thể được tính như sau:

| S | =  √ (S _x ) ^ 2 + (S _y ) ^ 2

Và góc có thể được tính là:

Φ = tan ^-1 (S _y / S _x ).

Cách thêm hai vectơ

Phần này sẽ thảo luận về các ví dụ về phép cộng vectơ và các giải pháp từng bước của chúng để có một số thực hành bằng cách sử dụng các phương pháp khác nhau đã thảo luận ở trên.

Các ví dụ

ví dụ 1

Cho rằng hai vectơ, A và B, như được hiển thị trong hình dưới đây, xác định tổng của chúng bằng đồ thị bằng cách sử dụng phương pháp đầu-đuôi.

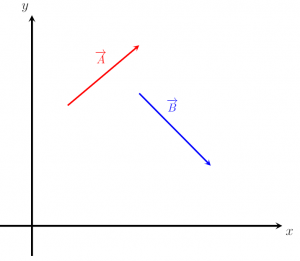
Giải pháp

Bước đầu tiên của phương pháp head-to-tail là đặt các vectơ A và B đã cho sao cho đuôi của vectơ B nối với đầu của vectơ A, như thể hiện trong hình dưới đây. Tiếp theo, để tìm số tiền của họ, chúng tôi rút ra một vector kết quả R để nó kết nối đuôi của vector Một người đứng đầu vector B . Về mặt toán học, kết quả có thể được biểu thị như sau:

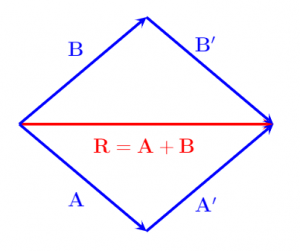
R = A + B

Ví dụ 2

Cho hai vectơ, AB = (3, 2) và BC = (2, 2), xác định tổng của chúng bằng cách sử dụng quy tắc đầu-đuôi.

Giải pháp

AB + BC = (3, 2) + (2, 2)

AB + BC = (3 + 2, 2 + 2)

AB + BC = (5, 4).

Hoặc như thể hiện trong hình ảnh bên dưới, vectơ kết quả có thể được viết là:

AC = (5, 4)

Lưu ý: Để sử dụng quy tắc tam giác / quy tắc đầu đến đuôi, chữ cái trung gian của hai vectơ được thêm vào phải giống nhau:

AC = AB + BC

Trong ví dụ này, chữ trung gian là B .

Độ lớn của vectơ kết quả AC có thể được tìm thấy như sau:

| AC | = √ (AC _x ) ^ 2 + (AC _Y ) ^ 2

| AC | = √ (5) ^ 2 + (4) ^ 2

| AC | = √ 25 + 16

| AC | = 6.403 đơn vị (gần đúng).

Góc của vectơ kết quả AC có thể được tìm thấy như sau:

Φ = tan ^-1 (AC _y / AC _x )

Φ = tan ^-1 (4/5)

Φ = tan ^-1 (4/5)

Φ = 38,66 độ

Ví dụ 3

Cho hai vectơ, S = 10 m, Φ = 30 độ và T = 20m, Φ = 60 độ, hãy xác định tổng của chúng. Sau đó, tính độ lớn và góc của vectơ kết quả bằng phương pháp thành phần.

Giải pháp

Gọi R là vectơ kết quả bằng tổng các vectơ đã cho, có thể được biểu diễn dưới dạng:

R = S + T

Để sử dụng phương thức thành phần, trước tiên chúng ta xem xét các phần thành phần của các vectơ đã cho. Thành phần nằm ngang của S là:

Sx = S Cos Φ

Sx = 10 Cos 30

Sx = 8.660 m (Khoảng)

Tương tự, đối với thành phần dọc:

Sy = S Sin Φ

Sy = 10 Sin 30

Sy = 5 m

Tiếp theo, chúng tôi tính toán các thành phần của vectơ T:

Tx = T Cos Φ

Ty = T Sin Φ

Ở đâu,

Tx = 20 Cos 60

Tx = 10m

Ty = 20 Sin 60

Ty = 17.320 (xấp xỉ)

Bây giờ, chúng ta có thể tính toán vectơ tổng bằng cách thêm các thành phần x và y riêng lẻ của vectơ S và T như sau:

Rx = Sx + Tx

Rx = 8,660 + 10

Rx = 16,660 m

Ry = Sy + Ty

Ry = 5 + 17,32

Ry = 22.320 m

Vectơ kết quả R có thể được biểu diễn ở dạng cột như sau:

R = (16,66, 22,32).

Cuối cùng, độ lớn và góc của vectơ kết quả có thể được tìm thấy là:

| R | = √ (16,66) ^ 2 + (22,32) ^ 2

| R | = 23,292 m (Khoảng)

Φ = tan ^-1 (Ry / Rx)

Φ = tan ^-1 (22,32 / 16,66)

Φ = 53,26 độ (Khoảng)

Do đó, vectơ tổng kết quả là:

R = 23,292 m, Φ = 53,26 độ.

Ví dụ 4

Một du khách đi thẳng về hướng Tây với P = 20 m rồi đến Q = 10 m đi thẳng về hướng Bắc. Xác định xem khách du lịch cách điểm xuất phát bao xa. Ngoài ra, cung cấp độ lớn và góc của vectơ kết quả.

Giải pháp

Đầu tiên, chúng tôi biểu diễn bằng đồ thị các vectơ chuyển vị đã cho P và Q và sau đó vẽ vectơ kết quả của chúng bằng cách sử dụng quy tắc đầu đến đuôi, như thể hiện trong hình dưới đây. Rõ ràng từ hình ảnh mà các du khách bao phủ một khoảng cách tương đương với độ lớn của vector R từ điểm khởi đầu.

Bây giờ, để tính toán toán học vectơ kết quả, chúng tôi sử dụng các công thức sau:

R = P + Q

| R | = √ (20) ^ 2 + (10) ^ 2

| R | = 22,36 m (Khoảng)

Và góc có thể được tính là:

Φ = tan ^-1 (10/20)

Φ = 26,57 độ

Do đó, du khách đã đi được khoảng cách 22,36 m từ điểm xuất phát ở một góc 26,57 độ về phía tây bắc.

Ví dụ 5

Xác định vectơ tổng kết quả của hai vectơ A = (-5, -1) và B = (2, -1).

Giải pháp

Các vectơ đã cho đã ở dạng thành phần của chúng, vì vậy trước tiên chúng ta xác định góc của chúng.

Đối với vectơ A:

Φ = tan ^-1 (Ay / Ax)

Φ = tan ^-1 (-1 / -5)

Φ = 11,31 độ.

Đối với vectơ B:

Φ = tan ^-1 (Theo / Bx)

Φ = tan ^-1 (-1/2)

Φ = -26,57 độ.

Tiếp theo, chúng tôi tìm vectơ kết quả bằng cách thêm các thành phần riêng lẻ:

S = A + B

Sx = Ax + Bx

Sx = -5 + 2

Sx = -3

Sy = Ay + By

Sy = -1 -1

Sy = -2

Vectơ kết quả S có thể được biểu thị dưới dạng vectơ cột:

S = (-3, -2).

Cuối cùng, độ lớn và góc của vectơ kết quả là:

| S | = √ (-3) ^ 2 + (-2) ^ 2

| S | = 3,605 đơn vị (Khoảng)

Φ = tan ^-1 (Sy / Sx)

Φ = tan ^-1 (-2 / -3)

Φ = 33,69 độ

Do đó, vectơ tổng kết quả là:

S = 3,605 đơn vị, Φ = 33,69 độ.

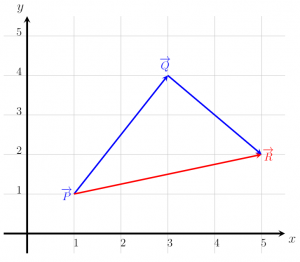
Ví dụ 6

Cho hai vectơ PQ  và QR, như trong hình dưới đây, hãy tính giá trị tổng của chúng, vectơ PR .

Giải pháp

Từ hình ảnh đã cho, vectơ kết quả có thể được đưa ra là:

PQ + QR = (2, 3) + (2, -2)

PQ + QR = (4, 1).

Nó cũng có thể được viết là:

PR = (4, 1)

Độ lớn của vectơ kết quả PR có thể được tìm thấy bằng cách sử dụng các phương trình sau:

| PR | = √ (4) ^ 2 + (1) ^ 2

| PR | = √ 17

| PR | = 4.123 đơn vị (Khoảng)

Góc của vectơ kết quả PR có thể được tìm thấy như sau:

Φ = tan ^-1 (1/4)

Φ = 14,04 độ

Câu hỏi thực hành

1. Cho hai vectơ, V = (2, 5) và C = (3, -2), xác định tổng của chúng bằng cách sử dụng quy tắc đầu-đuôi. Ngoài ra, xác định độ lớn và góc của vector kết quả, R .
2. Cho hai vectơ G = (5, 5) và H = (4, -10), hãy xác định tổng của chúng bằng cách sử dụng quy tắc đầu-yo-tail. Ngoài ra, xác định độ lớn và góc của vector kết quả, P .
3. Cho vectơ OA, trong đó O = (-1, 3) và A = (5,2), và vectơ UV, trong đó U = (1, -2) và V = (-2,2), xác định kết quả tổng vectơ S. Sau đó, tìm độ lớn và góc của nó.
4. Cho tứ giác ABCD, xác định giá trị sau:

• DC+ CA =?
• BD+ DC =?
• AD+ DC =?

1. M = 10 m Đông và N = 15 m Bắc. Xác định tổng của hai vectơ, sau đó tìm độ lớn và góc của vectơ kết quả.

Câu trả lời

1. Vectơ kết quả R là R = (5, 3), độ lớn của R là | R | = 5,830 đơn vị, và góc là Φ = 30,96 độ.
2. Vectơ kết quả P là P = (9, 5), độ lớn của P là | P | = 10. 30 đơn vị, và góc là Φ = 29,05 độ.
3. Các vectơ là OA = (6, -1) và UV = (-3, 4), vectơ tổng kết quả S được cho là S = (3, 3), độ lớn của S là | S | = 4,242 đơn vị và góc là Φ = 45 độ.
4. Trong tứ giác đã cho, tổng được tính là:

   DC + CA = DA

   BD + DC = BC

  AD + DC = AC

1. Kết quả của hai vectơ là:

R = M + N

| R | = 18,027 m,

Và góc có thể được tính là:

Φ = tan ^-1 (15/10)

Φ = 56,30 độ.

Do đó, vectơ kết quả là R = 18,027 m , Φ = 56,30 độ Đông Bắc.

Xem thêm:

Hình học Vectơ – Giải thích & Ví dụ dễ hiểu nhất

Hướng của một vectơ là gì? Những ví dụ dễ nhất cho người mới