Công thức của góc giữa 2 đường thẳng trong không gian
30 Tháng Chín, 2021Hôm nay, tintuctuyensinh sẽ hướng dẫn các em cách xác định Công thức của góc giữa 2 đường thẳng...
Contents
Trong hình học vectơ, một trong những khái niệm quan trọng nhất trong việc giải các bài toán trong thế giới thực là sử dụng phương trình vectơ. Phương trình vectơ được định nghĩa là:
“Phương trình vectơ là một phương trình của vectơ mà khi giải ra sẽ cho kết quả dưới dạng một vectơ.”
Trong chủ đề này, chúng ta sẽ thảo luận ngắn gọn về các khái niệm được đề cập sau đây:
Phương trình vectơ là một phương trình liên quan đến n số vectơ. Chính thức hơn, nó có thể được định nghĩa là một phương trình liên quan đến sự kết hợp tuyến tính của các vectơ với các hệ số có thể chưa biết, và khi giải, nó sẽ trả về một vectơ.
Nói chung, một phương trình vectơ được định nghĩa là “Bất kỳ hàm nào nhận bất kỳ ai hoặc nhiều biến hơn và đổi lại là một vectơ.”
Bất kỳ phương trình vectơ nào liên quan đến các vectơ với n số tọa độ tương tự như hệ phương trình tuyến tính với n số tọa độ liên quan đến các số. Ví dụ,
Hãy xem xét một phương trình vectơ,
r <4,5,6> + t <3,4,1> = <8,5,9>
Nó cũng có thể được viết là
<4r, 5r, 6r> + <3t, 4t, 1t> = <8,5,9>
Hoặc là
<4r + 3t, 5r + 4t, 6r + 1t> = <8,5,9>
Để hai vectơ bằng nhau thì tất cả các tọa độ phải bằng nhau, vì vậy nó cũng có thể được viết dưới dạng một hệ phương trình tuyến tính. Cách trình bày như sau:
4r + 3t = 8
5r + 4t = 5
6r + 1t = 9
Vì vậy, phương trình vectơ có thể được giải bằng cách chuyển nó thành một hệ phương trình tuyến tính. Do đó, nó đơn giản hóa và trở nên dễ giải quyết hơn.
Trong cuộc sống hàng ngày của chúng ta, vector đóng một vai trò quan trọng. Hầu hết các đại lượng vật lý được sử dụng là đại lượng vectơ. Vectơ có nhiều ứng dụng thực sự, bao gồm các tình huống được chỉ định bởi lực và vận tốc. Ví dụ, nếu một chiếc ô tô đang chuyển động trên một con đường, nhiều lực khác nhau sẽ tác động lên nó. Một số lực tác dụng theo hướng tiến và một số tác dụng theo hướng lùi để hệ cân bằng. Vì vậy, tất cả các lực này đều là đại lượng vectơ. Chúng tôi sử dụng phương trình vectơ để tìm ra các đại lượng vật lý khác nhau trong 2-D hoặc 3-D, chẳng hạn như vận tốc, gia tốc, động lượng, v.v.
Phương trình vectơ cung cấp cho chúng ta một cách nhìn đa dạng và hình học hơn để xem và giải hệ phương trình tuyến tính.
Nhìn chung, chúng ta có thể kết luận rằng phương trình vectơ là:
x 1. t 1 + x 2 .t 2 + ··· + x k .t k = b
trong đó t 1 , t 2 ,…, t k , b là các vectơ trong Rn và x 1 , x 2 ,…, x k là các vô hướng chưa biết, có cùng tập nghiệm là hệ tuyến tính với ma trận tăng cường của phương trình đã cho .
Do đó, phương trình vectơ đã cho là,
r = r 0 + k v
Hãy hiểu khái niệm này với sự trợ giúp của các ví dụ.
ví dụ 1
Một ô tô chuyển động với vận tốc không đổi trên một đoạn đường thẳng ban đầu tại thời điểm t = 2 vectơ vị trí của ô tô là (1,3,5) thì sau một thời gian tại t = 4, vectơ vị trí của ô tô là (5, 6,8). Viết phương trình vectơ chỉ vị trí của vật. Ngoài ra, hãy biểu diễn nó dưới dạng phương trình tham số.
Giải pháp
Vì phương trình vectơ của một đường thẳng được cho là
r = r 0 + t v
Từ,
r 0 = <1,3,5>
r = <5,6,8>
<5,6,8> = <1,3,5> + 4 v
<5,6,8> – <1,3,5> = 4 v
<4,3,3> = 4 v
v = <1,3 / 4,3 / 4>
Bây giờ, tìm phương trình vectơ về vị trí của đối tượng
r = r 0 + t v
r = <1,3,5> + t <1,3 / 4,3 / 4>
trong đó vectơ r là <x, y, z>
<x, y, z> = <1,3,5> + <1t, 3 / 4t, 3 / 4t>
Biểu diễn dưới dạng phương trình tham số:
Vì hai vectơ chỉ tương đương nếu tọa độ của chúng bằng nhau. Vì vậy, do sự bình đẳng, chúng ta có thể viết là,
x = 1 + t
y = 3 + 3 / 4t
z = 5 + 3 / 4t
Phương trình vectơ của các đường xác định vectơ vị trí của đoạn thẳng liên quan đến vectơ gốc và vectơ hướng và chúng ta có thể tìm ra kích thước của các vectơ tương ứng với độ dài bất kỳ. Điều này làm việc cho các đường thẳng và đường cong.
Lưu ý: Vectơ vị trí được sử dụng để mô tả vị trí của vectơ. Nó là một đường thẳng có một đầu cố định và đầu kia gắn với vectơ chuyển động để xác định vị trí của nó.
Hãy hiểu khái niệm này với sự trợ giúp của các ví dụ.
Ví dụ 2
Viết các phương trình sau dưới dạng phương trình vectơ
Giải pháp
Hãy xem xét phương trình 1 trước:
x = -2y + 7
Vì phương trình đã cho ở trên là phương trình của một đường thẳng:
y = mx + c
Đầu tiên, chúng ta sẽ chọn hai điểm trên đường thẳng cho trước.
Hãy đơn giản hóa phương trình,
x = -2y + 7
cho y = 0
x = 7
Vì vậy, điểm đầu tiên là s (7,0) hoặc OS (7,0)
Bây giờ chúng ta hãy tìm hiểu điểm thứ hai nằm giữa nửa điểm đầu tiên,
Cho x = 14
14 = -2y + 7
-2y = 7
y = -3,5
Vì vậy, điểm thứ hai T (14, -3,5) hoặc OT (14, -3,5)
Sau đó,
HĐH – OT = (7,0) – (14, -3,5)
Hệ điều hành – OT = (-7, 3,5)
Vì vậy, dạng phương trình vectơ của phương trình trên là,
R = <7,0> + k <-7,3,5>
R = <7-7k, 3,5k>
Bây giờ, hãy giải phương trình 2:
3x = -8y + 6
Vì phương trình đã cho ở trên là phương trình của một đường thẳng
y = mx + c
Đầu tiên, chúng ta sẽ chọn hai điểm trên đường thẳng cho trước.
Hãy đơn giản hóa phương trình,
3x = -8y + 6
cho y = 0
x = 2
Vì vậy, điểm đầu tiên là s (2,0) hoặc OS (2,0)
Bây giờ chúng ta hãy tìm hiểu điểm thứ hai nằm giữa nửa điểm đầu tiên,
Cho x = 4
12 = -2y + 7
-2y = 12-7
y = -5/2
Vì vậy, điểm thứ hai T (4, -5/2) hoặc OT (4, -5/2)
Sau đó,
HĐH – OT = (2,0) – (4, -5/2)
HĐH – OT = (-2, 5/2)
Vì vậy, dạng phương trình vectơ của phương trình trên là,
R = <2,0> + k <-2,5 / 2>
R = <2-2k, 5 / 2k>
Bây giờ, chúng ta hãy làm phương trình 3:
x = -3 / 5-8
Vì phương trình đã cho ở trên là phương trình của một đường thẳng
y = mx + c
Đầu tiên, chúng ta sẽ chọn hai điểm trên đường thẳng cho trước.
Hãy đơn giản hóa phương trình,
x = -3 / 5y + 8
cho y = 0
x = 8
Vì vậy, điểm đầu tiên là s (8,0) hoặc OS (8,0)
Bây giờ chúng ta hãy tìm hiểu điểm thứ hai nằm giữa nửa điểm đầu tiên,
Cho x = 16
16 = -3 / 5y + 8
-3 / 5y = 16-8
y = -13,33
Vì vậy, điểm thứ hai T (16, -13,33) hoặc OT (16, -13,33)
Sau đó,
OS – OT = (8,0) – (16, -13,33)
Hệ điều hành – OT = (-8, 13,33)
Vì vậy, dạng phương trình vectơ của phương trình trên là,
R = <8,0> + k <-8,13.33>
R = <8-8k, 13,33k>
Tất cả chúng ta đều quen thuộc với phương trình của đường thẳng y = mx + c, thường được gọi là dạng giao thoa hệ số góc trong đó m là hệ số góc của đường thẳng và x và y là tọa độ điểm hoặc giao điểm được xác định trên trục x và y. . Tuy nhiên, dạng phương trình này không đủ để giải thích hoàn toàn các đặc điểm hình học của đường. Đó là lý do tại sao chúng ta sử dụng một phương trình vectơ để mô tả vị trí và hướng của đường thẳng.
Để tìm các điểm trên đoạn thẳng, chúng ta sẽ sử dụng phương pháp cộng véc tơ. Chúng ta cần tìm ra vectơ vị trí và vectơ chỉ hướng. Đối với vectơ vị trí, chúng ta sẽ thêm vectơ vị trí của điểm đã biết trên đoạn thẳng với vectơ v nằm trên đoạn thẳng, như thể hiện trong hình bên dưới.
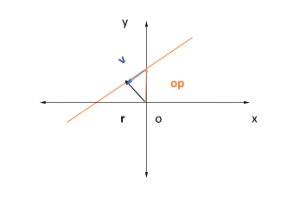

Vì vậy, vectơ vị trí r đối với bất kỳ điểm nào được cho là r = op + v
Khi đó, phương trình vectơ được cho là
R = op + k v
Trong đó k là đại lượng vô hướng thuộc R N , op là vectơ vị trí đối với gốc tọa độ O và v là vectơ chỉ phương. Về cơ bản, k cho bạn biết bạn sẽ đi quãng đường từ p đến q theo hướng xác định bao nhiêu lần. Nó có thể là ½ nếu một nửa khoảng cách sẽ được bao phủ, v.v.
Nếu biết hai điểm trên đường thẳng, chúng ta có thể tìm ra phương trình vectơ của đường thẳng. Tương tự, nếu biết vectơ vị trí của hai điểm op và oq trên một đoạn thẳng, chúng ta cũng có thể xác định phương trình vectơ của đoạn thẳng bằng cách sử dụng phương pháp trừ vectơ.
Ở đâu,
v = op – oq
Do đó, phương trình của vectơ được cho là,
R = op + k v
Hãy giải một số ví dụ để hiểu khái niệm này.
Ví dụ 3
Viết phương trình vectơ của đường thẳng đi qua điểm P (2,4,3) và Q (5, -2,6).
Giải pháp
Gọi vectơ vị trí của các điểm P và Q đối với gốc tọa độ đã cho lần lượt là OP và OQ .
OP = (2,4,3) – (0,0,0)
OP = (2,4,3)
OQ = (5, -2,6) – (0,0,0)
OQ = (5, -2, 6)
Vì chúng ta biết rằng phương trình vectơ của một đường thẳng được xác định là,
R = OP + k v
Trong đó v = OQ – OP
v = (5, -2,6) – (2,4,3)
v = (3, -6, 3)
Vì vậy, phương trình vectơ của đường thẳng được cho là,
R = <2,4,3> + k <3, -6,3>
Ví dụ 4
Xác định phương trình vectơ của đoạn thẳng tại đó k = 0,75. Nếu các điểm đã cho trên đường thẳng được xác định là A (1,7) và B (8,6).
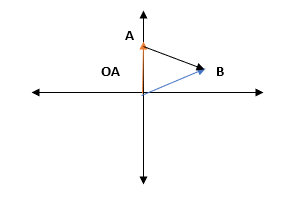

Giải pháp:
k là thang đo có thể thay đổi từ -∞ đến + ∞. Trong trường hợp này, k được cho là 0,75, là khoảng cách được phủ trên AB theo hướng đã cho.
Gọi vectơ vị trí của các điểm A và B đã cho đối với gốc tọa độ lần lượt là OA và OB .
OA = (1,7) – (0,0)
OA = (1,7)
OB = (8,6) – (0,0)
OB = (8,6)
Vì chúng ta biết rằng phương trình vectơ của một đường thẳng được xác định là,
R = OA + k v
Trong đó v = OB – OA
v = (8,6) – (1,7)
v = (7, -1)
Vì vậy, phương trình vectơ của đường thẳng được cho là,
Trong đó k = 0,75
R = <1,7> + 0,75 <7, -1>
Ví dụ 5
Viết phương trình véc tơ của đường thẳng đi qua điểm P (-8,5) và Q (9,3).
Giải pháp
Gọi vectơ vị trí của các điểm P và Q đối với gốc tọa độ đã cho lần lượt là OP và OQ .
OP = (-8,5) – (0,0)
OP = (-8,5)
OQ = (9,3) – (0,0)
OQ = (9,3)
Vì chúng ta biết rằng phương trình vectơ của một đường thẳng được xác định là,
R = OP + k v
Trong đó v = OQ – OP
v = (9,3) – (-8,5)
v = (17, -2)
Vì vậy, phương trình vectơ của đường thẳng được cho là,
R = <-8,5> + k <17, -2>
Trước đó, chúng ta đã thảo luận về phương trình vectơ của một đường thẳng. Bây giờ chúng ta sẽ thảo luận về phương trình vectơ của một đường tròn có bán kính r và với một số tâm c, mà chúng ta thường nói rằng đường tròn có tâm tại c (0,0), nhưng nó có thể nằm ở bất kỳ điểm nào khác trong mặt phẳng.
Phương trình vectơ của một đường tròn được cho là
r (t) = <x (t), y (t)>
trong đó x (t) = r.cos (t) và y (t) = r.sin (t), r là bán kính của đường tròn và t là góc được xác định.
Chúng ta hãy xem xét một đường tròn có tâm c và bán kính r, như trong hình bên dưới.
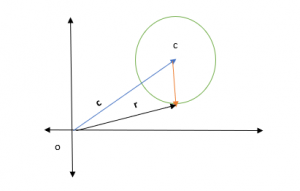

Vectơ vị trí của bán kính và tâm c lần lượt là r và c . Khi đó bán kính của hình tròn được biểu diễn bằng vectơ CR, trong đó CR được cho là r – c.
Vì bán kính được cho là r nên độ lớn nếu CR có thể được viết dưới dạng
| CR | = r ^ 2
Hoặc là
( r – c ). ( r – c ) = r ^ 2
Hoặc là
| r – c | = r
Đây cũng có thể được gọi là một phương trình vectơ của một đường tròn.
Ví dụ 5
Viết phương trình vectơ và phương trình macte của đường tròn có tâm c tại (5,7) và bán kính 5m.
Giải pháp
Phương trình vectơ của một đường tròn:
| r – c | = r
| r – <5,7> | = 5
( r – <5,7>) ^ 2 = 25
Phương trình Descartes của một đường tròn:
(xh) ^ 2 + (yk) ^ 2 = r 2
(x-5) ^ 2 + (y-7) ^ 2 = 25
Ví dụ 6
Xác định xem điểm (2,5) có nằm trên đường tròn hay không với phương trình vectơ của đường tròn đã cho là | r – <- 6,2> | = 3.
Giải pháp
Chúng ta phải tìm xem liệu điểm đã cho có nằm bên trong đường tròn hay không đã cung cấp phương trình vectơ của đường tròn.
Vì đặt giá trị của điểm vào phương trình véc tơ đã cho
= | <2,5> – <- 6,2> |
= | <2 + 6,5-2> |
= | <8,3> |
= √ ((8) ^ 2 + (3) ^ 2 )
= √ (64 + 9)
= √ (73) ≠ 3
Do đó, điểm không nằm bên trong vòng tròn.
Xem thêm:
Phép nhân theo phương pháp vô hướng-Phép toán và các ví dụ
Hướng dẫn thực hiện phép trừ vectơ chi tiết nhất
Q = <-2,6> P = <3, -1>
Q = <1,8> P = <9, -3>
Câu trả lời