Sắp xếp thứ tự các phân số chuẩn không cần chỉnh

Làm thế nào để sắp xếp các phân số?

Thứ tự phân số đơn giản có nghĩa là sắp xếp phân số từ nhỏ nhất đến lớn nhất (thứ tự tăng dần) hoặc lớn nhất đến nhỏ nhất (thứ tự giảm dần).

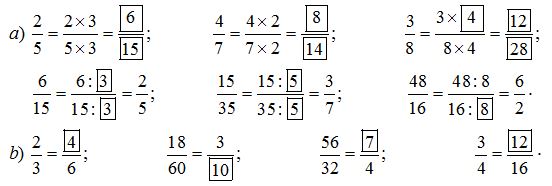
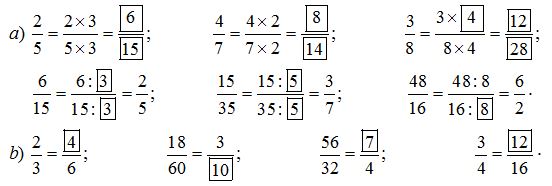
Có hai phương pháp phổ biến hoặc sắp xếp phân số.

Đó là:

• Sử dụng một mẫu số chung.
• Thay đổi phân số thành số thập phân và sau đó sắp xếp thứ tự.

Sắp xếp thứ tự các phân số bằng mẫu số chung

Các phân số có thể được so sánh và sắp thứ tự bằng cách xác định các phân số tương đương của chúng với mẫu số chung. Mẫu số chung được tạo ra bằng cách sử dụng bội chung của hai số, ví dụ 24 là bội chung nhỏ nhất của 8 và 12.

8 x 3 = 24

12 x 2 = 24

Tuy nhiên, 8 và 12 có một số bội số chung khác, tuy nhiên, 24 là bội số thấp nhất.

Thay đổi phân số thành số thập phân và sau đó sắp xếp thứ tự

Chuyển đổi phân số thành số thập phân là một phương pháp khác để sắp xếp thứ tự phân số.

ví dụ 1

Sắp xếp các phân số sau theo thứ tự tăng dần.

3/4, 1/2, 4/5, 3/8

Giải pháp

Đầu tiên chuyển đổi tất cả các phân số thành số thập phân như hình dưới đây:

3/4 = 0,75

1/2 = 0,5

4/5 = 0,8

3/8 = 0,375

Vì tất cả các phân số đều có chữ số hàng đơn vị là 0 nên hãy so sánh chúng bằng cách kiểm tra chữ số hàng phần mười.

Bây giờ hãy sắp xếp các số thập phân theo thứ tự giảm dần

0,8, 0,75, 0,5, 0,375,

Có câu trả lời cuối cùng là 4/5, 3/4, 1/2 và 3/8

Ngoài ra còn có các phương pháp sắp xếp thứ tự các phân số khác như tính tỷ lệ phần trăm của chúng.

Ví dụ , vấn đề có thể được giải quyết bằng cách biểu thị dưới dạng phần trăm.

Đặt hàng 1/10, 1/5, 1/4, 1/2, 1/3

Sắp xếp thứ tự các phân số từ Ít nhất đến Lớn nhất 

Hãy hiểu điều này với sự trợ giúp của các ví dụ.

Ví dụ 2

Sắp xếp các phân số sau theo thứ tự tăng dần:

1/2, 2/3, 7/12, 5/6, 1/4

Giải pháp

• Đầu tiên hãy xác định tất cả các mẫu số của các phân số. Và trong trường hợp này, các mẫu số là 2, 3, 12, 6 và 4.
• Tính bội chung nhỏ nhất của tất cả các mẫu số. Bạn nhìn vào LCM của hai số cùng một lúc và kiểm tra xem các mẫu số khác có phải là thừa số của LCM được tính hay không
• Bội số chung nhỏ nhất của các mẫu số 2, 3, 12, 6 và 4 là 12
• Bước tiếp theo là viết lại mỗi phân số dưới dạng phân số tương đương với mẫu số 12.

1/2 x 6/6 = 6/12

2/3 x 4/4 = 8/12

7/12 x 1/1 = 7/12

5/6 x 2/2 = 10/12

1/4 x 3/3 = 3/12

Giờ đây, tất cả các phân số đều có chung một mẫu số, do đó, việc đặt các phân số theo thứ tự tăng dần bằng cách so sánh các tử số của chúng sẽ dễ dàng hơn.

Bằng cách so sánh các tử số, câu trả lời cuối cùng trở thành: 1/4, 1/2, 7/12, 2/3, 5/6.

Các ví dụ khác

1. Sắp xếp các thứ sau theo thứ tự tăng dần:

1/2, 1/4, 3/4

Giải pháp

Tìm LCM của 2, 4 là 4

Nhân 1/2 = 1/2 × 2/2 = 2/4

Vì tử số 4 còn lại trong tất cả các phân số, nên thứ tự phân số như sau:

1/4 <1/2 <3/4

2. Sắp xếp các phân số dưới đây theo thứ tự tăng dần:

3/5, 3/7, 25/9

Giải pháp

Xác định LCM của 5, 7 và 25 là 175

Nhân mỗi phân số với LCM như sau:

3/5 = 3/5 × 35/35 = 105/175

3/7 = 3/7 × 25/25 = 75/175

9/25 = 9/25 × 7/7 = 63/175

Bây giờ sắp xếp các phân số theo thứ tự tăng dần như sau:

25/9, 3/7, 3/5

3. Thứ tự phân số từ bé nhất đến lớn nhất.

2/5, 4/7, 5/6

Giải pháp

Tìm LCM của 5, 7 và 6 = 210

2/5 = 2/5 × / 42/42 = 84/210

4/7 = 4/7 × 30/30 = 120/210

5/6 = 5/6 × 35/35 = 175/210

Bây giờ các phân số theo thứ tự tăng dần = 2/5 <4/7 <5/6

4. Sắp xếp các phân số sau theo thứ tự tăng dần

1/3, 6/9, 9/18

Giải pháp

Xác định LCM của các mẫu số là 18.

1/3 = 1/3 × 6/6 = 6/18

6/9 = 6/9 × 2/2 = 12/18

Hiện nay,

6/18 <9/18 <12/18 và do đó phân số theo thứ tự tăng dần;

1/3 <9/18 <6/9

5. Thứ tự các phân số dưới đây từ nhỏ nhất đến lớn nhất.

3/9, 25/9, 5/20

Giải pháp

Bắt đầu bằng cách tính LCM của các mẫu số 4, 20 và 25 = 100

3/4 = 3/4 × 25/25 = 75/100

9/25 = 9/25 × 4/4 = 36/100

5/20 = 5/20 × 5/5 = 25/100

Như vậy;

25/100 <36/100 <75/100

Do đó, phân số từ thấp nhất đến lớn nhất là

5/20 <9/25 <3/4

6. Sắp xếp các phân số này theo thứ tự tăng dần:

2/15, 3/18, 9/10

Giải pháp

Tính LCM của các mẫu số 15, 18 và 10 là 90

2/15 = 2/15 × 6/6 = 12/90

3/18 = 3/15 × 5/5 = 15/90

9/10 = 9/10 × 9/9 = 81/90

Và do đó, các phân số theo thứ tự tăng dần là: 2/15 <3/18 <9/10

7. Liệt kê các phân số sau theo thứ tự tăng dần

16/15, 15 / 14,14 / 12

Giải pháp

Tính LCM của 15, 14 và 12 là 420

16/15 = 16/15 × 28/28 = 448/420

15/14 = 15/14 × 30/30 = 450/420

14/12 = 14/12 × 35/35 = 490/420

Vì vậy,

448/420 <450/420 <4 90/4200420 Và do đó các phân số theo thứ tự tăng dần:

16/15 <15/14 <14/12

8. Sắp xếp các phân số này theo thứ tự tăng dần:

2/3, 3/4, 4/5

Giải pháp

Bắt đầu bằng cách tính LCM của các mẫu số 3, 4 và 5 là 60

2/3 = 2/3 × 20/20 = 40/60

3/4 = 3/4 × 15/15 = 45/60

4/5 = 4/5 × 12/12 = 48/60

Bây giờ sắp xếp các phân số như sau:

40/60 <45/60 <48/60 Và do đó, các phân số từ nhỏ nhất đến lớn nhất là:

2/3 <3/4 <4/5

Xem thêm:

Phân số – Định nghĩa & loại phân số thường gặp nhất

Hướng dẫn cách rút gọn phân số nhanh nhất

Câu hỏi thực hành

1. Giáo viên đang chia một túi bóng tennis cho học sinh của mình. Anh ta đưa 2/9 quả bóng cho Mary, 1/3 quả bóng cho Harish, 7/27 quả bóng cho James, và anh ta giữ 5/27 cho mình. Xếp thứ tự phần chia của họ từ lớn nhất đến nhỏ nhất.
2. Tuần trước, Pedro đã nghe 2/3 bản nhạc yêu thích của mình trong khi Adam và Philip lần lượt nghe 3/5 và 4/7 bản nhạc yêu thích của họ. Sắp xếp các phân số này theo thứ tự giảm dần.
3. Sala đã tham gia 4 hoạt động thể thao khác nhau. Anh ấy dành 9/10 giờ để bơi, 2/3 giờ chơi bóng đá, 1/3 và 2/4 giờ chạy bộ và nhảy tương ứng. Sắp xếp thời gian anh ấy tham gia các hoạt động thể thao khác nhau từ lớn nhất đến nhỏ nhất.