Tứ phân vị là gì? Xem xong 5 phút hiểu luôn.
Contents
Số hợp lý là gì?
Một số hữu tỉ, trong Toán học, có thể được định nghĩa là bất kỳ số nào có thể được biểu diễn dưới dạng p / q trong đó q ≠ 0. Ngoài ra, chúng ta có thể nói rằng bất kỳ phân số nào đều phù hợp với loại số hữu tỉ, trong đó mẫu số và tử số là các số nguyên và mẫu số không bằng không. Khi chia số hữu tỉ (tức là phân số), kết quả sẽ ở dạng thập phân, có thể là số thập phân kết thúc hoặc số thập phân lặp lại.
Làm thế nào để nhận biết một số hữu tỉ?
Để xác định xem một số là số hữu tỉ hay không, hãy kiểm tra các điều kiện dưới đây.
- Nó được biểu diễn dưới dạng p / q, trong đó q ≠ 0 .
- Tỷ lệ p / q có thể được đơn giản hóa hơn nữa và được biểu diễn ở dạng thập phân.
Tập hợp các số hữu tỉ:
- Bao gồm số dương, số âm và số 0
- Có thể được biểu thị dưới dạng phân số
Ví dụ về Số hợp lý:
| p | q | p / q | Hợp lý |
| 10 | 2 | 10/2 = 5 | Hợp lý |
| 1 | 1000 | 1/1000 = 0,001 | Hợp lý |
| 50 | 10 | 50/10 = 5 | Hợp lý |
Các loại số hợp lý
Một số là hữu tỉ nếu chúng ta có thể viết nó dưới dạng phân số, trong đó cả mẫu số và tử số đều là số nguyên và mẫu số là một số khác không.
Sơ đồ dưới đây giúp chúng ta hiểu thêm về các bộ số.
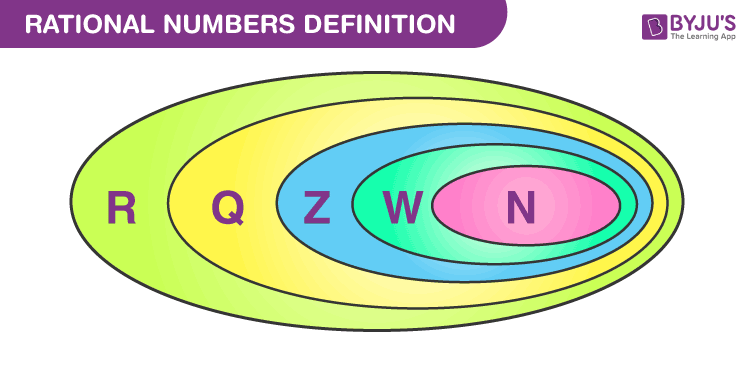

- Số thực (R) bao gồm tất cả các số hữu tỉ (Q).
- Số thực bao gồm các số nguyên (Z).
- Số nguyên liên quan đến số tự nhiên (N).
- Mọi số nguyên đều là số hữu tỉ vì mọi số nguyên đều có thể được biểu diễn dưới dạng phân số.
Dạng chuẩn của số hợp lý
Dạng chuẩn của một số hữu tỉ có thể được xác định nếu nó không có thừa số chung nào ngoại trừ một thừa số giữa số bị chia và số bị chia và do đó số chia là dương.
Ví dụ, 12/36 là một số hữu tỉ. Nhưng nó có thể được đơn giản hóa là 1/3; thừa số chung giữa số bị chia và số bị chia chỉ là một. Vì vậy, chúng ta có thể nói rằng số hữu tỉ ⅓ ở dạng chuẩn.
Số hợp lý dương và số hợp lý phủ định
Như chúng ta biết rằng số hữu tỉ có dạng p / q, trong đó p và q là các số nguyên. Ngoài ra, q phải là một số nguyên khác không. Số hữu tỉ có thể là số dương hoặc số âm. Nếu số hữu tỉ dương thì cả p và q đều là số nguyên dương. Nếu số hữu tỉ có dạng – (p / q) thì p hoặc q nhận giá trị âm. Nó có nghĩa là
– (p / q) = (-p) / q = p / (- q).
Bây giờ, chúng ta hãy thảo luận một số ví dụ về số hữu tỉ âm và dương.
| Số hợp lý dương | Số hợp lý phủ định |
|---|---|
| Nếu cả tử số và mẫu số cùng dấu. | Nếu tử số và mẫu số trái dấu. |
| Tất cả đều lớn hơn 0 | Tất cả đều nhỏ hơn 0 |
| Ví dụ về số hữu tỉ dương: 17/12, 11/9 và 3/5 | Ví dụ về số hữu tỉ âm: -2/17, 9 / -11 và -1/5. |
Các phép toán số học trên các số hợp lý
Trong Toán học, các phép toán số học là các phép toán cơ bản mà chúng ta thực hiện trên các số nguyên. Chúng ta hãy thảo luận ở đây làm thế nào chúng ta có thể thực hiện các phép toán này trên các số hữu tỉ, chẳng hạn như p / q và s / t.
Bổ sung: Khi cộng p / q và s / t, chúng ta cần làm cho mẫu số giống nhau. Do đó, chúng ta nhận được (pt + qs) / qt.
Ví dụ: 1/2 + 3/4 = (2 + 3) / 4 = 5/4
Phép trừ: Tương tự, nếu chúng ta trừ p / q và s / t, thì chúng ta cũng phải làm cho mẫu số giống nhau, trước tiên, sau đó thực hiện phép trừ.
Ví dụ: 1/2 – 3/4 = (2-3) / 4 = -1/4
Phép nhân: Trong trường hợp nhân, trong khi nhân hai số hữu tỉ thì tử số và mẫu số của số hữu tỉ được nhân tương ứng. Nếu p / q nhân với s / t thì ta được (p × s) / (q × t).
Ví dụ: 1/2 × 3/4 = (1 × 3) / (2 × 4) = 3/8
Phép chia: Nếu p / q chia cho s / t, thì nó được biểu diễn dưới dạng:
(p / q) ÷ (s / t) = pt / qs
Ví dụ: 1/2 ÷ 3/4 = (1 × 4) / (2 × 3) = 4/6 = 2/3
Nghịch đảo nhân của số hữu tỉ
Khi số hữu tỉ được biểu diễn dưới dạng p / q, là một phân số, thì nghịch đảo nhân của số hữu tỉ là nghịch đảo của phân số đã cho.
Ví dụ: 4/7 là một số hữu tỉ, thì phép nhân nghịch đảo của số hữu tỉ 4/7 là 7/4, sao cho (4/7) x (7/4) = 1
Thuộc tính số hợp lý
Vì số hữu tỉ là tập con của số thực nên số hữu tỉ sẽ tuân theo tất cả các tính chất của hệ số thực. Một số tính chất quan trọng của số hữu tỉ như sau:
- Kết quả luôn là một số hữu tỉ nếu chúng ta nhân, cộng hoặc trừ hai số hữu tỉ bất kỳ.
- Một số hữu tỉ không đổi nếu chúng ta chia hoặc nhân cả tử số và mẫu số với cùng một thừa số.
- Nếu chúng ta thêm số 0 vào một số hữu tỉ thì chúng ta sẽ nhận được chính số đó.
- Số hữu tỉ được đóng dưới phép cộng, trừ và nhân.
Số hợp lý và Số vô tỷ
Có một sự khác biệt giữa Số hợp lý và Số không hợp lý . Một phân số có mẫu số khác không được gọi là một số hữu tỉ. Số ½ là số hữu tỉ vì nó được đọc là số nguyên 1 chia cho số nguyên 2. Tất cả các số không hữu tỉ được gọi là số vô tỉ. Kiểm tra biểu đồ dưới đây, để phân biệt giữa hợp lý và không hợp lý.
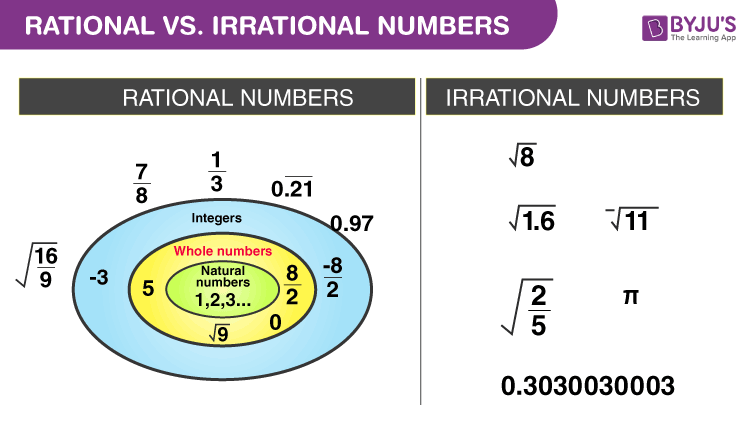

Số hợp lý có thể là số dương, số âm hoặc số không. Trong khi xác định một số hữu tỉ âm, dấu âm ở phía trước hoặc cùng với tử số của số, đó là ký hiệu toán học tiêu chuẩn. Ví dụ, chúng tôi biểu thị âm của 5/2 là -5/2.
Một số vô tỉ không thể được viết dưới dạng một phân số đơn giản nhưng có thể được biểu diễn bằng một số thập phân. Nó có vô số chữ số không lặp lại sau dấu thập phân. Một số số vô tỉ thường gặp là:
Pi (π) = 3,142857…
Số Euler (e) = 2.7182818284590452 …….
√2 = 1,414213…
Làm thế nào để tìm các số hữu tỉ giữa hai số hữu tỉ?
Có “n” số hữu tỉ giữa hai số hữu tỉ. Có thể dễ dàng tìm được số hữu tỉ giữa hai số hữu tỉ bằng hai phương pháp khác nhau. Bây giờ, chúng ta hãy xem xét hai phương pháp khác nhau.
Phương pháp 1:
Tìm phân số tương đương của các số hữu tỉ đã cho và tìm các số hữu tỉ ở giữa chúng. Những số đó phải là số hữu tỉ bắt buộc.
Phương pháp 2:
Tìm giá trị trung bình của hai số hữu tỉ đã cho. Giá trị trung bình phải là số hữu tỉ bắt buộc. Để tìm được nhiều số hữu tỉ hơn, hãy lặp lại quy trình tương tự với số hữu tỉ cũ và số hữu tỉ mới thu được.
Các ví dụ đã giải quyết
Ví dụ 1:
Xác định mỗi số sau là vô tỷ hay hữu tỷ: ¾, 90/12007, 12 và √5.
Giải pháp :
Vì một số hữu tỉ là một số có thể được biểu diễn dưới dạng một tỷ số. Điều này chỉ ra rằng nó có thể được biểu thị dưới dạng phân số trong đó cả mẫu số và tử số đều là số nguyên.
- ¾ là một số hữu tỉ vì nó có thể được biểu diễn dưới dạng phân số. 3/4 = 0,75
- Phân số 90/12007 là hữu tỉ.
- 12, cũng được viết là 12/1. Lại là một số hữu tỉ.
- Giá trị của √5 = 2,2360679775 …… .. Đây là giá trị không kết thúc và do đó không thể viết dưới dạng phân số. Nó là một con số vô tỉ.
Ví dụ 2 :
Xác định xem phần hỗn hợp, 1 1 / 2 là một con số hợp lý.
Giải pháp:
Hình thức đơn giản nhất của 1 1 / 2 là 3/2
Numerator = 3, là một số nguyên
Mẫu số = 2, là một số nguyên và không bằng 0.
Vì vậy, đúng, 3/2 là một số hữu tỉ.
Ví dụ 3:
Xác định xem các số đã cho là hữu tỉ hay vô tỉ.
(a) 1,75 (b) 0,01 (c) 0,5 (d) 0,09 (d) √3
Giải pháp:
Các số đã cho có định dạng thập phân. Để tìm xem một số đã cho có phải là số thập phân hay không, chúng ta phải chuyển nó thành dạng phân số (tức là, p / q)
Nếu mẫu số của phân số không bằng 0, thì số đó là số hữu tỉ, hoặc nếu không, nó là số vô tỉ.
| Số thập phân | Phân số | Số hữu tỉ |
| 1,75 | 7/4 | Đúng |
| 0,01 | 1/100 | Đúng |
| 0,5 | 1/2 | Đúng |
| 0,09 | 1/11 | Đúng |
| √ 3 | ? | Không |
Câu hỏi thường gặp về Số hợp lý
Số hữu tỉ là gì? Cho ví dụ.
Số hữu tỉ là số có dạng p / q, trong đó p và q là các số nguyên và q không bằng 0. Một số ví dụ về số hữu tỉ bao gồm 1/3, 2/4, 1/5 , 9/3, v.v.
Sự khác nhau giữa số hữu tỉ và số vô tỉ là gì?
Một số hữu tỉ là một số được biểu thị bằng tỉ số của hai số nguyên, trong đó mẫu số không được bằng 0, ngược lại một số vô tỉ không thể được biểu thị dưới dạng phân số. Số hữu tỉ là số thập phân tận cùng nhưng số vô tỉ là không tận cùng. Ví dụ về số hữu tỉ là 10/2, và đối với một số vô tỉ là giá trị toán học nổi tiếng Pi (π) bằng 3,141592653589 …….
0 có phải là số hữu tỉ không?
Đúng, 0 là một số hữu tỉ vì nó là một số nguyên, có thể được viết dưới bất kỳ dạng nào như 0/1, 0/2, trong đó b là một số nguyên khác không. Nó có thể được viết dưới dạng: p / q = 0/1. Do đó, chúng tôi kết luận rằng 0 là một số hữu tỉ.
7 có phải là số hữu tỉ không?
9 có phải là số hữu tỉ không?
Tìm một số hữu tỉ từ 3 đến 4.
= 7/2