Thuộc tính giao hoán – Những cách giải nhanh gọn nhẹ

Thuộc tính giao hoán – Thuộc tính & Ví dụ

Từ ‘ commutative ‘ được lấy từ từ tiếng Pháp ‘ commute ‘ có nghĩa là di chuyển xung quanh. Đối với các số hoặc biến giữ thuộc tính giao hoán, chúng có thể di chuyển xung quanh (trong một biểu thức) giống như một dấu đi lại và cho kết quả tương tự khi một phép toán cụ thể được áp dụng cho chúng. Các giao hoán đã được biết đến từ thời cổ đại, nhưng các nhà toán học bắt đầu sử dụng nó ở phần cuối của 18 ^thứ thế kỷ.

Thuộc tính giao hoán có liên quan đến các phép toán và hàm nhị phân . Nếu hai phần tử đang theo sau thuộc tính giao hoán trong một số phép toán, thì chúng được cho là được chuyển đổi theo phép toán cụ thể đó.

Thuộc tính giao hoán là gì?

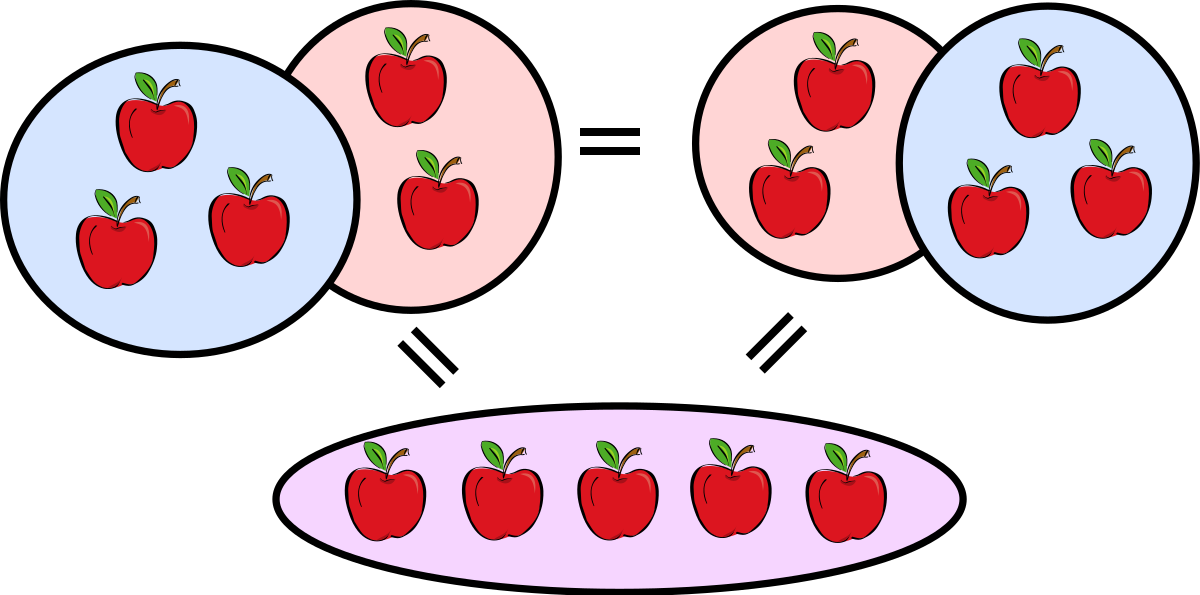
Trong một biểu thức toán học nào đó, nếu việc thay đổi thứ tự các số không làm thay đổi kết quả thì phép toán đó có tính chất giao hoán. Chỉ có phép cộng và phép nhân là giao hoán, trong khi phép trừ và phép chia là không giao hoán.

QUẢNG CÁO

Thuộc tính giao hoán của phép cộng

Theo tính chất giao hoán của phép cộng, nếu các số được thêm vào bất kỳ thứ tự nào thì kết quả là như nhau. Giả sử nếu cộng số a với số b và được kết quả bằng số p nào đó thì nếu ta đổi vị trí của a và b thì kết quả vẫn bằng p tức là

a + b = b + a = p

Các số a và b được gọi là addend.

Thuộc tính này cũng hoạt động cho nhiều hơn hai số, tức là

a + b + c + d = d + c + b + a

ví dụ 1

Chứng tỏ rằng các số sau tuân theo tính chất giao hoán của phép cộng:

2, 4, 6 và 9

2 + 4 + 6 + 9 = 21

9 + 6 + 4 + 2 = 21

Kết quả là như nhau trong cả hai trường hợp. Vì thế,

2 + 4 + 6 + 9 = 9 + 6 + 4 + 2

Ví dụ thực tế là nếu bạn muốn thực hiện một cuộc khảo sát trong xã hội của bạn về số lượng trẻ em trong mỗi ngôi nhà, bạn có thể bắt đầu từ bất kỳ ngôi nhà nào và đếm số trẻ em trong mỗi ngôi nhà và tổng số chúng. Thứ tự của ngôi nhà không quan trọng ở đây.

Các ví dụ thực tế khác là đeo một đôi găng tay, một đôi giày và một đôi tất là những ví dụ về tính chất giao hoán.

Tính chất giao hoán của phép nhân

Theo tính chất giao hoán của phép nhân, nếu các số được nhân theo thứ tự nào thì kết quả là như nhau. Giả sử nếu nhân số a với số b và được kết quả bằng một số q , thì nếu ta đổi vị trí của a và b thì kết quả vẫn bằng q tức là

a × b = b × a = q

Thuộc tính này cũng hoạt động cho nhiều hơn hai số, tức là

a × b × c × d = d × c × b × a

Các phép hợp của hàm và phép nhân ma trận cũng không có tính chất giao hoán.

Ví dụ 2

Chứng tỏ rằng các số sau tuân theo tính chất giao hoán của phép nhân:

2, 4, 6 và 9

2 × 4 × 6 × 9 = 432

9 × 6 × 4 × 2 = 432

Kết quả là như nhau trong cả hai trường hợp. Vì thế,

2 × 4 × 6 × 9 = 9 × 6 × 4 × 2

Tại sao Phép trừ và Phép chia là Không tương đối?

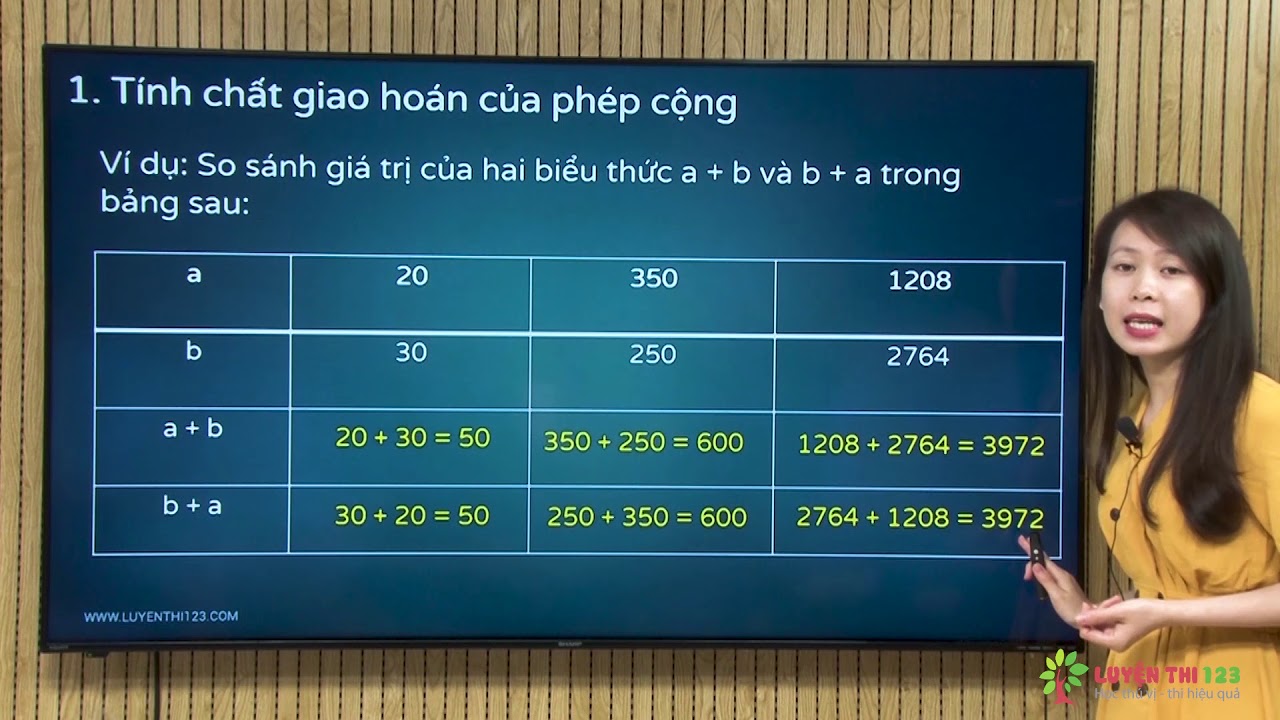
Để hiểu tại sao phép trừ và phép chia không tuân theo quy tắc giao hoán, hãy theo dõi các ví dụ dưới đây.

Ví dụ 3

Cho biết biểu thức sau có đúng không.

a – b = b – a

• Bước 1: Những gì bạn cần thể hiện?

a – b = b – a

• Bước 2: Lấy phía bên trái và cố gắng chứng minh nó bằng với phía bên phải.

a – b

• Bước 3: Lấy -1 chung.

–1 (- a + b) = – (- a + b)

• Bước 4: Đảo ngược các phụ đề.

– (ba)

• Bước 5: Xem bạn có nhận được kết quả mong muốn hay không.

a – b = – (b – a)

• Bước 6: Nêu những phát hiện của bạn.

Từ,

a – b = – (b – a)

Vì thế,

a – b ≠ b – a

Do đó, biểu thức đã cho là sai và không tuân theo tính chất giao hoán.

Xem thêm:

Thừa số nguyên tố và những cách giải nhanh nhất

Thuộc tính danh tính – Giải thích với các ví dụ dễ hiểu nhất

Ví dụ 4

Cho biết biểu thức sau có đúng không.

2a ÷ a = a ÷ 2a

• Bước 1: Những gì bạn cần thể hiện?

2a ÷ a = a ÷ 2a

• Bước 2: Lấy phía bên tay trái.

2a ÷ a

• Bước 3: Giải quyết.

2a ÷ a = 2

• Bước 4: Giải quyết bên tay phải bây giờ.

a ÷ 2a = 1/2

• Bước 5: Nêu những phát hiện của bạn.

Từ,

2a ÷ a = 2

a ÷ 2a = 1/2

Vì thế,

2a ÷ a ≠ a ÷ 2a

Do đó, biểu thức đã cho là sai và không tuân theo tính chất giao hoán.

Vấn đề thực hành

1. Nội dung nào sau đây tuân theo quy luật giao hoán?
2. 9 + 12
3. –7 × 6
4. 72 ÷ 5
5. –99 – 7

Câu trả lời:

1. Có b. Vâng C. Không d. Đúng
2. Bảng dưới đây cho thấy túi tiền của 4 sinh viên.

Nếu tổng số tiền tiêu vặt của học sinh A và B bằng tổng số tiền tiêu vặt của học sinh C và D, hãy tìm giá trị của x .

Trả lời: 7

1. Chứng tỏ rằng 12% của 25 giống với 25% của 12.

1. Có hai khu vực để xe ô tô tại tầng hầm. Ở khu vực A người ta đỗ ô tô sao cho có 6 ô tô đỗ thành 12 hàng, còn ở khu vực B có 12 ô tô đỗ mỗi hàng thành 6 hàng còn lại. Có bao nhiêu ô tô ở bãi đậu xe?

Trả lời: 144

1. Sam mang về nhà 4 thùng chai. Mỗi thùng có 8 hàng chai, mỗi hàng có thể chứa 6 chai. Sam đã mua bao nhiêu chai?

Trả lời: 192

1. Nina đã làm 8 chiếc bánh quy và phân phát cho 4 người bạn của cô ấy. Liza đã làm 4 chiếc bánh quy và phân phát cho 8 người bạn của cô ấy. Việc phân chia cookie này có tuân theo luật giao hoán không?

Trả lời: Không, luật giao hoán không đúng với phép chia tức là 8/4 ≠ 4/8

1. Ali thức dậy vào buổi sáng, dành 10 phút trong phòng vệ sinh, 12 phút trong bữa sáng và 7 phút để thay đồ trước khi đi học. Mặt khác, James dành 7 phút trong phòng vệ sinh, 12 phút ăn sáng và 10 phút chuẩn bị trước khi đến trường.

Tổng thời gian Ali và James dành cho việc chuẩn bị sẵn sàng có bằng nhau không?

Trả lời có