Tứ giác và những kiến thức hiểu biết về nó

Các loại hình dạng khác nhau về cạnh hoặc góc. Có nhiều hình dạng có 4 cạnh, nhưng sự khác biệt về góc độ ở các mặt khiến chúng trở nên độc đáo. Ta gọi các hình có 4 cạnh này là tứ giác.

Trong bài viết này, bạn sẽ học:

• Tứ giác là gì?
• Các dạng khác nhau của tứ giác có dạng như thế nào?
• Ngoài ra, bạn sẽ tìm hiểu về các tính chất của tứ giác.

Tứ giác là gì?

Như từ gợi ý, ‘ Quad ‘ có nghĩa là bốn và ‘ lateral ‘ có nghĩa là cạnh, do đó hình tứ giác là một đa giác hai chiều khép kín được tạo thành từ các đoạn 4 dòng . Nói một cách dễ hiểu, tứ giác là một hình có bốn cạnh .

Hình tứ giác ở khắp mọi nơi! Từ những cuốn sách, giấy tờ biểu đồ, phím máy tính, tivi và màn hình điện thoại di động. Danh sách các ví dụ trong thế giới thực về tứ giác là vô tận.

Các loại tứ giác

Có sáu tứ giác trong hình học . Một số hình tứ giác chắc chắn đã quen thuộc với bạn, trong khi những hình khác có thể không quá quen thuộc.

Chúng ta hãy xem xét.

• Hình chữ nhật
• Hình vuông
• Trapezium
• Hình bình hành
• Hình thoi
• cánh diều

 Một hình chữ nhật

Hình chữ nhật là hình tứ giác có 4 góc vuông (90 °). Trong một hình chữ nhật, các cặp cạnh đối diện đều song song và có độ dài bằng nhau.

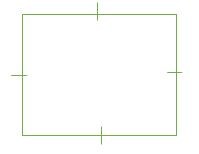
Thuộc tính của hình chữ nhật:

• Tất cả các góc đều là góc vuông
• Các đường chéo là đồng dư.

Hình chữ nhật rất tiện dụng để có xung quanh. Ví dụ như hộp đựng giày, thớt, tờ giấy, khung ảnh,… đều có dạng hình chữ nhật.

Hình chữ nhật dễ xếp chồng lên nhau vì chúng có hai cặp cạnh song song. Các góc vuông của chúng đảm bảo những thứ được xây dựng như nhà ở, cao ốc văn phòng, trường học, v.v … luôn đứng thẳng và cao.

Hình vuông

Hình vuông là tứ giác có 4 góc vuông (90 °). Trong một hình vuông, cả hai cặp cạnh đối diện đều song song và có độ dài bằng nhau.

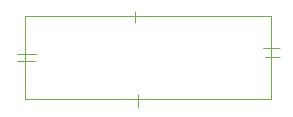
Các thuộc tính của hình vuông:

• Tất cả các cạnh của hình vuông đều đồng dư.
• Tất cả các góc đều là góc vuông theo định nghĩa.

Các ví dụ trong đời thực – thế giới về hình vuông bao gồm: phím máy tính, đế lót ly, khoảng trống trên bàn cờ, v.v.

Hình bình hành

Hình bình hành là tứ giác có 2 cặp cạnh đối song song và bằng nhau. Tương tự, các góc đối diện trong một hình bình hành có số đo bằng nhau.

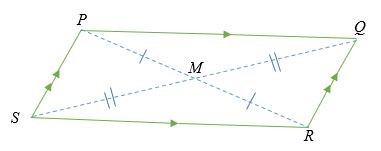
Trong hình bình hành PQRS , cạnh PQ song song với cạnh SR và cạnh PS song song với cạnh QR. Điểm M là trung điểm của hai đường chéo của hình bình hành.

Do đó, độ dài PM = MR và độ dài SM = MQ

Hình thoi

Hình thoi là hình tứ giác có độ dài bốn cạnh bằng nhau. Các cạnh đối của một hình thoi bằng nhau và song song và các góc đối diện bằng nhau.

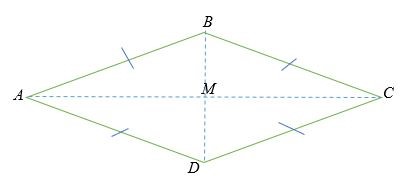
Hình thoi ABCD là hình thoi trong đó AB song song với DC và AD cũng song song với BC.

Hai đường chéo AC = BD và M là giao điểm của hai đường chéo.

Trapezium

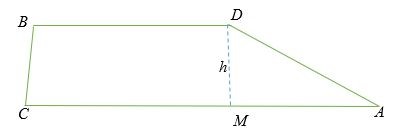
Hình thang hay hình thang đều có một cặp cạnh đối song song. Các cạnh của hình thang được gọi là đáy và đường vuông góc từ bất kỳ đỉnh nào của hình thang đến đáy được gọi là chiều cao.

ABCD là hình thang trong đó cạnh BD song song với cạnh CA. Đường trung trực DM là đường cao ( h ) của hình thang còn BD và CA là các đáy.

cánh diều

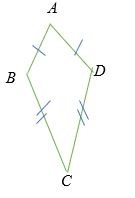
Diều là hình tứ giác có độ dài hai cặp cạnh bằng nhau và các cạnh này kề nhau.

Tính chất của hình thoi

• Tất cả các bên đều đồng dư theo định nghĩa.
• Các đường chéo chia đôi các góc.
• Các đường chéo trong một cánh diều chia đôi nhau thành các góc vuông.

Tính chất của tứ giác

Các tính chất của tứ giác bao gồm:

• Tứ giác nào cũng có 4 cạnh, 4 đỉnh và 4 góc.4
• Tổng số đo của tất cả bốn góc trong của một hình tứ giác luôn bằng 360 độ
• Tổng các góc trong của một tứ giác phù hợp với công thức của đa giác tức là

Tổng các góc trong = 180 ° * (n – 2), trong đó n bằng số cạnh của đa giác

• Hình chữ nhật, hình thoi và hình vuông đều là một dạng của hình bình hành.
• Hình vuông vừa là hình thoi vừa là hình chữ nhật
• Hình chữ nhật và hình thoi không phải là hình vuông.
• Hình bình hành là hình thang.
• Hình thang không phải là hình bình hành.
• Cánh diều không phải là hình bình hành.

Phân loại tứ giác

Các tứ giác được phân thành hai loại cơ bản:

• Tứ giác lồi: Là tứ giác có góc trong nhỏ hơn 180 độ và hai đường chéo nằm trong tứ giác. Chúng bao gồm hình thang, hình bình hành, hình thoi, hình chữ nhật, hình vuông, hình cánh diều, v.v.
• Tứ giác lõm: Là tứ giác có ít nhất một góc trong lớn hơn 180 độ và ít nhất một trong hai đường chéo nằm ngoài tứ giác. Một chiếc phi tiêu là một tứ giác lõm.

Có một loại tứ giác khác ít phổ biến hơn, được gọi là tứ giác phức tạp. Đây là những con số chéo. Ví dụ: hình thang chéo, hình chữ nhật chéo, hình vuông chéo, v.v.

Hãy làm một vài bài toán ví dụ về tứ giác.

ví dụ 1

Các góc trong của một tứ giác không đều là; x °, 80 °, 2x ° và 70 °. Tính giá trị của x.

Giải pháp

Theo tính chất của tứ giác (Tổng các góc trong = 360 °), chúng ta có,

⇒ x ° + 80 ° + 2x ° + 70 ° = 360 °

Đơn giản hóa.

⇒ 3x + 150 ° = 360 °

Trừ 150 ° cho cả hai bên.

⇒ 3x + 150 ° – 150 ° = 360 ° – 150 °

⇒ 3x = 210 °

Chia cả hai vế cho 3 để được;

⇒ x = 70 °

Do đó, giá trị của x là 70 °

Và các góc của các tứ giác là; 70 °, 80 °, 140 ° và 70 °.

Xem thêm:

Diện tích hình vuông – Giải thích & Ví dụ đơn giản nhanh chóng

Tính diện tích Vùng bóng mờ dễ hiểu nhất hiện nay

Ví dụ 2

Các góc trong của một tứ giác là; 82 °, (25x – 2) °, (20x – 1) ° và (25x + 1) ° Tìm các góc của tứ giác.

Giải pháp

Tổng các góc trong của một tứ giác = 360 °

⇒ 82 ° + (25x – 2) ° + (20x – 1) ° + (25x + 1) ° = 360 °

⇒ 82 + 25x – 2 + 20x – 1 + 25x + 1 = 360

Đơn giản hóa.

⇒ 70x + 80 = 360

Trừ cả hai bên đi 80 để được;

⇒ 70x = 280

Chia cả hai bên cho 70.

⇒ x = 4

Bằng cách thay thế,

⇒ (25x – 2) = 98 °

⇒ (20x – 1) = 79 °

⇒ (25x + 1) = 101 °

Do đó, các góc của tứ giác là; 82 °, 98 °, 79 ° và 101 °.

Câu hỏi thực hành

1. Hãy xem xét một hình bình hành PQRS, trong đó
2. Tìm 4 góc trong của hình thoi có cạnh và một trong các đường chéo có độ dài bằng nhau.

Câu trả lời

1. <P, 110 °,
2. 60 °, 60 °, 120 ° và ° 120.