Cách thực hiện Vectơ trực giao chuẩn không cần chỉnh

Trong lĩnh vực hình học vectơ, chúng ta đã đề cập đến hầu hết mọi khái niệm về vectơ. Chúng tôi đã đề cập đến vectơ thông thường, phương trình vectơ, sản phẩm chấm vectơ, và nhiều loại khác. Nhưng một trong những khái niệm quan trọng nhất trong lĩnh vực này là sự hiểu biết về một vectơ trực giao. 

Các vectơ trực giao được định nghĩa là:

“2 vectơ được gọi là trực giao nếu chúng vuông góc với nhau và sau khi thực hiện phân tích tích điểm, sản phẩm mà chúng mang lại bằng không.”

Trong chủ đề này, chúng tôi sẽ tập trung vào các lĩnh vực sau:

• Vectơ trực giao là gì?
• Làm thế nào để tìm vectơ trực giao?
• Tính chất của vectơ trực giao là gì?
• Các ví dụ
• Thực hành các vấn đề

Vectơ trực giao là gì? 

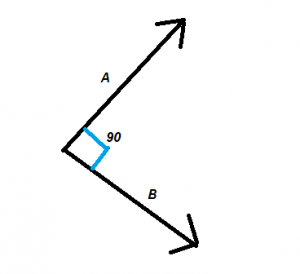
Theo thuật ngữ toán học, từ trực giao có nghĩa là hướng vào một góc 90 °. Hai vectơ u, v trực giao với nhau nếu chúng vuông góc, tức là chúng tạo thành một góc vuông, hoặc nếu tích chấm mà chúng mang lại bằng không .

Vì vậy, chúng ta có thể nói ,

u⊥v hoặc u · v = 0

Do đó, tích số chấm được sử dụng để xác nhận xem hai vectơ nghiêng cạnh nhau có hướng với nhau một góc 90 ° hay không.

Nếu chúng ta đi sâu vào các tính chất của vectơ trực giao, chúng ta sẽ biết rằng vectơ 0, về cơ bản là số 0, thực tế là trực giao với mọi vectơ. Chúng ta có thể xác nhận điều này vì u.0 = 0 với bất kỳ vectơ u nào , vectơ 0 là trực giao với mọi vectơ. Điều này là do vectơ không bằng 0 và rõ ràng sẽ tạo ra kết quả rỗng hoặc 0 khi được nhân với bất kỳ số nào hoặc bất kỳ vectơ nào.

Hai vectơ u và y trong không gian tích bên trong, V, là trực giao nếu tích bên trong của chúng bằng 0

(u, y) = 0

Bây giờ chúng ta biết rằng tích số chấm là chìa khóa chính để tìm ra liệu 2 vectơ có trực giao hay không, chúng ta hãy tiến hành một số ví dụ để hiểu rõ hơn.

ví dụ 1

Kiểm tra xem các vectơ a = i + 2j và b = 2i – j có trực giao hay không.

Giải pháp

Để kiểm tra xem 2 vectơ có trực giao hay không, chúng tôi sẽ tính tích số chấm của các vectơ này:

ab = (1 · 2) + (2 · (-1))

ab = 2 – 2

ab = 0 

Do đó, vì tích số chấm bằng 0, nên hai vectơ là trực giao.

Ví dụ 2

Các vectơ  a  = (3, 2) và  b  = (7, -5} có trực giao với nhau không?

Giải pháp

Để kiểm tra xem 2 vectơ có trực giao hay không, chúng tôi sẽ tính tích số chấm của các vectơ này:

ab = (3,7) + (7. (-5))

ab = 21 – 35

ab = -14

Vì tích chấm của 2 vectơ này không phải là số 0 nên các vectơ này không trực giao với nhau.

Làm thế nào để tìm một vectơ trực giao?

Chúng ta đã thảo luận rằng một cách để tìm các vectơ trực giao là kiểm tra tích số chấm của chúng. Nếu tích số chấm cho ra câu trả lời bằng không, thì rõ ràng là các vectơ đang được nhân thực sự là trực giao hoặc vuông góc. 

Chung có thể được sử dụng trong vấn đề này như sau:

ab = 0 

Khái niệm này cũng có thể được mở rộng dưới dạng các thành phần vectơ.

Trong trường hợp này, phương trình tổng quát sẽ trở thành một cái gì đó giống như sau:

ab = (ax.bx) + (ay.by)

ab = 0

Do đó, yêu cầu chính của vectơ để trực giao là chúng phải luôn cung cấp một tích số chấm cho chúng ta kết quả bằng không.

Nhưng chúng ta cũng hãy xem xét một số kịch bản và phương pháp luận khác.

2 vectơ được nhân có thể tồn tại trong bất kỳ mặt phẳng nào. Không có hạn chế nào đối với chúng chỉ giới hạn trong các mặt phẳng hai chiều. Vì vậy, chúng ta hãy mở rộng nghiên cứu của chúng ta sang các mặt phẳng ba chiều.

Véc tơ trực giao trong trường hợp mặt phẳng hai chiều

Hầu hết các bài toán trong toán học bị giới hạn trong các mặt phẳng hai chiều. Một mặt phẳng như vậy chỉ tồn tại 2 trục, đó là trục x và trục y. Trong phần vectơ đơn vị, chúng ta cũng đã thảo luận rằng các trục này cũng có thể được biểu diễn dưới dạng vectơ đơn vị; trục x ở dạng vectơ đơn vị i và trục y ở dạng vectơ đơn vị j.

Bây giờ, chúng ta hãy xem xét rằng có 2 vectơ, tên là a và b , tồn tại trong một mặt phẳng hai chiều. Chúng ta phải kiểm chứng xem hai vectơ này có trực giao với nhau hay không, nói cách khác là có vuông góc với nhau hay không.

Chúng tôi đã kết luận rằng để kiểm tra tính trực giao, chúng tôi đánh giá tích số chấm của các vectơ tồn tại trong mặt phẳng. Vì vậy, tích chấm của vectơ a và b sẽ là một cái gì đó như được hiển thị bên dưới:

ab = | a | x | b | x cosθ

Nếu 2 vectơ trực giao hoặc vuông góc thì góc θ giữa chúng sẽ là 90 °.

Như chúng ta biết,

cosθ = cos 90 °

Và,

cos 90 ° = 0

Vì vậy, chúng ta có thể viết lại phương trình tích điểm thành:

ab = | a | x | b | x cos 90 °

ab = 0

Chúng ta cũng có thể biểu thị hiện tượng này dưới dạng thành phần véc tơ.

ab = ax.bx + ay.by

Và chúng tôi đã đề cập ở trên rằng trong điều kiện biểu diễn trên cơ sở các vectơ đơn vị; chúng ta có thể sử dụng các ký tự i và j.

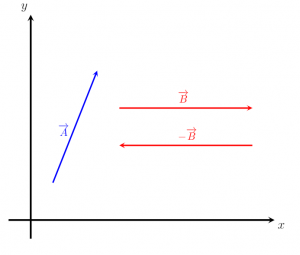
Vì thế,

ab = ai.bi + aj.bj 

ab = 0

Do đó, nếu tích dấu chấm cũng cho kết quả là số 0 trong trường hợp nhân các thành phần, thì 2 vectơ là trực giao.

Ví dụ 3

Tìm xem các vectơ a = (5, 4) và b = (8, -10) có trực giao với nhau hay không.

Giải pháp

Để kiểm tra xem 2 vectơ có trực giao hay không, chúng tôi sẽ tính tích số chấm của các vectơ này:

ab = ai.bi + aj.bj

ab = (5,8) + (4. -10)

ab = 40 – 40

ab = 0

Do đó, người ta chứng minh rằng hai vectơ trực giao về bản chất.

Ví dụ 4

Tìm xem các vectơ a = (2, 8) và b = (12, -3) có trực giao với nhau hay không.

Giải pháp: 

Để kiểm tra xem 2 vectơ có trực giao hay không, chúng tôi sẽ tính tích số chấm của các vectơ này:

ab = ai.bi + aj.bj

ab = (2.12) + (8. -3)

ab = 24 – 24

ab = 0

Do đó, người ta chứng minh rằng hai vectơ trực giao về bản chất.

Véc tơ trực giao trong trường hợp mặt phẳng ba chiều

Hầu hết các bài toán trong cuộc sống thực đều yêu cầu các vectơ thoát ra trong một mặt phẳng ba chiều. Khi chúng ta nói về mặt phẳng ba chiều, chúng ta đi kèm với một trục khác, đó là trục z.

Trong trường hợp này, với việc bao gồm trục thứ ba, trục z sẽ bao gồm 3 thành phần, mỗi thành phần hướng dọc theo trục tương ứng của nó nếu chúng ta nói rằng bất kỳ vectơ nào tồn tại trong một mặt phẳng ba chiều. Trong trường hợp này, 3 thành phần của một vectơ trong mặt phẳng ba chiều sẽ là thành phần x, thành phần y và thành phần z.

Nếu chúng ta biểu diễn các thành phần này dưới dạng vectơ đơn vị, thì chúng ta đã biết rằng đối với trục x và y, chúng ta sử dụng các ký tự i và j để biểu diễn các thành phần của chúng. Nhưng bây giờ chúng ta có một trục thứ ba và đồng thời là thành phần thứ ba, chúng ta cần một biểu diễn thứ ba bổ sung.

Vì vậy, đối với trục thứ ba này, chúng ta sử dụng ký tự k để biểu diễn vector đơn vị dọc theo trục z.

Bây giờ, hãy xem xét rằng 2 vectơ tồn tại trong một mặt phẳng ba chiều. Các vectơ này rõ ràng sẽ có 3 thành phần và tích số chấm của các vectơ như vậy có thể được tìm thấy bên dưới:

ab = ax.bx + ay.by + az.bz

Hoặc, theo nghĩa của vectơ đơn vị i, j và k :

ab = ai.bi + aj.bj + ak.bk

ab = 0

Do đó, nếu kết quả này cho ra một tích số 0, thì chúng ta sẽ có thể kết luận rằng 2 vectơ trong một mặt phẳng ba chiều về bản chất là vuông góc hoặc trực giao.

Ví dụ 5

Kiểm tra xem các vectơ a = (2, 3, 1) và b = (3, 1, -9) có trực giao hay không.

Giải pháp

Để kiểm tra xem 2 vectơ này có trực giao hay không, chúng ta sẽ tính tích số chấm của chúng. Vì 2 vectơ này có 3 thành phần nên chúng tồn tại trong một mặt phẳng ba chiều.

Vì vậy, chúng ta có thể viết: ab = ai.bi + aj.bj + ak.bk

Bây giờ, đặt các giá trị trong công thức:

ab = (2.3) + (3.1) + (1. -9)

ab = 6 + 3 -9

ab = 0

Vì tích số chấm bằng 0, do đó 2 vectơ này trong mặt phẳng ba chiều về bản chất là trực giao.

Ví dụ 6

Tìm xem 2 vectơ a = i + 2j và b = 2i -j + 10k có trực giao với nhau hay không.

Giải pháp

Để kiểm tra xem 2 vectơ này có trực giao hay không, chúng ta sẽ tính tích số chấm của chúng. Vì 2 vectơ này có 3 thành phần nên chúng tồn tại trong một mặt phẳng ba chiều.

Vì vậy, chúng ta có thể viết: ab = ai.bi + aj.bj + ak.bk

Bây giờ, đặt các giá trị trong công thức:

ab = (1.2) + (2. -1) + (0.10)

ab = 2 -2 + 0

ab = 0

Vì tích số chấm bằng 0, do đó 2 vectơ này trong mặt phẳng ba chiều về bản chất là trực giao.

Ví dụ 7

Kiểm tra xem 2 vectơ a = (2, 4, 1) và b = (2, 1, -8) có trực giao với nhau hay không.

Giải pháp

Để kiểm tra xem 2 vectơ này có trực giao hay không, chúng ta sẽ tính tích số chấm của chúng. Vì 2 vectơ này có 3 thành phần nên chúng tồn tại trong một mặt phẳng ba chiều.

Vì vậy, chúng ta có thể viết:

ab = ai.bi + aj.bj + ak.bk

Bây giờ, đặt các giá trị trong công thức:

ab = (2.2) + (4.1) + (1. -8)

ab = 4 + 4 – 8

ab = 0

Vì tích số chấm bằng 0, do đó 2 vectơ này trong mặt phẳng ba chiều về bản chất là trực giao.

Thuộc tính của vectơ trực giao

Bây giờ chúng ta đã xem qua tất cả các thông tin cần thiết của vectơ trực giao và hiểu rõ về cách kiểm tra xem vectơ có trực giao hay không, sau đây chúng ta hãy phân tích một số tính chất của vectơ trực giao.

Vuông góc trong tự nhiên

Các vectơ được cho là trực giao sẽ luôn vuông góc về bản chất và sẽ luôn mang lại tích số chấm là 0 vì nếu vuông góc có nghĩa là chúng sẽ có một góc 90 ° giữa chúng.

Vectơ Zero là trực giao

Vectơ 0 sẽ luôn trực giao với mọi vectơ mà vectơ 0 tồn tại cùng. Điều này là do bất kỳ vectơ nào, khi được nhân với vectơ 0, sẽ luôn mang lại tích số chấm bằng 0.

Sản phẩm chéo của các vectơ trực giao

Tích chéo của 2 vectơ trực giao không bao giờ có thể bằng không. Điều này là do công thức tích chéo liên quan đến hàm lượng giác sin, và sin 90 ° luôn bằng 1. Do đó tích chéo của các vectơ trực giao sẽ không bao giờ bằng 0.

Vấn đề thực hành:

1. Tìm xem các vectơ (1, 2) và (2, -1) có trực giao với nhau hay không.
2. Tìm xem các vectơ (1, 0, 3) và (4, 7, 4) có trực giao với nhau hay không.
3. Chứng minh rằng tích chéo của các vectơ trực giao không bằng không.

Câu trả lời

1. Đúng
2. Không
3. Chứng minh qua công thức tích chéo

Xem thêm:

Cách giải Vectơ Phủ định nhanh chóng chi tiết nhất

Vectơ song song và những điều bạn chưa biết