Những thông tin cần biết về vectơ vị trí

Chúng ta có thể sử dụng một vectơ vị trí để cho chúng ta biết vị trí của một đối tượng này so với một đối tượng khác. Cụ thể, một vectơ vị trí là:

“Một vectơ cho biết vị trí hoặc vị trí của một điểm nhất định đối với một điểm tham chiếu tùy ý chẳng hạn như điểm gốc.”

Trong chủ đề này, chúng ta sẽ thảo luận về các khía cạnh sau của vectơ vị trí:

• Vectơ vị trí là gì?
• Cách tìm vectơ vị trí

Vectơ vị trí là gì? 

Thông thường, các vectơ bắt đầu tại điểm gốc và kết thúc tại bất kỳ điểm tùy ý nào được gọi là vectơ vị trí. Chúng được sử dụng để xác định vị trí của một điểm có tham chiếu đến điểm gốc.

Hướng của vectơ vị trí từ gốc tọa độ đối với điểm đã cho. Trong hệ tọa độ Descartes, nếu điểm O là điểm gốc và Q là điểm nào đó (x1, y1), thì vectơ vị trí hướng từ điểm O đến điểm Q được biểu diễn là OQ . Trong không gian ba chiều, nếu O = (0,0,0) và Q = (x1, y1, z1) thì vectơ vị trí r của điểm Q được biểu diễn là:

r = x1i + y1j + z1k

Giả sử chúng ta có hai vectơ A và B với các vectơ vị trí lần lượt là a = (2,4) và b = (3, 5). Sau đó, chúng ta có thể viết tọa độ của các vectơ A và B là:

A = (2,4), B = (3, 5)

Cách tìm vectơ vị trí

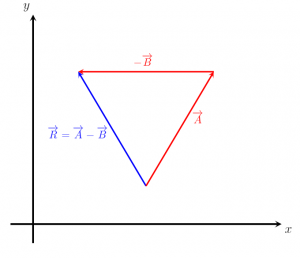
Trước khi xác định vectơ vị trí của một điểm, trước hết chúng ta cần xác định tọa độ của điểm đó. Giả sử chúng ta có hai điểm, M và N, trong đó M = (x1, y1) và N = (x2, y2). Tiếp theo, chúng ta muốn tìm vectơ vị trí từ điểm M đến điểm N, vectơ MN . Để xác định véc tơ vị trí này, chúng tôi loại trừ các thành phần tương ứng của M từ N :

MN = (x2-x1, y2-y1)

Công thức vectơ vị trí

Sử dụng thông tin trên, chúng ta có thể tổng quát một công thức sẽ xác định một vectơ vị trí giữa hai điểm nếu chúng ta biết vị trí của các điểm trong mặt phẳng xy.

Ví dụ, hãy xem xét một điểm P, có tọa độ (xk, yk) trong mặt phẳng xy và một điểm khác Q, có tọa độ (xk + 1, yk + 1). Công thức xác định vectơ vị trí từ P đến Q là:

PQ = ((xk + 1) -xk, (yk + 1) -yk)

Hãy nhớ vectơ vị trí PQ dùng để chỉ một vectơ bắt đầu tại điểm P và kết thúc tại điểm Q. Tương tự, nếu chúng ta muốn tìm vectơ vị trí từ điểm Q đến điểm P, chúng ta có thể viết:

QP = (xk – (xk + 1), yk – (yk + 1))

Các ví dụ 

Trong phần này, chúng ta sẽ thảo luận về một số bài toán ví dụ vectơ vị trí và các giải pháp từng bước của chúng. Điều này sẽ giúp hiểu sâu hơn về vectơ vị trí.

 ví dụ 1

Cho hai điểm A = (-4, 6) và B = (5, 12), hãy xác định vectơ vị trí AB. Sau đó , tính độ lớn của vectơ AB .

Giải pháp

Cho hai điểm trong hệ tọa độ xy, ta có thể sử dụng công thức sau để tìm vectơ vị trí AB :

AB = (x2-x1, y2-y1)

Trong đó x1, y1 đại diện cho tọa độ điểm A và x2, y2 đại diện cho tọa độ điểm B. Do đó, chỉ cần đặt các giá trị của điểm A và B vào phương trình trên, chúng ta có thể tìm được vectơ vị trí AB :

AB = (5 – (- 4), 12-6)

AB = ((5+ 4), 12-6)

AB = (9, 6)

Do đó, vectơ vị trí AB tương đương với một vectơ bắt đầu tại gốc và hướng đến một điểm 9 đơn vị ở bên phải dọc theo trục x và 6 đơn vị hướng lên dọc theo trục y.

Tiếp theo, chúng tôi xác định độ lớn của vectơ vị trí như sau:

| AB | = √9 ^ 2 + 6 ^ 2

| AB | = √81 + 36

| AB | = √117

| AB | = 3√13 

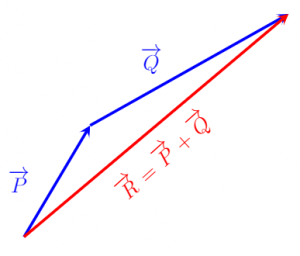
Ví dụ 2

Cho hai điểm A = (-4, 6) và B = (5, 12), xác định vectơ vị trí BA. Sau đó, tính độ lớn của vectơ BA và mô tả mối quan hệ giữa vectơ vị trí AB và vectơ vị trí BA .

Giải pháp

Cho hai điểm trong hệ tọa độ xy, ta có thể sử dụng công thức sau để tìm vectơ vị trí BA :

BA = (x1-x2, y1-y2)

Trong đó x1, y1 đại diện cho tọa độ điểm A và x2, y2 đại diện cho tọa độ điểm B. Lưu ý rằng vectơ vị trí BA biểu thị một vectơ hướng từ điểm B đến điểm A. Nó khác với vectơ vị trí AB,  hướng từ A đến B. Do đó, chỉ cần đặt các giá trị của điểm A và B vào phương trình trên , chúng ta có thể tìm thấy vectơ vị trí BA:

BA = (-4-5), 6-12)

BA = (-9, -6)

Do đó, vectơ vị trí BA tương đương với một vectơ bắt đầu tại điểm gốc và hướng đến một điểm 9 đơn vị ở bên trái dọc theo trục x và 6 đơn vị hướng xuống dọc theo trục y.

Tiếp theo, chúng tôi xác định độ lớn của vectơ vị trí:

| BA | = √ (-9) ^ 2 + (-6) ^ 2

| BA | = √81 + 36

| BA | = √117

| BA | = 3√13

Nhớ lại rằng trong ví dụ đầu tiên, chúng ta tìm vectơ vị trí AB cho các điểm giống nhau và trong ví dụ này, chúng tôi xác định vectơ vị trí BA. Hai vectơ vị trí có cùng độ lớn. Vì chúng có hướng ngược nhau, mối quan hệ giữa hai là:

BA = -1 * (9, 6)

BA = -1 * AB

BA = – AB

Như vậy, hai vectơ vị trí song song với nhau và đối nhau. Tức là chúng là phủ định của nhau.

Ví dụ 3

Cho rằng vectơ vị trí của một điểm, S1, là OS1 = (2, 3) và vectơ S1S2 = (-3, 6), hãy xác định vectơ vị trí của điểm S2, OS2 .

Giải pháp

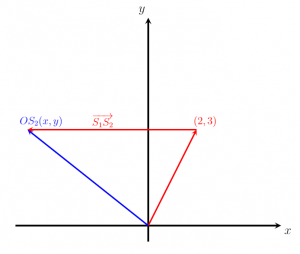
Đầu tiên, chúng tôi vẽ vector OS1 với điểm ban đầu của nó tại điểm gốc, (0,0) và điểm cuối của nó tại (2,3). Chúng tôi cũng vẽ vector OS2, bắt đầu tại điểm gốc và kết thúc tại điểm S2. Ta sẽ chỉ định vị trí chưa biết của S2 với các điểm tọa độ tùy ý (x, y). Vì chúng ta biết vectơ vị trí S1S2 và chúng ta biết rằng nó cung cấp mối quan hệ giữa S1 và S2, chúng ta cũng có thể vẽ S1S2. Nó là một vectơ hướng có điểm ban đầu là S1 và hướng sang trái ba đơn vị và hướng lên sáu đơn vị. Rõ ràng là từ hình ảnh dưới đây, chúng ta có một hình tam giác, 0S1S2. Vì vậy, bây giờ chúng ta có thể sử dụng định luật tam giác (hoặc quy tắc đầu-đuôi) của phép cộng vectơ để xác định tọa độ của điểm S2 như sau:

S1S2 = OS1 + OS2

OS2 = S1S2 – OS1

Bằng cách đặt các giá trị đã cho vào phương trình này, chúng ta nhận được:

OS2 = (-3, 6) – (2, 3)

OS2 = (-3, 6) + (-2, -3)

OS2 = (-3-2, 6-3)

OS2 = (-5, 3)

Do đó, OS2 = (- 5, 3) là vectơ vị trí của điểm S2.

Ví dụ 4

Cho hai điểm M = (4, m) và Q = (-n, -3), xác định vectơ vị trí QM.

Giải pháp

Cho hai điểm trong hệ tọa độ xy, ta có thể sử dụng công thức sau để xác định vectơ vị trí Q :

QM = (-n-4, -3-m).

Vì chúng ta không biết tọa độ của QM hoặc giá trị của n và m nên chúng ta không thể đơn giản hóa phương trình.

Ví dụ 5

Cho điểm q = (-10, 5, 3), xác định vectơ vị trí của điểm q, R. Sau đó xác định hoành độ của R.

Giải pháp

Cho điểm q, chúng ta có thể xác định vectơ vị trí của nó:

R = -10i + 5j -3k.

Để xác định độ lớn của nó, chúng tôi sử dụng phương trình sau:

| R | = √ (-10) ^ 2 + (5) ^ 2 + (-3) ^ 2

| R | = √100 + 25 + 9

| R | = √100 + 25 + 9

| R | = √134

Ví dụ 6

Cho các điểm c = 5i + 6j + 3k và d = 2i + 5j – 2k trong hệ trực giao, hãy xác định vectơ vị trí giữa hai điểm này, CD.

Giải pháp

Cho hai điểm, chúng ta có thể sử dụng công thức sau để xác định vị trí vectơ CD :

CD = (2-5, 5-5, -2-3)

CD = (-3, 0, -5)

CD = -3i + 0j -5k

Câu hỏi thực hành

1. Cho u = (-1, 4) và v = (2, 5). Xác định vectơ vị trí được biểu diễn bởi UV .
2. Cho u = (-1, 4) và v = (2, 5). Xác định vectơ vị trí biểu diễn bởi VU .
3. Cho v = (3, 5) và VM = (-6, 3). Tìm vectơ vị trí của điểm m.
4. Cho b = (3,2,5), xác định vectơ vị trí của nó, R. Sau đó, tìm độ dài của vectơ
5. Cho vectơ AB bắt đầu tại a = (1, 2) và kết thúc tại b = (2, 3). Xác định vectơ vị trí và độ dài của nó.
6. Cho một vectơ OB bắt đầu tại o = (0,0) và kết thúc tại b = (-2, 6). Xác định vectơ vị trí của nó.

Câu trả lời

1. UV = (3,1). Hướng của tia UV là 3 đơn vị sang phải dọc theo trục x và 1 đơn vị lên trên.
2. VU = (-3, -1). Hướng của VU là 3 đơn vị sang trái dọc theo trục x và 1 đơn vị xuống dưới. Hai vectơ UV và VU ngược hướng.
3. Vectơ vị trí của điểm m có thể cho OM = (-9, -2)
4. R = 3i + 2j + 5k là vectơ vị trí, và độ dài của nó là | R | = √38
5. Vectơ vị trí là AB = (1,1), và độ dài của nó là | AB | = √2
6. Vectơ vị trí là OB = (-2,6), và độ dài của nó là | OB | = √40

Xem thêm:

Vectơ song song và những điều bạn chưa biết

Cách thực hiện Vectơ trực giao chuẩn không cần chỉnh