Định hướng Cosines & Tỷ lệ hướng của một đường
Contents
Định nghĩa xác suất trong toán học
Xác suất là thước đo khả năng xảy ra một sự kiện. Nhiều sự kiện không thể được dự đoán một cách chắc chắn. Chúng ta chỉ có thể dự đoán cơ hội của một sự kiện xảy ra tức là khả năng chúng xảy ra như thế nào, bằng cách sử dụng nó. Xác suất có thể nằm trong khoảng từ 0 đến 1, trong đó 0 có nghĩa là sự kiện không thể xảy ra và 1 chỉ ra một sự kiện nhất định. Xác suất lớp 10 là một chủ đề quan trọng đối với học sinh, nó giải thích tất cả các khái niệm cơ bản của chủ đề này. Xác suất của tất cả các sự kiện trong không gian mẫu cộng lại bằng 1.
Ví dụ , khi chúng ta tung một đồng xu, hoặc chúng ta nhận được Đầu HOẶC Đuôi, chỉ có thể có hai kết quả có thể xảy ra (H, T). Nhưng nếu chúng ta tung hai đồng xu lên không trung, có thể có ba khả năng xảy ra sự kiện, chẳng hạn như cả hai đồng xu đều hiển thị đầu hoặc cả hai đều hiển thị đuôi hoặc một đồng xu hiển thị đầu và một đuôi, tức là (H, H), (H, T ), (T, T).
Công thức xác suất
Công thức xác suất được định nghĩa là khả năng xảy ra một sự kiện bằng tỷ số giữa số kết quả thuận lợi và tổng số kết quả.
| Xác suất sự kiện xảy ra P (E) = Số kết quả thuận lợi / Tổng số kết quả |
Đôi khi học sinh bị nhầm lẫn giữa “kết quả thuận lợi” với “kết quả mong muốn”. Đây là công thức cơ bản. Nhưng có một số công thức khác cho các tình huống hoặc sự kiện khác nhau.
Ví dụ và giải pháp
1) Trên giường có 6 cái gối, 3 cái màu đỏ, 2 cái màu vàng và 1 cái màu xanh lam. Xác suất chọn được một chiếc gối màu vàng là bao nhiêu?
Trả lời: Xác suất bằng số gối màu vàng trên giường chia cho tổng số gối, tức là 2/6 = 1/3.
2) Có một hộp đựng đầy các lọ màu đỏ, xanh lam, xanh lục và cam. Một số chai được lấy ra và di dời. Sumit đã làm điều này 1000 lần và nhận được kết quả như sau:
- Số chai màu xanh lam được chọn ra: 300
- Số chai màu đỏ: 200
- Số chai màu xanh lá cây: 450
- Số chai màu cam: 50
a) Tính xác suất để Sumit chọn được một chai màu xanh lá cây?
Trả lời: Cứ 1000 chai được lấy ra thì có 450 chai có màu xanh.
Do đó, P (xanh lục) = 450/1000 = 0,45
b) Nếu có 100 chai trong thùng thì có bao nhiêu chai có khả năng còn xanh?
Trả lời: Thí nghiệm ngụ ý rằng 450 trong số 1000 chai có màu xanh.
Do đó, trong số 100 chai, 45 chai có màu xanh.
Cây xác suất
Các sơ đồ cây giúp tổ chức và hình dung ra kết quả khác nhau càng tốt. Cành và ngọn cây là hai vị trí chính. Xác suất của mỗi nhánh được viết trên nhánh, trong khi các phần cuối chứa kết quả cuối cùng. Sơ đồ cây được sử dụng để tìm ra khi nào cần nhân và khi nào cần thêm. Bạn có thể xem bên dưới một sơ đồ cây cho đồng tiền:


Các loại xác suất
Có ba loại xác suất chính:
- Xác suất lý thuyết
- Xác suất thử nghiệm
- Xác suất tiên đề
Xác suất lý thuyết
Nó dựa trên khả năng có thể xảy ra một điều gì đó. Xác suất lý thuyết chủ yếu dựa trên lý luận đằng sau xác suất. Ví dụ, nếu một đồng xu được tung, xác suất lý thuyết để nhận được một đầu sẽ là ½.
Xác suất thử nghiệm
Nó dựa trên cơ sở của những quan sát của một thí nghiệm. Các khả năng thực nghiệm có thể được tính toán dựa vào số lượng các kết quả có thể bằng tổng số lần thử. Ví dụ, nếu một đồng xu được tung 10 lần và các mặt ngửa được ghi lại 6 lần thì xác suất thực nghiệm cho các mặt ngửa là 6/10 hoặc 3/5.
Xác suất tiên đề
Trong xác suất tiên đề, một tập hợp các quy tắc hoặc tiên đề được thiết lập áp dụng cho tất cả các loại. Những tiên đề này do Kolmogorov đặt ra và được gọi là ba tiên đề của Kolmogorov. Với cách tiếp cận tiên đề về xác suất, cơ hội xảy ra hoặc không xảy ra của các sự kiện có thể được định lượng. Các khả năng tiên đề bài học bao gồm khái niệm này một cách chi tiết với Kolmogorov của ba quy tắc (tiên đề) cùng với các ví dụ khác nhau.
Xác suất có điều kiện là khả năng xảy ra một sự kiện hoặc kết quả dựa trên sự xuất hiện của một sự kiện hoặc kết quả trước đó.
Xác suất của một sự kiện
Giả sử một sự kiện E có thể xảy ra theo r cách trong tổng số n cách có thể xảy ra hoặc có thể xảy ra như nhau . Khi đó xác suất xảy ra của sự kiện hoặc sự thành công của nó được biểu thị bằng;
P (E) = r / n
Xác suất mà sự kiện sẽ không xảy ra hoặc được gọi là sự cố của nó được biểu thị như sau:
P (E ‘) = (nr) / n = 1- (r / n)
E ‘biểu thị rằng sự kiện sẽ không xảy ra.
Do đó, bây giờ chúng ta có thể nói;
P (E) + P (E ‘) = 1
Điều này có nghĩa là tổng tất cả các xác suất trong bất kỳ thử nghiệm hoặc thử nghiệm ngẫu nhiên nào đều bằng 1.
Các sự kiện có khả năng xảy ra ngang nhau là gì?
Khi các sự kiện có cùng xác suất xảy ra theo lý thuyết, thì chúng được gọi là các sự kiện có khả năng xảy ra như nhau. Các kết quả của không gian mẫu được gọi là có khả năng xảy ra như nhau nếu tất cả chúng đều có cùng xác suất xảy ra. Ví dụ, nếu bạn ném một con súc sắc, thì xác suất nhận được 1 là 1/6. Tương tự, xác suất lấy được tất cả các số từ 2,3,4,5 và 6 lần lượt là 1/6. Do đó, sau đây là một số ví dụ về các sự kiện có khả năng xảy ra tương đương khi ném một con súc sắc:
- Bắt 3 và 5 khi ném xúc xắc
- Lấy một số chẵn và một số lẻ trên xúc xắc
- Bắt 1, 2 hoặc 3 khi lăn một con súc sắc
là các sự kiện có khả năng xảy ra như nhau, vì xác suất của mỗi sự kiện là bằng nhau.
Sự kiện bổ sung
Khả năng chỉ có hai kết quả nói lên rằng một sự kiện sẽ xảy ra hoặc không. Giống như một người sẽ đến hoặc không đến nhà bạn, nhận được việc làm hoặc không nhận được việc làm, v.v. là những ví dụ về các sự kiện bổ sung cho nhau. Về cơ bản, phần bổ sung của một sự kiện xảy ra hoàn toàn ngược lại với khả năng nó không xảy ra. Một số ví dụ khác là:
- Hôm nay trời sẽ mưa hoặc không mưa
- Học sinh sẽ vượt qua kỳ thi hoặc không đậu.
- Bạn trúng số hoặc không.
Lý thuyết xác suất
Lý thuyết xác suất bắt nguồn từ thế kỷ 16 khi J.Cardan, một nhà toán học và bác sĩ người Ý, đề cập đến công trình đầu tiên về chủ đề này, Cuốn sách về các trò chơi may rủi. Sau khi ra đời, kiến thức về xác suất đã thu hút sự chú ý của các nhà toán học vĩ đại. Vì vậy, lý thuyết Xác suất là một nhánh của toán học đề cập đến khả năng xảy ra của các sự kiện. Mặc dù có nhiều cách giải thích xác suất riêng biệt, lý thuyết xác suất giải thích khái niệm một cách chính xác bằng cách diễn đạt nó thông qua một tập hợp các tiên đề hoặc giả thuyết. Các giả thuyết này giúp hình thành xác suất trong không gian khả năng, cho phép một thước đo giữ các giá trị từ 0 đến 1. Đây được gọi là thước đo xác suất, cho một tập hợp các kết quả có thể có của không gian mẫu.
Hàm mật độ xác suất
Hàm mật độ xác suất (PDF) là hàm xác suất được biểu thị cho mật độ của một biến ngẫu nhiên liên tục nằm giữa một phạm vi giá trị nhất định. Hàm mật độ xác suất giải thích phân phối chuẩn và giá trị trung bình và độ lệch tồn tại như thế nào. Phân phối chuẩn chuẩn được sử dụng để tạo cơ sở dữ liệu hoặc thống kê, thường được sử dụng trong khoa học để biểu diễn các biến có giá trị thực, mà phân phối của chúng chưa được biết đến
Các thuật ngữ và định nghĩa xác suất
Một số thuật ngữ xác suất quan trọng được thảo luận ở đây:
| Kỳ hạn | Định nghĩa | Thí dụ |
|---|---|---|
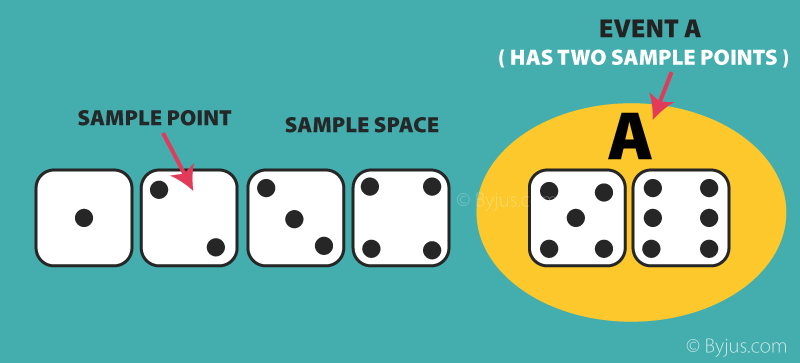
| Không gian mẫu | Tập hợp tất cả các kết quả có thể xảy ra trong bất kỳ thử nghiệm nào |
|
| Điểm mẫu | Đó là một trong những kết quả có thể | Trong một bộ bài:
|
| Thử nghiệm hoặc Thử nghiệm | Một loạt các hành động mà kết quả luôn không chắc chắn. | Việc tung đồng xu, Chọn một lá bài từ bộ bài, ném một con xúc xắc. |
| Biến cố | Đó là một kết quả duy nhất của một thử nghiệm. | Nhận được Thủ lĩnh trong khi tung đồng xu là một sự kiện. |
| Kết quả | Kết quả có thể có của một thử nghiệm / thử nghiệm | T (đuôi) là kết quả có thể xảy ra khi tung đồng xu. |
| Sự kiện miễn phí | Các sự kiện không xảy ra. Phần bù của một sự kiện A là sự kiện, không phải A (hoặc A ‘) | Bộ bài tiêu chuẩn 52 lá, A = Vẽ một trái tim, sau đó A ‘= Không vẽ một trái tim |
| Sự kiện bất khả thi | Sự kiện không thể xảy ra | Khi tung đồng xu, không thể lấy cả đầu và đuôi cùng một lúc |

Các vấn đề về xác suất đã giải quyết
Câu 1: Tìm xác suất để ‘có 3 con lăn trên con súc sắc’.
Giải pháp:
Không gian mẫu = {1, 2, 3, 4, 5, 6}
Số sự kiện thuận lợi = 1
tức là {3}
Tổng số kết quả = 6
Do đó, Xác suất, P = 1/6
Câu 2: Rút ngẫu nhiên một thẻ từ một gói thẻ. Xác suất để quân bài rút ra là quân bài ngửa là bao nhiêu?
Giải pháp:
Một bộ bài tiêu chuẩn có 52 lá.
Tổng số kết quả = 52
Số sự kiện thuận lợi = 4 x 3 = 12 (chỉ được coi là Jack, Queen và King)
Xác suất, P = Số kết quả thuận lợi / Tổng số kết quả = 12/52 = 3/13.
Câu 3: Một bình chứa 4 bi xanh, 5 bi đỏ và 11 bi trắng. Nếu lấy ngẫu nhiên ba quả bóng từ bình, xác suất để quả bóng thứ nhất màu đỏ, quả bóng thứ hai màu xanh và quả bóng thứ ba màu trắng là bao nhiêu?
Lời giải: Xác suất để lấy được bi đầu tiên có màu đỏ hoặc biến cố thứ nhất là 5/20.
Bây giờ, vì chúng ta đã vẽ một quả bóng cho sự kiện đầu tiên xảy ra, nên số khả năng còn lại để sự kiện thứ hai xảy ra là 20 – 1 = 19.
Do đó, xác suất để quả bóng thứ hai có màu xanh hoặc của sự kiện thứ hai là 4/19.
Một lần nữa với sự kiện thứ nhất và thứ hai xảy ra, số khả năng còn lại để sự kiện thứ ba xảy ra là 19 – 1 = 18.
Và xác suất để bi thứ ba có màu trắng hoặc biến cố thứ ba là 18/11.
Do đó, xác suất là 5/20 x 4/19 x 11/18 = 44/1368 = 0,032.
Hoặc chúng ta có thể biểu thị nó là P = 3.2%.
Câu 4: Hai con xúc xắc được tung lên, tìm xác suất để tổng là:
- bằng 1
- bằng 4
- ít hơn 13
Giải pháp:
Xác suất là gì? Cho một ví dụ
Xác suất là một nhánh của toán học liên quan đến sự xuất hiện của một sự kiện ngẫu nhiên. Ví dụ, khi một đồng xu được tung lên không trung, các kết quả có thể xảy ra là Đầu và Đuôi.
Công thức của xác suất là gì?
Công thức xác suất được định nghĩa là khả năng xảy ra một sự kiện bằng tỷ số giữa số kết quả và tổng số kết quả.
Các loại xác suất khác nhau là gì?
Có ba loại xác suất chính:
Xác suất lý thuyết Xác suất
thực nghiệm Xác suất tiên
đề
Các quy tắc cơ bản của xác suất là gì?
Nếu A và B là hai biến cố thì;
P (A ∪ B) = P (A) + P (B) – P (A ∩ B)
P (A ∩ B) = P (B) ⋅ P (A | B)
Xem thêm:
Sự khác biệt giữa lỗi thời gian biên dịch và lỗi thời gian chạy