ng chứa các số hạng trong x và y . Nếu điểm P (x, y) thỏa mãn phương trình của dòng, sau đó điểm P dối trá trên dòng L .
Các dạng phương trình khác nhau của một đường thẳng
- Phương trình của các đường ngang và dọc
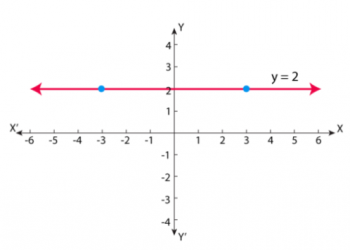
Phương trình của các đường thẳng nằm ngang hoặc song song với trục X là y = a, trong đó a là tọa độ y của các điểm trên đường thẳng.
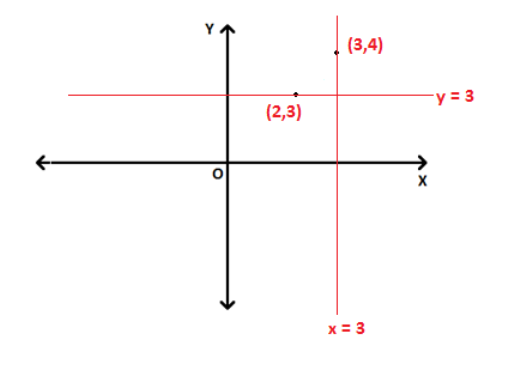
Tương tự, phương trình của một đường thẳng thẳng đứng hoặc song song với trục Y là x = a , trong đó a là tọa độ x của các điểm trên đường thẳng.
Ví dụ, phương trình của đường thẳng song song với trục X và chứa điểm (2,3) là y = 3 .
Tương tự, phương trình của đường thẳng song song với trục Y và chứa điểm (3,4) là x = 3 .
2. Phương trình dạng điểm-độ dốc của đường
Xét một đường thẳng không thẳng đứng L có hệ số góc là m, A (x, y) là một điểm tùy ý trên đường thẳng vàP(x1,y1) là điểm cố định trên cùng một đường thẳng.
Độ dốc của đường theo định nghĩa là,
m = y – y1x – x1
y – y1 = m ( x – x1)
Ví dụ, phương trình của đường thẳng có hệ số góc m = 2 và đi qua điểm ( 2 , 3 ) Là
y – 3 = 2 (x – 2)
y = 2x-4 + 3
2x-y-1 = 0
3. Phương trình dạng hai điểm của đoạn thẳng
Gọi P (x, y) là điểm tổng quát trên đường thẳng L đi qua điểmA (x1,y1) và B (x2,y2).
Vì ba điểm thẳng hàng,
hệ số góc của PA = s lope của AB
y – y1x – x1 = y2 – y1x2 – x1
y–y1= (y2–y1) .x –x1x2–x1
4. Phương trình dạng giao nhau dốc của đường thẳng
Hãy xem xét một đường có hệ số góc là m cái nào cắt đứt Y-axis ở khoảng cách ‘a’ so với gốc tọa độ. Khi đó khoảng cách a được gọi lày– điểm chặn của dòng . Điểm tại đó đường cắty-axis sẽ ( 0 , a ).
Khi đó, phương trình của đường thẳng sẽ là
ya = m (x-0)
y = mx + a
Tương tự, một đường thẳng có hệ số góc m cắt trục X cách gốc tọa độ một khoảng b sẽ tại điểm (b, 0) . Khoảng cách b được gọi là x- giao điểm của đoạn thẳng.
Phương trình của dòng sẽ là:
y = m (xb)
5. Hình thức đánh chặn
Xét đường thẳng L có x – giao điểm a và y – giao điểm b , khi đó đường thẳng tiếp xúc với trục X tại (a, 0) và trục Y tại (0, b).
Theo phương trình dạng hai điểm,
y – 0 = b – 00 – a ( x – a )
y = –ba( x – a )
y = ba( a – x )
xa + yb = 1
Ví dụ, phương trình của đường thẳng có x– đánh chặn 3 và y– đánh chặn 4 Là,
x3 + y4 = 1
4 x + 3 y = 12
6. Hình thức bình thường
Xét một đường vuông góc từ gốc tọa độ có độ dài l đến đường thẳng L và nó tạo một góc β với trục X dương .
Hãy OP là vuông góc với từ nguồn gốc đến dòng L .
Sau đó,
O Q = l c o s β
PQ = Tôi là tôi n β
Tọa độ của điểm P Chúng tôi; P( l c o s β , l s i n β )
độ dốc của con đường O P Là t a n β
Vì thế,
Sl o p e o f t h e l i n e L = –1t a n β = –c o s β s tôi n β
Phương trình của đường thẳng L có độ dốc –c o s β s tôi n β và đi qua điểm ( l c o s β , l s i n β ) Là,
y – l s i n β = –c o s β s tôi n β ( x – l c o s β )
y s i n β – l s i n2 β =– x c o s β + l c o S2 β
x c o s β + y s tôi n β =l ( s in2 β +co S2 β )
x c o s β + y s tôi n β =l
Bạn đã học về các dạng khác nhau của phương trình của một đường thẳng
Xem thêm:
