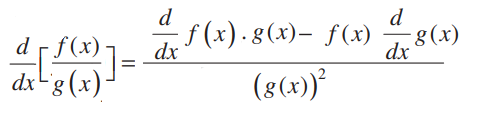
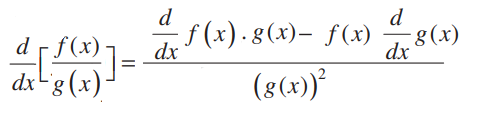
Bây giờ, chúng ta hãy xem định nghĩa của quy tắc thương số trong phân biệt cùng với công thức.Công thức quy tắc thương số
Trong Giải tích, quy tắc Thương số tương tự như quy tắc tích. Quy tắc Thương số được phát biểu bằng tỷ số giữa đại lượng của mẫu số nhân với đạo hàm của hàm số trừ tử số nhân với đạo hàm của hàm số ở mẫu số và bình phương của hàm số mẫu số. Tóm lại, quy tắc quotien t là một cách phân biệt sự phân chia của các hàm hoặc các thương số. Đây còn được gọi là sự phân biệt quy tắc thương số trong toán học .Cho hàm số đã cho là f (x), được cho bởi:[latex] \ large \ mathbf {f (x) = \ frac {s (x)} {t (x)}} [/ latex] ,
Do đó, sự khác biệt của hàm được cho bởi:
[latex] \ large \ mathbf {f ‘(x) = \ left [\ frac {s (x)} {t (x)} \ right]’ = \ frac {t (x) .s ‘(x) – s (x). t ‘(x)} {\ left \ {t (x) \ right \} ^ {2}}} [/ latex]
Các quy tắc thương của sự khác biệt được định nghĩa là tỉ số của hai chức năng (chức năng 1 / Chức năng thứ 2), tương đương với tỷ lệ (Cách phân biệt chức năng 1st [latex] \ lớn \ times [/ latex] chức năng thứ 2 – Cách phân biệt thứ hai function [latex] \ large \ times [/ latex] the first function) thành bình phương của hàm thứ 2.
Ít hơn Biểu tượng là gì? Xem xong 5 phút hiểu luôn.
Contents
Bằng chứng quy tắc thương số
Chúng ta biết, đạo hàm của một hàm số được cho là:
[latex] \ large \ mathbf {f ‘(x) = \ lim \ limit_ {h \ to 0} \ frac {f (x + h) – f (x)} {h}} [/ latex]
Do đó, đạo hàm của tỷ số của hàm là:

Do đó, quy tắc thương số được chứng minh.
Quy tắc thương số Đạo hàm cũng có thể được chứng minh bằng cách sử dụng quy tắc tích và các quy tắc phân biệt khác như được đưa ra dưới đây.
Giả sử hàm f (x) được định nghĩa là tỉ số của hai hàm, giả sử u (x) và v (x), thì đạo hàm của nó có thể được suy ra như giải thích dưới đây.
f (x) = u (x) / v (x)
Điều này cũng có thể được viết là:
f (x) = u (x) [u (x)] -1
Sử dụng quy tắc khác biệt của sản phẩm,
f ‘(x) = u’ (x) [v (x)] -1 + u (x) (d / dx) [v (x)] -1
Chúng ta biết rằng (d / dx) x n = nx n-1 ,
f ‘(x) = u’ (x) [v (x)] -1 + u (x). (- 1) [v (x)] -2 v ‘(x)
= [u ‘(x) / v (x)] – [{u (x) v’ (x)} / {v (x)} 2 ]
= [u ‘(x) v (x) – u (x) v’ (x)] / [v (x)] 2
Đây cũng được gọi là quy tắc thương của u và v.
Do đó, công thức trên có thể được viết là:
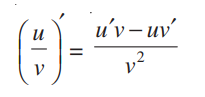
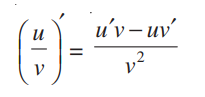
Ví dụ về quy tắc thương số
Hãy để chúng tôi tìm ra một số ví dụ:
Ví dụ 1:
Tìm đạo hàm của [latex] \ tan x [/ latex] .
Giải pháp:
Chúng tôi biết, [latex] \ tan x = \ frac {\ sin x} {\ cos x} [/ latex]
[latex] \ left (\ tan x \ right) ‘= \ frac {\ mathrm {d}} {\ mathrm {d} x} \ left (\ frac {\ sin x} {\ cos x} \ right) [ /mủ cao su]
[latex] = \ left (\ frac {\ cos x. (\ sin x) ‘- \ sin x (\ cos x)’} {\ cos ^ {2} x} \ right) [/ latex]
[latex] = \ left (\ frac {\ cos ^ {2} x + \ sin ^ {2} x} {\ cos ^ {2} x} \ right) [/ latex]
[latex] = \ left (\ frac {1} {\ cos ^ {2} x} \ right) [/ latex] [latex] = \ sec ^ {2} x [/ latex]
Ví dụ 2:
Tìm đạo hàm của [latex] \ sqrt {\ frac {5x + 7} {3x – 2}} [/ latex]
Giải pháp:
[latex] \ sqrt {\ frac {5x + 7} {3x – 2}} = \ frac {\ sqrt {5x + 7}} {\ sqrt {3x – 2}} [/ latex]
Áp dụng quy tắc thương số, chúng ta có
[latex] \ frac {\ mathrm {d}} {\ mathrm {d} x} \ left (\ sqrt {\ frac {5x + 7} {3x – 2}} \ right) = \ frac {\ sqrt {3x – 2}. \ frac {\ mathrm {d}} {\ mathrm {d} x} \ left (\ sqrt {5x + 7} \ right) – \ sqrt {5x + 7}. \ frac {\ mathrm {d}} {\ mathrm {d} x} \ sqrt {3x – 2}} {3x – 2} [/ latex]
[latex] = \ frac {\ sqrt {3x – 2}. \ left (\ frac {5} {2. \ sqrt {5x + 7}} \ right) – \ sqrt {5x + 7}. \ left (\ frac {3} {2. \ sqrt {3x – 2}} \ right)} {3x – 2} [/ latex]
[latex] = \ frac {\ left (\ frac {5. \ sqrt {3x – 2}} {2. \ sqrt {5x + 7}} \ right) – \ left (\ frac {3. \ sqrt {5x + 7}} {2. \ sqrt {3x – 2}} \ right)} {3x – 2} [/ latex]
Lấy LCM, chúng tôi có
[latex] = \ frac {5. \ left (3x – 2 \ right) – 3. \ left (5x + 7 \ right)} {2 \ left (3x – 2 \ right) \ left (\ sqrt {3x – 2} \ right) \ left (\ sqrt {5x + 7} \ right)} [/ latex]
[latex] = \ frac {15x – 10 – 15x – 21} {2 \ left (3x – 2 \ right) ^ {\ frac {3} {2}} \ left (5x + 7 \ right) ^ {\ frac {1} {2}}} [/ latex]
[latex] = \ frac {-31} {2 \ left (3x – 2 \ right) ^ {\ frac {3} {2}} \ left (5x + 7 \ right) ^ {\ frac {1} {2 }}}[/mủ cao su]
Ví dụ 3:
Tìm đạo hàm của [latex] \ frac {(x + 3) ^ {4}} {\ sqrt {x ^ {2} +5}} [/ latex]
Giải pháp:
Áp dụng quy tắc thương số, chúng ta có
[latex] \ frac {\ mathrm {d}} {\ mathrm {d} x} \ left (\ frac {(x + 3) ^ {4}} {\ sqrt {x ^ {2} +5}} \ right) = \ frac {\ sqrt {x ^ {2} +5}. \ frac {\ mathrm {d}} {\ mathrm {d} x} (x + 3) ^ {4} – (x + 3) ^ {4}. \ frac {\ mathrm {d}} {\ mathrm {d} x} \ left (\ sqrt {x ^ {2} +5} \ right)} {x ^ {2} +5} [/ latex]
[latex] = \ frac {\ sqrt {x ^ {2} +5} .4 (x + 3) ^ {3} – (x + 3) ^ {4}. \ frac {2x} {2 \ sqrt {x ^ {2} +5}}} {x ^ {2} +5} [/ latex]
[latex] = \ frac {4. \ left (x ^ {2} +5 \ right). (x + 3) ^ {3} – x. (x + 3) ^ {4}} {\ left (x ^ {2} +5 \ right) ^ {\ frac {3} {2}}} [/ latex]
[latex] = \ frac {\ left (x + 3 \ right) ^ {3} \ left [4. \ left (x ^ {2} +5 \ right) – x. (x + 3) \ right]} {\ left (x ^ {2} +5 \ right) ^ {\ frac {3} {2}}} [/ latex]
[latex] = \ frac {\ left (x + 3 \ right) ^ {3} \ left [4x ^ {2} + 20 – x ^ {2} – 3x \ right]} {\ left (x ^ {2 } +5 \ right) ^ {\ frac {3} {2}}} [/ latex]
[latex] = \ frac {\ left (x + 3 \ right) ^ {3} \ left [3x ^ {2} -3x + 20 \ right]} {\ left (x ^ {2} +5 \ right) ^ {\ frac {3} {2}}} [/ latex]
Vấn đề thực hành
Thực hành các câu hỏi dưới đây để hiểu quy tắc thương một cách hiệu quả.
- Tìm đạo hàm của f (x) = (x + 2) / (3x).
- Tìm đạo hàm của hàm số f (x) = (2x + 3) / (x – 3).
- Tìm công thức tính đạo hàm của cot x bằng quy tắc thương.
- Tìm đạo hàm của f (x) = (x + cos x) / tan x
Câu hỏi thường gặp – Câu hỏi thường gặp
Làm thế nào để bạn sử dụng quy tắc thương số để phân biệt?
Quy tắc thương trong toán học là gì?
Làm thế nào để bạn tìm thấy đạo hàm của một hàm chia?
Công thức của quy tắc Thương số là gì?
f ‘(x) = [u’ (x) v (x) – u (x) v ‘( x)] / [v (x)] ^ 2
Đạo hàm của (x – 1) / 2x là gì?
Bây giờ, theo quy tắc thương, đạo hàm của hàm đã cho trở thành,
(d / dx) [u (x) / v (x)] = [u ‘(x) v (x) – u (x) v’ (x )] / [v (x)] ^ 2
= [1 (2x) – (x – 1) (2)] / (2x) ^ 2
= (2x – 2x + 1) / 4x ^ 2
= 1 / 4x ^ 2