Annulus là gì ? Cùng tìm hiểu về nó.

Annulus

Hình khuyên là một hình được tạo bởi hai hình tròn. Nó là một hình máy bay được tạo thành bởi hai vòng tròn đồng tâm. Vùng được bao phủ giữa hai vòng tròn đồng tâm được gọi là hình vành khuyên. Nó có dạng hình chiếc nhẫn và có nhiều ứng dụng trong Toán học. Một số ví dụ trong cuộc sống thực là ngón tay đeo nhẫn, hạt bột, v.v. Diện tích của hình khuyên được xác định nếu chúng ta biết diện tích của các hình tròn (cả bên trong và bên ngoài). Công thức để tìm hình khuyên của đường tròn được cho bởi:

A = π (R ² -r ² )

trong đó ‘R’ là bán kính của đường tròn ngoại tiếp và ‘r’ là bán kính của đường tròn bên trong. Ở đây, chúng ta sẽ tìm hiểu ý nghĩa hoàn chỉnh và khu vực của nó cùng với các ví dụ.

Đường tròn là một khái niệm nền tảng không chỉ trong Toán học mà còn trong nhiều lĩnh vực. Theo định nghĩa của nó, chúng ta biết, một đường tròn là một hình phẳng được tạo thành từ các điểm nằm ở cùng một khoảng cách từ một điểm cụ thể. Xem một hình của một hình tròn được cho ở đây.

Nó cho thấy một vòng tròn hoàn chỉnh với một số bán kính. Bây giờ nếu cùng một vòng tròn được bao quanh bởi một vòng tròn khác với khoảng trống ở giữa chúng và bán kính lớn hơn vòng tròn này, thì vùng được tạo thành ở giữa hai vòng tròn về cơ bản là hình khuyên. Hãy cùng chúng tôi tìm hiểu ý nghĩa của nó về mặt hình học cùng với công thức diện tích và các ví dụ đã giải dựa trên nó.

Annulus Ý nghĩa

Từ “ annulus ” (số nhiều – annuli) có nguồn gốc từ tiếng Latinh, có nghĩa là “ chiếc nhẫn nhỏ ”. Hình khuyên được gọi là diện tích giữa hai đường tròn đồng tâm (các đường tròn có tâm trùng với nhau) nằm trong cùng một mặt phẳng.

Nó là vùng giới hạn giữa hai vòng tròn có chung tâm. Hình dạng này giống như một chiếc nhẫn phẳng. Nó cũng có thể được coi là một đĩa tròn có một lỗ tròn ở giữa. Xem hình ở đây cho thấy một hình khuyên.

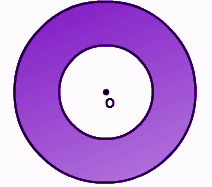
Ở đây, có thể nhìn thấy hai vòng tròn, trong đó một vòng tròn nhỏ nằm bên trong vòng tròn lớn hơn. Điểm O là tâm của cả hai đường tròn. Vùng được tô màu, nằm giữa ranh giới của hai vòng tròn này, được gọi là hình khuyên. Vòng tròn nhỏ hơn được gọi là vòng tròn bên trong, trong khi vòng tròn lớn hơn được gọi là vòng tròn bên ngoài.

Nói cách khác, bất kỳ vật thể hình nhẫn phẳng hai chiều nào được tạo thành bởi hai vòng tròn đồng tâm được gọi là hình khuyên.

Khu vực Annulus

Diện tích của hình khuyên có thể được tính bằng cách tìm diện tích của hình tròn bên ngoài và hình tròn bên trong. Sau đó, chúng ta phải trừ diện tích của cả hai hình tròn để có được kết quả. Chúng ta hãy xem xét một con số:

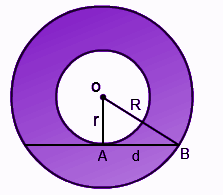
Trong hình trên, hai đường tròn có chung tâm O. Gọi bán kính đường tròn ngoại tiếp là “R” và bán kính đường tròn nội tiếp là “r”. Phần bóng mờ biểu thị một hình khuyên. Để tìm diện tích của hình khuyên này, chúng ta bắt buộc phải tìm diện tích của các hình tròn.

Vì thế,

Diện tích hình tròn ngoài = πR ²

Diện tích của vòng tròn bên trong = πr ²

Area of ​​Annulus = Area of ​​Outer Circle – Diện tích của vòng tròn bên trong

Vì thế,

Hoặc chúng ta cũng có thể viết nó là;

Ví dụ về Annulus

H.1: Tính diện tích của một hình khuyên có bán kính ngoài là 14 cm và bán kính trong là 7 cm?

Giải: Cho biết bán kính ngoài R = 14 cm và bán kính trong r = 7 cm

Diện tích hình tròn bên ngoài = πR ² = 22/7 x 14 x 14

= 22 x 14 x 2

= 616 cm ²

Diện tích hình tròn bên trong = πr ² = 22/7 x 7 x 7

= 22 x 7

= 154 cm ²

Diện tích hình khuyên = Diện tích hình tròn bên ngoài – Diện tích hình tròn bên trong

Diện tích hình khuyên = 616 – 154

Diện tích hình khuyên = 462 cm ²

Q.2: Nếu diện tích của một hình khuyên là 1092 inch và chiều rộng của nó là 3 cm, thì hãy tìm bán kính của hình tròn trong và ngoài.

Giải: Cho bán kính trong của một hình tròn là r và bán kính ngoài của nó là R.

Khi đó chiều rộng = R – r

3 = R – r

R = 3 + r

Chúng tôi biết,

Diện tích hình khuyên = π (R ² −r ² )

hoặc là

Diện tích hình khuyên = π (R + r) (R – r)

1092 = 22/7 (3 + r + r) (3)

3 + 2r = 1092 × 722 × 3

3 + 2r = 115,82

2r = 115,82 – 3

2r = 112,82

r = 56,41

R = 3 + 56,41

= 59,41

Vì vậy, bán kính bên trong = 56,41 inch

Bán kính bên ngoài = 59,41 inch

Xem thêm: