Đa thức là gì? Xem xong 5 phút hiểu luôn.

Đa thức là biểu thức đại số bao gồm các biến và hệ số. Các biến đôi khi còn được gọi là giá trị không xác định. Chúng ta có thể thực hiện các phép tính số học như cộng, trừ, nhân và cả số mũ nguyên dương đối với biểu thức đa thức nhưng không chia cho biến. Ví dụ về đa thức với một biến là x ² + x-12. Trong ví dụ này, có ba số hạng: x ² , x và -12.

Từ polynomial có nguồn gốc từ tiếng Hy Lạp ‘poly’ có nghĩa là ‘ nhiều ‘ và ‘danh nghĩa’ có nghĩa là ‘ điều khoản ‘, vì vậy nhìn chung nó được gọi là “nhiều điều khoản”. Một đa thức có thể có bất kỳ số hạng nào nhưng không phải là vô hạn. Tìm hiểu về bậc, số hạng, kiểu, tính chất, hàm đa thức trong bài viết này.

Đa thức là gì?

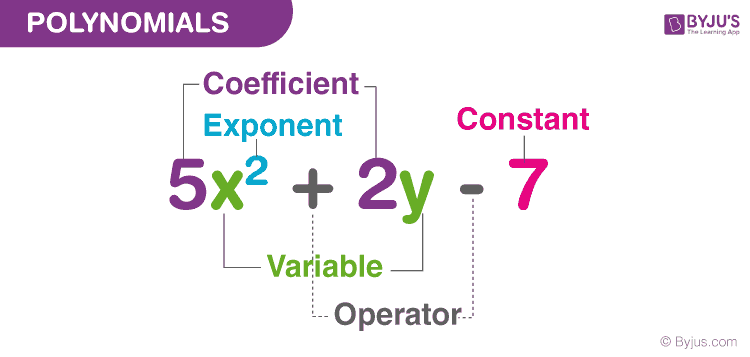
Đa thức được tạo thành từ hai thuật ngữ, đó là Poly (nghĩa là “nhiều”) và Nominal (nghĩa là “số hạng”). Đa thức được định nghĩa là một biểu thức bao gồm các biến, hằng số và số mũ, được kết hợp bằng cách sử dụng các phép toán như cộng, trừ, nhân và chia (Không có phép toán chia cho một biến). Dựa vào số hạng có trong biểu thức, nó được phân loại thành đơn thức, nhị thức và tam thức. Ví dụ về hằng số, biến và số mũ như sau:

• Các hằng số. Ví dụ: 1, 2, 3, v.v.
• Biến. Ví dụ: g, h, x, y, v.v.
• Số mũ: Ví dụ: 5 in x ^5, v.v.

Ký hiệu

Hàm đa thức được ký hiệu là P (x) trong đó x là biến số. Ví dụ,

P (x) = x ² -5x + 11

Nếu biến được ký hiệu là a, thì hàm sẽ là P (a)

Mức độ của một đa thức

Các mức độ của một đa thức được định nghĩa là mức độ cao nhất của một đơn thức trong vòng một đa thức. Do đó, một phương trình đa thức có một biến có số mũ lớn nhất được gọi là bậc của đa thức.

Ví dụ: Tìm bậc của đa thức 6s ⁴ + 3x ² + 5x +19

Giải pháp:

Bậc của đa thức là 4.

Thuật ngữ của một đa thức

Các số hạng của đa thức là các phần của phương trình thường được phân tách bằng dấu “+” hoặc “-”. Vì vậy, mỗi phần của một đa thức trong một phương trình là một số hạng. Ví dụ, trong một đa thức, giả sử, 2x ² + 5 +4, số hạng tử sẽ là 3. Việc phân loại một đa thức được thực hiện dựa trên số hạng tử trong đó.

Các loại đa thức

Đa thức có 3 loại khác nhau và được phân loại dựa trên số hạng tử trong đó. Ba loại đa thức là:

• Đơn thức
• Nhị thức
• Tam thức

Các đa thức này có thể được kết hợp bằng cách sử dụng cộng, trừ, nhân và chia nhưng không bao giờ chia cho một biến. Một vài ví dụ về Đa thức không là: 1 / x + 2, x ^-3

Đơn thức

Đơn thức là một biểu thức chỉ chứa một số hạng. Đối với một biểu thức là một đơn thức, số hạng đơn phải là một số hạng khác không. Một vài ví dụ về đơn thức là:

• 5x
• 3
• 6a ⁴
• -3xy

Nhị thức

Nhị thức là một biểu thức đa thức chứa đúng hai số hạng. Một nhị thức có thể được coi là một tổng hoặc hiệu giữa hai hoặc nhiều đơn thức. Một vài ví dụ về nhị thức là:

• – 5x + 3,
• 6a ⁴ + 17x
• xy ² + xy

Tam thức

Một tam thức là một biểu thức bao gồm đúng ba số hạng. Một vài ví dụ về biểu thức tam thức là:

• – 8a ⁴ + 2x + 7
• 4x ² + 9x + 7

Tính chất

Một số tính chất quan trọng của đa thức cùng với một số định lý về đa thức quan trọng như sau:

Thuộc tính 1: Thuật toán phân chia

Nếu một đa thức P (x) chia cho một đa thức G (x) được kết quả là thương Q (x) với phần dư R (x), thì,

P (x) = G (x) • Q (x) + R (x)

Tính chất 2: Định lý Bezout

Đa thức P (x) chia hết cho nhị thức (x – a) nếu và chỉ khi P (a) = 0 .

Tính chất 3: Định lý phần dư

Nếu P (x) chia cho (x – a) có dư r thì P (a) = r .

Tính chất 4: Định lý thừa số

Một đa thức P (x) chia cho Q (x) được kết quả là R (x) không có dư nếu và chỉ khi Q (x) là một thừa số của P (x).

Tính chất 5: Định lý Giá trị Trung bình

Nếu P (x) là một đa thức và P (x) ≠ P (y) với (x <y), thì P (x) nhận mọi giá trị từ P (x) đến P (y) trong khoảng đóng [x , y].

Thuộc tính 6

Phép cộng, trừ và nhân các đa thức P và Q dẫn đến một đa thức trong đó,

Độ (P ± Q) ≤ Độ (P hoặc Q)

Bằng (P × Q) = Bằng (P) + Bằng (Q)

Thuộc tính 7

Nếu một đa thức P chia hết cho một đa thức Q thì mọi số 0 của Q cũng bằng 0 của P.

Tài sản 8

Nếu một đa thức P chia hết cho hai đa thức Q và R thì nó chia hết cho (Q • R).

Thuộc tính 9

Nếu P (x) = a ₀ + a ₁ x + a ₂ x ² + …… + a _n x ⁿ là đa thức sao cho deg (P) = n ≥ 0 thì P có nhiều nhất “n” nghiệm phân biệt.

Thuộc tính 10: Quy tắc ký hiệu của Descartes

Số lượng các số 0 thực dương trong một hàm đa thức P (x) bằng hoặc nhỏ hơn một số chẵn như số lần thay đổi dấu của các hệ số. Vì vậy, nếu có thay đổi dấu “K”, số gốc sẽ là “k” hoặc “(k – a)”, trong đó “a” là một số chẵn.

Tính chất 11: Định lý cơ bản của Đại số

Mọi đa thức đơn biến không hằng số với hệ số phức đều có ít nhất một căn phức.

Tài sản 12

Nếu P (x) là một đa thức với hệ số thực và có một số phức 0 (x = a – bi), thì x = a + bi cũng sẽ là một số không của P (x). Ngoài ra, x ² – 2ax + a ² + b ² sẽ là một thừa số của P (x).

Phương trình đa thức

Phương trình đa thức là những biểu thức được tạo thành từ nhiều hằng và biến. Hình thức tiêu chuẩn của việc viết một phương trình đa thức là đặt bậc cao nhất trước rồi cuối cùng là số hạng không đổi. Một ví dụ về phương trình đa thức là:

b = a ⁴ + 3a ³ -2a ² + a +1

Hàm đa thức

Một hàm đa thức là một biểu thức được xây dựng với một hoặc nhiều số hạng của biến với số mũ không đổi. Nếu có các số thực được ký hiệu là a thì hàm có một biến và bậc n có thể được viết là:

Giải đa thức

Bất kỳ đa thức nào có thể được giải quyết dễ dàng bằng cách sử dụng các khái niệm đại số và thừa số cơ bản. Trong khi giải phương trình đa thức, bước đầu tiên là đặt vế phải là 0. Lời giải của một nghiệm đa thức được giải thích theo hai cách khác nhau:

• Giải các đa thức tuyến tính
• Giải đa thức bậc hai

Giải các đa thức tuyến tính

Nhận nghiệm của đa thức tuyến tính rất dễ dàng và đơn giản. Đầu tiên, cô lập số hạng biến và làm cho phương trình bằng 0. Sau đó giải quyết như hoạt động đại số cơ bản. Dưới đây là một ví dụ về việc tìm nghiệm của một phương trình tuyến tính:

Ví dụ: Giải 3x – 9

Giải pháp:

Đầu tiên, lập phương trình dưới dạng 0. Vì vậy,

3x – 9 = 0

⇒ 3x = 9

⇒ x = 9/3

Hoặc, x = 3.

Như vậy, nghiệm của 3x-9 là x = 3.

Giải đa thức bậc hai

Để giải một đa thức bậc hai, trước tiên, hãy viết lại biểu thức theo thứ tự bậc giảm dần. Sau đó, quy về phương trình và thực hiện nhân thừa đa thức để nhận được nghiệm của phương trình. Dưới đây là một ví dụ để tìm nghiệm của một đa thức bậc hai được đưa ra dưới đây để hiểu rõ hơn.

Ví dụ: Giải 3x ² – 6x + x ³ – 18

Giải pháp:

Đầu tiên, sắp xếp đa thức theo thứ tự giảm dần của bậc và bằng không.

⇒ x ³ + 3x ² -6x – 18 = 0

Bây giờ, hãy sử dụng các thuật ngữ chung.

x ² (x + 3) – 6 (x + 3) = 0

⇒ (x ² -6) (x + 3) = 0

Vì vậy, các nghiệm sẽ là x = -3 và

x ² = 6

Hoặc, x = √6

Phép toán đa thức

Có bốn phép toán đa thức chính là:

• Phép cộng các đa thức
• Phép trừ các đa thức
• Nhân các đa thức
• Phân chia đa thức

Mỗi phép toán trên đa thức được giải thích dưới đây bằng cách sử dụng các ví dụ đã giải.

Phép cộng các đa thức

Để thêm đa thức, hãy luôn thêm các số hạng tương tự, tức là các số hạng có cùng biến và lũy thừa. Phép cộng các đa thức luôn tạo ra một đa thức cùng bậc. Ví dụ,

Ví dụ: Tìm tổng của hai đa thức: 5x ³ + 3x ² y + 4xy − 6y ² , 3x ² + 7x ² y − 2xy + 4xy ² −5

Giải pháp:

Đầu tiên, hãy kết hợp các cụm từ tương tự trong khi vẫn giữ nguyên các cụm từ không giống như chúng. Vì thế,

(5x ³ + 3x ² y + 4xy − 6y ² ) + (3x ² + 7x ² y − 2xy + 4xy ² −5)

= 5x ³ + 3x ² + (3 + 7) x ² y + (4−2) xy + 4xy ² −6y ² −5

= 5x ³ + 3x ² + 10x ² y + 2xy + 4xy ² −6y ² −5

Phép trừ các đa thức

Phép trừ đa thức cũng tương tự như phép cộng, điểm khác biệt duy nhất là kiểu hoạt động. Vì vậy, trừ các số hạng tương tự để có được giải pháp. Cần lưu ý rằng phép trừ các đa thức cũng cho kết quả là một đa thức có cùng bậc.

Ví dụ: Tìm hiệu của hai đa thức: 5x ³ + 3x ² y + 4xy − 6y ² , 3x ² + 7x ² y − 2xy + 4xy ² −5

Giải pháp:

Đầu tiên, hãy kết hợp các cụm từ tương tự trong khi vẫn giữ nguyên các cụm từ không giống như chúng. Vì thế,

(5x ³ + 3x ² y + 4xy − 6y ² ) – (3x ² + 7x ² y − 2xy + 4xy ² −5)

= 5x ³ -3x ² + (3-7) x ² y + (4 + 2) xy-4xy ² −6y ² +5

= 5x ³ -3x ² -4x ² y + 6xy-4xy ² -6y ² 5

Nhân các đa thức

Hai hoặc nhiều đa thức khi nhân lên luôn tạo ra đa thức có bậc cao hơn (trừ khi một trong số chúng là đa thức hằng số). Dưới đây là một ví dụ về nhân đa thức :

Ví dụ: Giải (6x − 3y) × (2x + 5y)

Giải pháp:

⇒ 6x × (2x + 5y) –3y × (2x + 5y) ———- Sử dụng luật phân phối của phép nhân

⇒ (12x ² + 30xy) – (6yx + 15y ² ) ———- Sử dụng luật phân phối của phép nhân

⇒12x ² + 30xy – 6xy – 15y ² —————– như xy = yx

Do đó, (6x − 3y) × (2x + 5y) = 12x ² + 24xy − 15y ²

Phân chia đa thức

Phép chia hai đa thức có thể tạo ra một đa thức hoặc không. Hãy cùng chúng tôi nghiên cứu chi tiết dưới đây về phép chia các đa thức. Để chia đa thức, hãy làm theo các bước đã cho:

Các bước phân chia đa thức:

Nếu một đa thức có nhiều hơn một số hạng, chúng ta sử dụng phương pháp chia dài cho cùng một số hạng. Sau đây là các bước cho nó.

1. Viết đa thức theo thứ tự giảm dần.
2. Kiểm tra quyền lực cao nhất và chia các số hạng cho cùng.
3. Sử dụng câu trả lời ở bước 2 làm biểu tượng chia.
4. Bây giờ hãy trừ nó đi và đưa ra số hạng tiếp theo.
5. Lặp lại bước 2 đến bước 4 cho đến khi bạn không còn điều khoản nào nữa.
6. Lưu ý rằng câu trả lời cuối cùng, bao gồm cả phần dư, sẽ ở dạng phân số (số hạng trừ cuối cùng).

Ví dụ về đa thức

Thí dụ:

Cho hai đa thức 7s ³ + 2s ² + 3s + 9 và 5s ² + 2s + 1.

Giải quyết những điều này bằng cách sử dụng phép toán.

Giải pháp:

Đa thức đã cho:

7s ³ + 2s ² + 3s + 9 và 5s ² + 2s + 1

Phép cộng đa thức: (7s ³ + 2s ² + 3s + 9) + (5s ² + 2s + 1)

= 7 giây ³ + (2 giây ² + 5 giây ² ) + (3 giây + 2 giây) + (9 + 1)

= 7 giây ³ + 7 giây ² + 5s + 10

Do đó, phép cộng dẫn đến một đa thức.

Phép trừ đa thức: (7s ³ + 2s ² + 3s + 9) – (5s ² + 2s + 1)

= 7s ³ + (2s ² -5s ² ) + (3s-2s) + (9-1)

= 7s ³ -3s ² + s + 8

Do đó, phép cộng dẫn đến một đa thức.

Phép nhân đa thức: (7s ³ + 2s ² + 3s + 9) × (5s ² + 2s + 1)

= 7s ³ (5s ² + 2s + 1) + 2s ² (5s ² + 2s + 1) + 3s (5s ² + 2s + 1) +9 (5s ² + 2s + 1))

= (35 giây ⁵ + 14 giây ⁴ + 7 giây ³ ) + (10 giây ⁴ + ⁴ giây ³ + 2 giây ² ) + (15 giây ³ + 6 giây ² + 3 giây ) + (45 giây ² + 18 giây + 9)

= 35 ⁵ + (14s ⁴ + 10s ⁴ ) + (7s ³ + 4s ³ + 15s ³ ) + (2s ² + 6s ² + 45s ² ) + (3s + 18s) 9

= 35 giây ⁵ + 24 giây ⁴ + 26 giây ³ + 53 giây ² + 21 giây +9

Phép chia đa thức: ( 7s ³ + 2s ² + 3s + 9) ÷ (5s ² + 2s + 1)

(7 giây ³ + 2 giây ² + 3 giây + 9) / (5 giây ² + 2 giây + 1)

Điều này không thể được đơn giản hóa. Do đó, phép chia các đa thức này không tạo ra một Đa thức.