Công thức mặt cầu dành cho những người yêu Toán

Bạn đang tìm hiểu những kiến thức liên quan đến mặt cầu và các công thức mặt cầu, thể tích mặt cầu…Đây là một dạng bài tập quan trọng, kiến thức trọng tâm của toán học lớp 12, do đó các bạn cần nắm chắc và tổng hợp đầy đủ để không bỏ sót các công thức này.

Hôm nay để giúp các bạn có thể dễ dàng tổng hợp và hệ thống lại các kiến thức liên quan đến mặt cầu, tintuctuyensinh của chúng tôi sẽ giúp bạn củng cố lại kiến thức liên quan đến vấn đề này.

1. Nhận thức chung về công thức mặt cầu

Trong cuộc sống hàng ngày chúng ta có thể thấy có rất nhiều các đồ vật có dạng hình cầu như quả bóng chuyền, bóng đá, bóng rổ, viên bi, hay trái đất của chúng ta là các vật thể có hình dạng hình cầu.

Vậy khái niệm mặt cầu là gì và các dạng bài tập liên quan đến diện tích và thể tích của mặt cầu được tính bằng công thức gì?

Trong hệ trục tọa không gian Oxyz ba chiều, khái niệm mặt cầu được định nghĩa là quỹ tích những điểm cách đều một điểm cho trước O cố định một khoảng không đổi R thì gọi là mặt cầu tâm O.

Điểm O được gọi là tâm và khoảng cách từ O tới một điểm bất kỳ trên mặt cầu là R hay gọi là bán kính của mặt cầu.

Mặt cầu còn được hiểu là một hình cầu 3 chiều

Phân biệt khái niệm mặt cầu và khối cầu:

Khối cầu hay còn gọi là hình cầu là tập hợp các điểm nằm bên trong không gian của mặt cầu.

Phân biệt đơn giản mặt cầu là phần bên ngoài còn khối cầu là toàn bộ phần bên ngoài và không gian bên trong.

2. Các công thức mặt cầu, hình cầu liên quan

Công thức hình cầu, mặt cầu:

S = 4πr2 = πd2

Trong đó:

S là diện tích mặt cầu

r là bán kính mặt cầu/hình cầu

d là đường kính mặt cầu/hình cầu

Công thức tính thể tích mặt cầu, hình cầu:

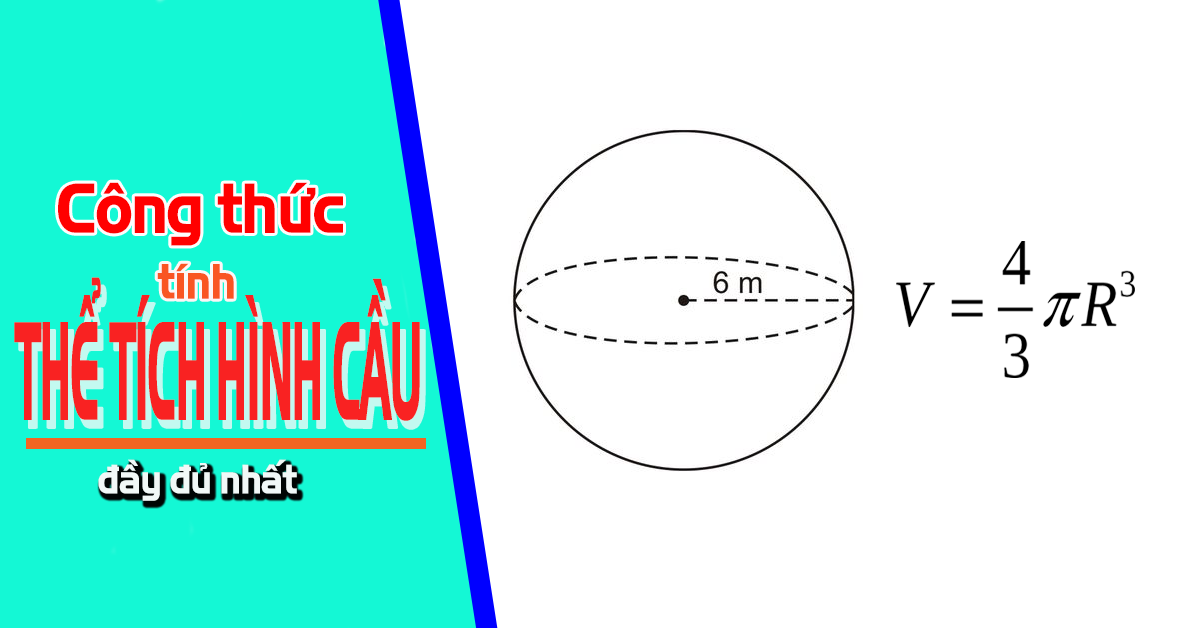
V = 4/3. πr3

Trong đó

V là thể tích hình cầu

r là bán kính mặt cầu/hình cầu

Hai công thức trên tuy ngắn gọn nhưng để nhớ lâu dài và áp dụng thành thạo thì cũng khá khó bởi lượng kiến thức toán học tương đối nhiều do đó nhớ đúng để vận dụng là một vấn đề qua trọng.

Ví dụ:

Cho hình cầu tâm O bán kính r trong đó bán kính r bằng 6cm. Hỏi diện tích của mặt cầu này là bao nhiêu?

Giải:

 Áp dụng công thức tính diện tích mặt cầu ta có:

S = 4πr2 = 4π62 = 144π cm2

Vậy kết quả diện tích mặt cầu đã cho là 144π cm2

Ví dụ bài toán liên quan đến tính thể tích mặt cầu

Cho một mặt cầu tâm O bán kính r trong đó r dài 3 cm. Hỏi thể tích của mặt cầu là bao nhiêu?

Giải: 

Áp dụng công thức tính thể tích mặt cầu ta có

V = 4/3 π r3 = 4/3 π 33 = 36 cm3

Xem thêm:

Phân số tương đương và những cách giải nhanh chóng nhất

Các loại hình tam giác và tất tần tật thông tin về nó

Quy tắc Cosine và những cách giải hay nhất hiện nay

3. Các phương trình liên quan đến mặt cầu

Trong hệ trục tọa độ Oxyz, Cho mặt cầu tâm I( a;b;c) bán kính R > 0

Khi đó ta có:

Phương trình chính tắc của mặt cầu là

( X – a)2 + ( Y – b)2 + ( Z – c)2 = R2

Phương trình tổng quát của mặt cầu là 

X2 + Y2 + Z2 – 2ax – 2by – 2cz + d = 0

Trong đó điều kiện để phương trình tồn tại là a2  + b2 + c2 – d >0

Bán kính R =√(a2  + b2 + c2 – d)

Ví dụ bài tập liên quan đến phương trình mặt cầu:

Trong không gian Oxyz, mặt cầu (S): x²+y²+z²-8x+8y-4z=0 có tâm và bán kính lần lượt là:

4. I(-2;2;-1), R=4.
5. I(4;-4;2), R=6
6. I(-4;4;2), R=6.
7. I(2;-2;1), R=4.

Lời giải và Hướng dẫn:

Đầu tiên ta cần kiểm tra hệ số của x², y², z² nếu khác 1 thì cần chia cả 2 vế cho số phù hợp để trở thành dạng tổng quát. Ở bài này do có hệ số là 1 do đó chúng ta giữ nguyên 

Tiếp theo để xác định tọa độ tâm mặt cầu chúng ta lấy hệ số của x, y, z chia cho -2 ta được: I(4;-4;2).

Để xác định bán kính mặt cầu ta áp dụng công thức tính tổng bình phương các tọa độ của tâm trừ hệ số tự do được kết quả bao nhiêu thì lấy căn bậc 2.

Bán kính mặt cầu là 

R²=4²+(-4)²+2²-0=36⇒R=6. 

Vậy đáp án đúng là đáp án B.

Như vậy các công thức mặt cầu và cách tính diện tích mặt cầu và thể tích hình cầu, mặt cầu được sử dụng khá phổ biến trong các bài toán hình học trong chương trình trung học phổ thông phổ biến. Đặc biệt các công thức tính diện tích, thể tích hình cầu, mặt cầu có mối quan hệ mật thiết với công thức tính thể tích hình lập phương, hình trụ hoặc hình hộp chữ nhật.

Trên đây là toàn bộ những công thức mặt cầu và phương trình liên quan đến mặt cầu, hình cầu mà tintuctuyensinh của chúng tôi cung cấp cho bạn. Hy vọng đây là có sở cho bạn hệ thống lại kiến thức toán học của mình để có phương pháp học tập và nghiên cứu khoa học nhất.

Chúc các bạn thành công!!!