Cách tính diện tích bề mặt của hình nón đơn giản nhất

Diện tích bề mặt của hình nón – Giải thích & Ví dụ

Hình nón là một hình quan trọng khác trong hình học. Để nhớ lại, một hình nón là một cấu trúc ba chiều có đáy là hình tròn, nơi tập hợp các đoạn thẳng, nối tất cả các điểm trên mặt đáy với một điểm chung gọi là khối chóp. Nó được hiển thị trong hình bên dưới.

Khoảng cách thẳng đứng từ tâm đến đỉnh của một hình nón là chiều cao (h) trong khi chiều cao nghiêng của hình nón là chiều dài (l).

Diện tích bề mặt của hình nón là tổng diện tích của mặt cong nghiêng và diện tích của đáy hình tròn.

Trong bài này, chúng ta sẽ thảo luận về cách tìm diện tích bề mặt của một hình nón bằng cách sử dụng diện tích bề mặt của một công thức hình nón . Chúng ta cũng sẽ thảo luận về diện tích bề mặt bên của một hình nón.

Làm thế nào để tìm diện tích bề mặt của một hình nón?

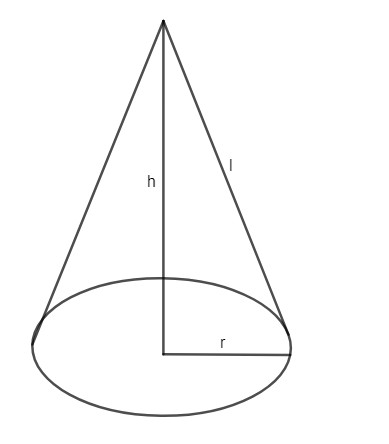
Để tìm diện tích bề mặt của một hình nón, bạn cần tính diện tích đáy của hình nón và diện tích mặt bên.

Vì đáy của hình nón là hình tròn nên diện tích đáy (B) của hình nón là:

Diện tích cơ sở của hình nón, B = πr²

Trong đó  r  = bán kính cơ sở của hình nón

Diện tích bề mặt bên của hình nón

Mặt cong của hình nón có thể được xem như một tam giác có độ dài đáy bằng 2 πr (chu vi hình tròn) và chiều cao bằng chiều cao nghiêng ( l ) của hình nón.

Vì chúng ta biết, diện tích tam giác = ½ bh

Do đó, diện tích mặt bên của hình nón được cho là:

Diện tích bề mặt bên = 1/2 × l × 2πr

Bằng cách đơn giản hóa phương trình, chúng tôi nhận được,

Diện tích bề mặt bên của hình nón, (LSA) = πrl

Diện tích bề mặt của một công thức hình nón

Tổng diện tích bề mặt của hình nón = Diện tích đáy + diện tích bề mặt bên. Do đó, công thức cho tổng diện tích bề mặt của một hình nón được biểu diễn như sau:

Tổng diện tích bề mặt của hình nón = πr ² + πrl

Bằng cách lấy πr làm thừa số chung từ RHS, chúng ta nhận được;

Tổng diện tích bề mặt của một hình nón = πr (l + r) ………………… (Diện tích bề mặt của một hình nón)

Trong đó r = bán kính của đế và l = chiều cao nghiêng

Theo Định lý Pitago, chiều cao nghiêng, l = √ (h ² + r ² )

Các ví dụ đã giải quyết

ví dụ 1

Bán kính và chiều cao của hình nón lần lượt là 9 cm và 15 cm. Tìm diện tích toàn phần của hình nón.

Giải pháp

Được:

Bán kính, r = 9 cm

Chiều cao, h = 15 cm

Chiều cao nghiêng, l = √ (h ² + r ² )

l = √ (15 ² + 9 ² )

= √ (225 + 81)

= √306

= 17,5

Như vậy, chiều cao nghiêng, l = 17,5 cm

Bây giờ thay các giá trị vào diện tích bề mặt của một công thức hình nón

TSA = πr (l + r)

= 3,14 x 9 (9 + 17,5)

= 28,26 x 157,5

= 4.450,95 cm ²

Ví dụ 2

Tính diện tích mặt bên của hình nón có bán kính 5 m và chiều cao nghiêng là 20 m.

Giải pháp

Được;

Bán kính, r = 5 m

Chiều cao nghiêng, l = 20 m

Nhưng, diện tích bề mặt bên của hình nón = πrl

= 3,14 x 5 x 20

= 314 m ²

Ví dụ 3

Tổng diện tích bề mặt của một hình nón là 83,2 ft ² . Nếu chiều cao nghiêng của hình nón là 5,83 ft, hãy tìm bán kính của hình nón.

Giải pháp

Được;

TSA = 83,2 ft ²

Chiều cao nghiêng, l = 5 .83ft

Nhưng, TSA = πr (l + r)

83,2 = 3,14 xr (5,83 + r)

83,2 = 3,14 xr (5,83 + r)

Bằng cách áp dụng thuộc tính phân phối của phép nhân trên RHS, chúng ta nhận được

83,2 = 18,3062r + 2,14r ²

Chia mỗi số hạng cho 3,14

26,5 = 3,14r + r ²

r ² + 3,14r – 26,5 = 0

r = 3,8

Do đó, bán kính của hình nón là 3,8 ft

Ví dụ 4

Tổng diện tích bề mặt của một hình nón là 625 trong ² . Nếu chiều cao nghiêng gấp ba lần bán kính của hình nón, hãy tìm kích thước của hình nón.

Giải pháp

Được;

TSA = 625 trong ²

Chiều cao nghiêng = 3 x bán kính của hình nón

Gọi bán kính của hình nón là x

Chiều cao nghiêng = 3x

TSA = πr (l + r)

625 = 3,14x (3x + x)

Chia cả hai vế cho 3,14.

199,04 = x (4x)

199,04 = 4x ²

Chia cả hai bên cho 4 để được

49,76 = x ²

x = √49,76

x = 7,05

Do đó, các kích thước của hình nón như sau;

Bán kính của hình nón = 7,05 in

Chiều cao nghiêng, l = 3 x 7,05 = 21,15 in

Chiều cao của một, h = √ (21,15 ² – 7,05 ² )

h = 19,94 in.

Ví dụ 5

Diện tích mặt bên nhỏ hơn diện tích mặt bên của hình nón là 177 cm ² . Tìm bán kính của hình nón.

Giải pháp

Tổng diện tích bề mặt của hình nón = Diện tích bề mặt bên + Diện tích cơ sở

Do đó, 177 cm ² = Diện tích cơ sở

Nhưng, diện tích cơ sở của hình nón = πr ²

177 = 3,14r ²

r ² = 56,4 cm

r = √56,4

= 7,5 cm

Vậy, bán kính của hình nón là 7,5 cm.

Ví dụ 6

Chi phí sơn một thùng hình nón là 0,01 đô la cho mỗi cm ² . Tìm tổng chi phí sơn 15 thùng hình nón có bán kính 5 cm và chiều cao nghiêng 8 cm.

Giải pháp

TSA = πr (l + r)

= 3,14 x 5 (5 + 8)

= 15,7 x 13

= 204,1 cm ²

Tổng chi phí sơn 15 container = 204,1 x 0,01 x 15

= $ 30,62

Xem thêm:

Yếu tố và bội số – Sự khác biệt và ví dụ dễ hiểu nhất

Tính diện tích bề mặt của hình khối – Giải thích & ví dụ dễ nhất hiện nay