Tương tự, nếu β và γ lần lượt là góc giữa các cạnh ca và ab thì theo định luật côsin, ta có:
b 2 = a 2 + c 2 – 2ac cos β
c 2 = b 2 + a 2 – 2ab cos γ
| Sự thật: Nếu một trong các góc bất kỳ, α, β hoặc γ bằng 90 độ, thì biểu thức trên sẽ chứng minh cho định lý Pythagoras, vì cos 90 = 0. Do đó, ba phương trình trên có thể được biểu diễn dưới dạng:
a 2 = b 2 + c 2 [nếu α = 90 độ] b 2 = a 2 + c 2 [nếu β = 90 độ] c 2 = b 2 + a 2 [nếu γ = 90 độ] |
Định nghĩa định luật Cosin
Trong Lượng giác, định luật Cosin, còn được gọi là Quy tắc Cosin hoặc Công thức Cosin về cơ bản liên hệ độ dài của tam giác thứ e với cosin của một trong các góc của nó. Nó nói rằng, nếu biết độ dài của hai cạnh và góc giữa chúng đối với một tam giác, thì chúng ta có thể xác định độ dài của cạnh thứ ba. Nó được đưa ra bởi:
c 2 = a 2 + b 2 – 2ab cosγ
Trong đó a, b và c là các cạnh của tam giác và γ là góc giữa a và b. Xem hình bên dưới.
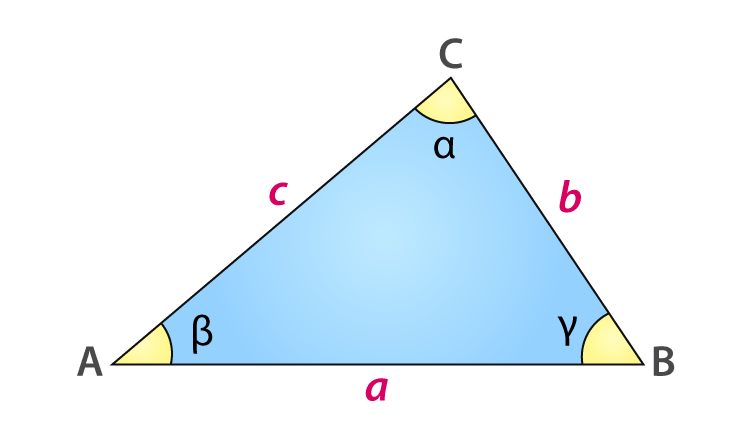

Định luật cosin
Công thức
Theo công thức định luật cosin, để tìm độ dài các cạnh của tam giác ABC, ta có thể viết như sau;
- a 2 = b 2 + c 2 – 2bc cos α
- b 2 = a 2 + c 2 – 2ac cos β
- c 2 = b 2 + a 2 – 2ba cos γ
Và nếu chúng ta muốn tìm các góc của △ ABC, thì quy tắc côsin được áp dụng như;
- cos α = [b 2 + c 2 – a 2 ] / 2bc
- cos β = [a 2 + c 2 – b 2 ] / 2ac
- cos γ = [b 2 + a 2 – c 2 ] / 2ab
Trong đó a, b và c là độ dài các cạnh của tam giác.
Giải quyết tính đồng thời của SSS
Trong tính đồng dư SSS, chúng ta biết độ dài của cả ba cạnh của một tam giác và chúng ta cần tìm số đo của tam giác chưa biết. Do đó, sử dụng định luật cosin, chúng ta có thể tìm được góc khuyết.
Đầu tiên, chúng ta cần tìm một góc bằng cách sử dụng định luật cosin, giả sử cos α = [b 2 + c 2 – a 2 ] / 2bc.
Sau đó, chúng ta sẽ tìm lại góc thứ hai theo định luật tương tự, cos β = [a 2 + c 2 – b 2 ] / 2ac
Bây giờ bạn có thể tìm thấy góc thứ ba đơn giản bằng cách sử dụng tính chất tổng góc của tam giác. Điều đó có nghĩa là tổng của tất cả ba góc của một tam giác bằng 180 độ.
Bằng chứng
Bây giờ chúng ta hãy tìm hiểu luật chứng minh cosin ở đây;
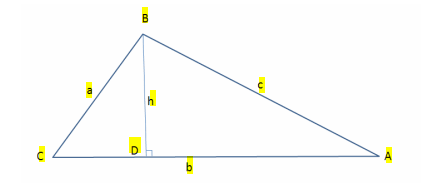

Định luật Cosines Chứng minh
Trong tam giác vuông BCD, theo định nghĩa của hàm số cosin :
cos C = CD / a
hoặc là
CD = a cos C
Trừ phương trình trên khỏi vế b, ta được
DA = b – acosC …… (1)
Trong tam giác BCD, theo định nghĩa sin
sin C = BD / a
hoặc là
BD = a sinC …… (2)
Trong tam giác ADB, nếu chúng ta áp dụng Định lý Pitago , thì
c 2 = BD 2 + DA 2
Thay BD và DA từ phương trình (1) và (2)
c 2 = (a sin C) 2 + (b-accosC) 2
Bằng phép nhân chéo, chúng ta nhận được:
c 2 = a 2 sin 2 C + b 2 – 2abcosC + a 2 cos 2 C
Sắp xếp lại phương trình trên:
c 2 = a 2 sin 2 C + a 2 cos 2 C + b 2 – 2ab cosC
Lấy 2 làm nhân tử chung, chúng ta nhận được;
c 2 = a 2 (sin 2 C + cos 2 C) + b 2 – 2ab cosC
Bây giờ từ phương trình trên, bạn biết rằng,
sin 2 θ + cos 2 θ = 1
∴ c 2 = a 2 + b 2 – 2ab cosC
Do đó, định luật cosin được chứng minh.
Vấn đề và Giải pháp
Chúng ta hãy hiểu khái niệm này bằng cách giải quyết một trong những vấn đề về luật cosin.
Bài toán: Một tam giác ABC có các cạnh a = 10cm, b = 7cm và c = 5cm. Bây giờ, hãy tìm góc ‘x’ của nó.
Giải pháp:
Coi tam giác dưới đây là tam giác ABC, trong đó,
a = 10cm
b = 7cm
c = 5cm
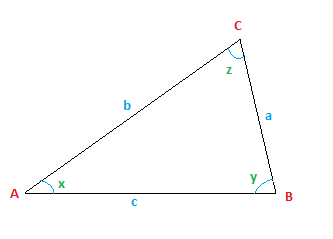

Các vấn đề về luật Cosine
Bằng cách sử dụng luật cosin,
a 2 = b 2 + c 2 – 2bc cos (x)
Hoặc là
cos x = (b 2 + c 2 – a 2 ) / 2bc
Thay giá trị của các cạnh của tam giác tức là a, b và c, ta được
cos (x) = (7 2 + 5 2 – 10 2 ) / (2 × 7 × 5)
cos (x) = (49 + 25 -100) / 70
cos (x) = -0,37
Điều quan trọng là phải giải nhiều bài toán hơn dựa trên công thức luật cosin bằng cách thay đổi giá trị của các cạnh a, b & c và luật kiểm tra chéo của máy tính cosin đã cho ở trên.
Câu hỏi thường gặp – Câu hỏi thường gặp
Định luật cosine là gì?
Định luật cosin phát biểu điều gì?
a 2 = b 2 + c 2 – 2bc cos α
b 2 = a 2 + c 2 – 2ac cos β
c 2 = b 2 + a 2 – 2ba cos γ
trong đó a, b và c là các cạnh của tam giác.
Khi nào chúng ta nên sử dụng định luật cosin?
Chúng ta có thể sử dụng định luật cosin cho tất cả các tam giác không?
Làm thế nào để giải quyết định luật cosin?
a 2 = b 2 + c 2 -2bc cos α
Trong đó a là cạnh chưa biết, b và c là cạnh đã biết của tam giác và α là góc giữa b và c.
Công thức tìm góc sử dụng định luật côsin là gì?
cos α = [b 2 + c 2 – a 2 ] / 2bc
cos β = [a 2 + c 2 – b 2 ] / 2ac
cos γ = [b 2 + a 2 – c 2 ] / 2ab