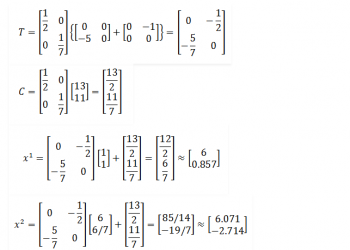Ngoài ra, chúng ta có thể nói, nếu (xa) là một nhân tử của đa thức f (x), thì f (a) = 0. Điều này chứng tỏ nghịch đảo của định lý. Chúng ta hãy xem cách chứng minh định lý này cùng với các ví dụ.

Định lý thừa số là gì?

Định lý thừa số thường được sử dụng để tính nhân tử của một đa thức và tìm nghiệm nguyên của đa thức. Đó là một trường hợp đặc biệt của định lý phần dư đa thức.

Như đã thảo luận trong phần giới thiệu, đa thức f (x) có nhân tử (xa), nếu và chỉ khi, f (a) = 0. Đây là một trong những phương pháp để tính nhân tử của đa thức .

Bằng chứng

Ở đây chúng ta sẽ chứng minh định lý thừa số, theo đó chúng ta có thể suy ra nhân tử của đa thức.

Xét đa thức f (x) chia hết cho (xc) thì f (c) = 0.

Sử dụng định lý phần dư,

f (x) = (xc) q (x) + f (c)

Trong đó f (x) là đa thức đích và q (x) là đa thức thương.

Vì, f (c) = 0, do đó,

f (x) = (xc) q (x) + f (c)

f (x) = (xc) q (x) +0

f (x) = (xc) q (x)

Do đó, (xc) là một nhân tử của đa thức f (x).

Một phương pháp khác

Theo định lý phần dư ,

f (x) = (xc) q (x) + f (c)

Nếu (xc) là một thừa số của f (x) thì phần dư phải bằng không.

(xc) chia chính xác f (x)

Do đó, f (c) = 0.

Các câu lệnh sau đây tương đương với bất kỳ đa thức f (x) nào

• Phần còn lại bằng 0 khi f (x) chia chính xác cho (xc)
• (xc) là một thừa số của f (x)
• c là nghiệm của f (x)
• c là số không của hàm f (x) hoặc f (c) = 0

Cách sử dụng định lý thừa số

Các bước được đưa ra dưới đây để tìm nhân tử của đa thức bằng cách sử dụng định lý nhân tử:

Bước 1: Nếu f (-c) = 0 thì (x + c) là một nhân tử của đa thức f (x).

Bước 2: Nếu p (d / c) = 0 thì (cx-d) là một nhân tử của đa thức f (x).

Bước 3: Nếu p (-d / c) = 0 thì (cx + d) là một nhân tử của đa thức f (x).

Bước 4: Nếu p (c) = 0 và p (d) = 0 thì (xc) và (xd) là nhân tử của đa thức p (x).

Thay vì tìm thừa số bằng phương pháp chia dài đa thức, cách tốt nhất để tìm thừa số là định lý nhân tử và phương pháp chia tổng hợp. Định lý này được sử dụng chủ yếu để loại bỏ các số không đã biết khỏi các đa thức để tất cả các số không chưa biết không bị ghép đôi, do đó bằng cách dễ dàng tìm các số không để tạo ra đa thức bậc thấp hơn.

Có một cách khác để xác định định lý thừa số. Thông thường, khi chia một đa thức cho một nhị thức, chúng ta sẽ nhận được một lời nhắc. Thương số thu được được gọi là đa thức suy giảm khi đa thức đó chia cho một trong các nhân tử của nó. Nếu bạn nhận được phần dư là 0, định lý thừa số được minh họa như sau:

Đa thức, giả sử f (x) có nhân tử (xc) nếu f (c) = 0, trong đó f (x) là đa thức bậc n, trong đó n lớn hơn hoặc bằng 1 với bất kỳ số thực nào, c.

Các phương pháp khác để tìm yếu tố

Ngoài định lý thừa số, có những phương pháp khác để tìm thừa số, chẳng hạn như:

• Phân chia dài đa thức
• Bộ phận tổng hợp

Các vấn đề và giải pháp

Ví dụ và giải pháp định lý thừa số được đưa ra dưới đây. Hãy xem qua một lần và hiểu rõ về định lý này. Định lý thừa số đa thức toán lớp 9 giúp các em nắm được kiến ​​thức về tìm nghiệm nguyên của biểu thức bậc hai và phương trình đa thức, dùng để giải các bài toán phức tạp ở các bậc học cao hơn.

Xét hàm đa thức f (x) = x ² + 2x -15

Các giá trị của x mà f (x) = 0 được gọi là nghiệm nguyên của hàm số.

Giải phương trình, giả sử f (x) = 0, ta được:

x ² + 2x -15 = 0

x ² + 5x – 3x -15 = 0

(x + 5) (x-3) = 0

(x + 5) = 0 hoặc (x-3) = 0

x = -5 hoặc x = 3

Vì (x + 5) và (x-3) là thừa số của x ² + 2x -15 , -5 và 3 là nghiệm của phương trình x ² + 2x -15 = 0 nên chúng ta cũng có thể kiểm tra như sau:

Nếu x = -5 là nghiệm thì

f (x) = x ² + 2x -15

f (-5) = (-5) ² + 2 (-5) – 15

f (-5) = 25-10-15

f (-5) = 25-25

f (-5) = 0

Nếu x = 3 là nghiệm thì;

f (x) = x ² + 2x -15

f (3) = 3 ² +2 (3) – 15

f (3) = 9 +6 -15

f (3) = 15-15

f (3) = 0

Nếu phần dư bằng 0, (xc) là một đa thức của f (x).

Phương pháp thay thế – Phương pháp phân chia tổng hợp

Chúng ta cũng có thể sử dụng phương pháp chia tổng hợp để tìm phần dư.

Xét phương trình đa thức tương tự

f (x) = x ² + 2x -15

Chúng tôi sử dụng 3 ở bên trái trong phương pháp chia tổng hợp cùng với các hệ số 1,2 và -15 từ phương trình đa thức đã cho.

Vì phần dư bằng 0 nên 3 là nghiệm của đa thức đã cho.

Các kỹ thuật được sử dụng để giải phương trình đa thức bậc 3 trở lên không đơn giản như vậy. Vì vậy phương trình tuyến tính và bậc hai được sử dụng để giải phương trình đa thức.