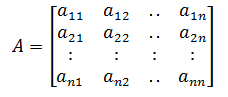
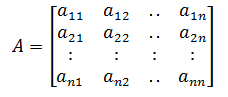
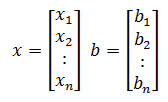
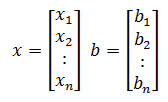
Chúng ta hãy phân tích ma trận A thành một thành phần đường chéo D và phần dư R sao cho A = D + R.
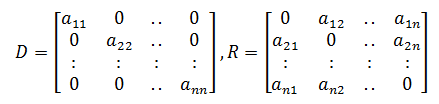
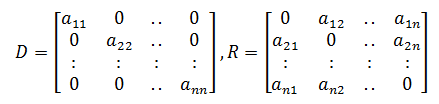
Lặp lại giải pháp sẽ nhận được bằng cách sử dụng phương trình dưới đây.
x (k + 1) = D -1 (b – Rx (k) )
Đây,
x k = lần lặp thứ k hoặc tính gần đúng của x
x (k + 1) = Lần lặp tiếp theo của x k hoặc (k + 1) lần lặp thứ của x
Công thức cho phương pháp dựa trên phần tử được đưa ra là
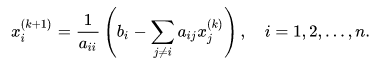
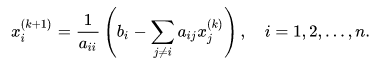
Đọc thêm:
Ma trận đường chéo
Ma trận tam giác trên
Ma trận nghịch đảo
Ma trận cho lớp 12
Công thức phương pháp Jacobian
Cho một xấp xỉ chính xác x (k) = (x 1 (k) , x 2 (k) , x 3 (k) ,…, x n (k) ) cho x, quy trình của phương pháp Jacobian giúp sử dụng phương trình đầu tiên và giá trị hiện tại của x 2 (k) , x 3 (k) ,…, x n (k) để tính giá trị mới x 1 (k + 1) . Tương tự như vậy, để đánh giá một giá trị mới x i (k) bằng cách sử dụng phương trình thứ i và các giá trị cũ của các biến khác. Nghĩa là, các giá trị hiện tại đã cho x (k) = (x 1 (k) , x2 (k) ,…, x n (k) ), xác định các giá trị mới bằng cách giải cho x (k + 1) = (x 1 (k + 1) , x 2 (k + 1) ,…, x n (k +1) ) trong biểu thức dưới đây của phương trình tuyến tính .
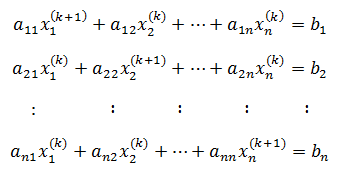
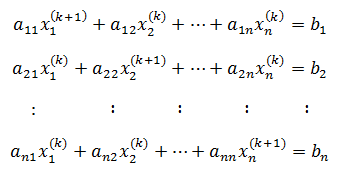
Hệ phương trình trên cũng có thể được viết như dưới đây.
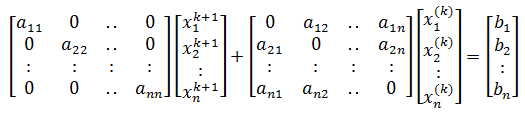
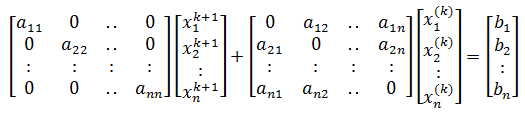
Từ biểu thức trên, rõ ràng rằng, chỉ số con i chỉ ra rằng x i (k) là phần tử thứ i của vectơ x (k) = (x 1 (k) , x 2 (k) ,…, x i (k ) ,…, X n (k) ), và chỉ số trên k tương ứng với lần lặp cụ thể (không phải lũy thừa thứ k của x i ).
Giả sử rằng D, U và L lần lượt đại diện cho đường chéo, tam giác trên nghiêm ngặt và tam giác dưới nghiêm ngặt và các phần của ma trận A, khi đó phương pháp của Jacobian có thể được mô tả trong ký hiệu vectơ ma trận như cho dưới đây.
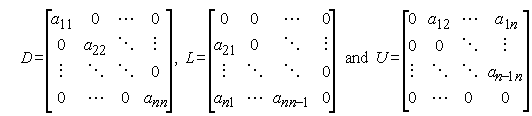

Điều này có thể được đơn giản hóa như hình dưới đây.
Dx (k + 1) + (L + U) x (k) = b
x (k + 1) = D -1 [(-LU) x (k) + b]
Thuộc tính của phương pháp Jacobian
Thêm các ứng dụng của ma trận Jacobian trong các lĩnh vực khác nhau, phương pháp này giữ một số thuộc tính quan trọng. Sự đơn giản của phương pháp này được xem xét trên cả hai khía cạnh tốt và xấu. Phương pháp này có thể nói là tốt vì nó là phương pháp lặp đầu tiên và dễ hiểu. Tuy nhiên, phương pháp này cũng được coi là không tốt vì nó thường không được sử dụng trong thực tế. Mặc dù có những nhược điểm, nó vẫn là một điểm khởi đầu tốt cho những ai sẵn sàng học các phương pháp lặp lại hữu ích hơn nhưng phức tạp hơn.
Ví dụ về phương pháp Jacobian
Dưới đây là một hệ phương trình tuyến tính có dạng Ax = b với ước lượng ban đầu x (0) .
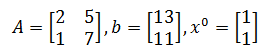
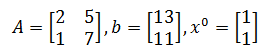
Giải quyết vấn đề trên bằng phương pháp Jacobian.
Giải pháp:
Được,
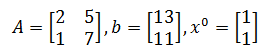
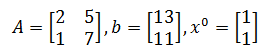
Chúng ta biết rằng x (k + 1) = D -1 (b – Rx (k) ) được sử dụng để ước lượng x.
Chúng ta hãy viết lại biểu thức trên ở dạng thuận tiện hơn, tức là D -1 (b – Rx (k) ) = Tx (k) + C
Đây,
T = -D -1 R
C = D -1 b
R = L + U
Hãy để chúng tôi chia ma trận A dưới dạng ma trận đường chéo và phần dư.
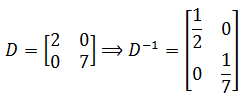
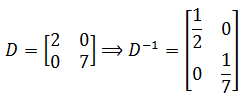
Phần trên và phần dưới của lời nhắc A:
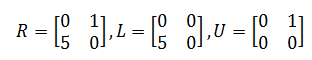
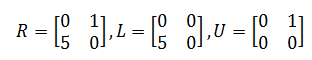
Đây,
R = Ma trận phần dư
L = Phần dưới của R
U = Phần trên của R
T = -D -1 (L + U) = D -1 [-L + (-U)]
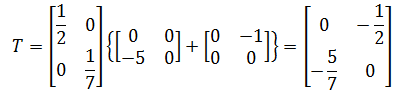
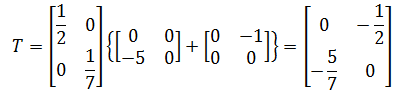
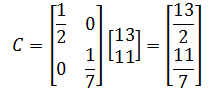
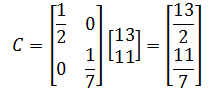
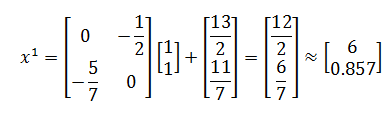
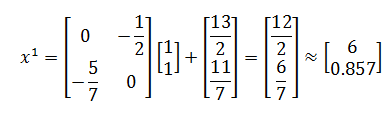
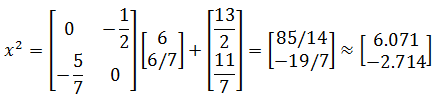
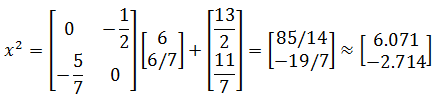
Lặp lại quá trình trên cho đến khi nó hội tụ, tức là cho đến khi giá trị của || Ax n – b || nhỏ.