Contents
Định nghĩa của Hàm hợp lý
Một số có thể được biểu thị dưới dạng pq trong đó p và q là các số nguyên và q ≠ 0, là một số hữu tỉ.
Cũng giống như số hữu tỉ, định nghĩa hàm hữu tỉ như sau:
Định nghĩa : Hàm hữu tỉ R (x) là hàm có dạngP( x )Q ( x ) trong đó P (x) và Q (x) là các hàm đa thức và Q (x) là một đa thức khác 0.
R (x) = P( x )Q ( x ), Q (x) ≠ 0
Từ điều kiện đã cho đối với Q (x), chúng ta có thể kết luận rằng các số 0 của hàm đa thức ở mẫu số không thuộc miền của hàm. Khi Q (x) = 1, tức là hàm đa thức không đổi, hàm hữu tỉ trở thành hàm đa thức.
Lập đồ thị các hàm hợp lý
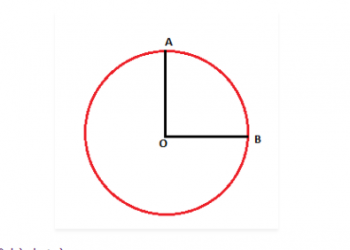
Một khái niệm rất quan trọng để vẽ đồ thị các hàm hợp lý là biết về không triệu chứng của chúng. Đường tiệm cận là một đường hoặc đường cong tiếp cận đường cong một cách ngu ngốc mãi mãi nhưng chưa bao giờ chạm vào nó. Trong bộ lễ phục. 1, một ví dụ về không triệu chứng được đưa ra.


Hình 1: Không có triệu chứng
Dấu hiệu của Hàm hợp lý
Các hàm hợp lý có thể có 3 loại không triệu chứng:
- Theo chiều ngang Asymptotes
- Các asymptotes dọc
- Xiên Asymptote
Theo chiều ngang Asymptotes
Điều này có nghĩa đen là đường tiệm cận nằm ngang, tức là song song với trục của biến độc lập. R (x) chỉ có thể có một tiệm cận ngang nếu
Mức độ P (x) ≤ Mức độ Q (x)
Để xác định các dấu không triệu chứng, hãy chia tử số và mẫu số của R (x) cho xD e gr e e o f Q ( x ). Sau đó, tìm giá trị mà R (x) tiếp cận vì x có xu hướng đạt giá trị rất lớn. Giá trị này cho biết chiều cao của đường tiệm cận.
Mối quan hệ lặp lại là gì? Xem xong 5 phút hiểu luôn.
Các asymptotes dọc
R (x) sẽ có các dấu không triệu chứng thẳng đứng tại các số không của Q (x). Điều này là do tại các số không của Q (x), Q (x) = 0. Điều này có nghĩa là chỉ cần về phía bên trái và bên phải của số không của Q (x), giá trị của Q sẽ là số âm và số dương tương ứng rất nhỏ. Giá trị của R (x) sẽ là một số âm và dương tương ứng, về phía bên trái và bên phải của điểm đó.
Dấu hiệu xiên
R (x) sẽ có tiệm cận xiên nếu nó có thể được biểu diễn dưới dạng T( x ) + 1Q ( x ).
Khi Q (x) ≫ 0 thì R (x) ≈ T (x). Do đó, đường cong hoặc đường thẳng T (x) trở thành một tiệm cận xiên.
Để trích dẫn một ví dụ, chúng ta hãy lấy R (x) = x2+ 3 x + 3x + 1.
Ở đây, tung độ của P (x) lớn hơn của Q (x). Vì vậy, nó không thể có một tiệm cận ngang. Nhưng nó sẽ có tiệm cận đứng tại x = -1. Điều này là do điểm đó là 0 của đa thức mẫu số của nó.
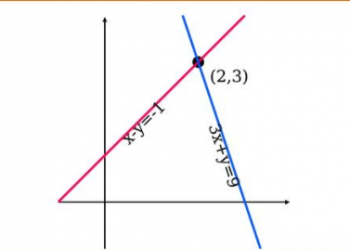
Nó cũng có thể được viết là R (x) = ( x + 2 ) + 1x + 1. Vì vậy, khi x ≫ 0, R (x) ≈ x + 2. Vì vậy, y = x + 2 sẽ là một tiệm cận xiên. Đồ thị của hàm và tất cả các hàm không có dấu hiệu được hiển thị trong hình. 2.


Hình 2: Một hàm hợp lý với các dấu không của nó
Xem thêm: