Hàm tuần hoàn

Trong toán học, một hàm tuần hoàn là hàm số lặp lại giá trị của nó trong những khoảng đều đặn hay chu kỳ. tỉ dụ quan trọng nhất của những hàm tuần hoàn đó là các hàm lượng giác, nhưng mà lặp lại trong khoảng 2π radian. Hàm tuần hoàn được dùng thường xuyên để miêu tả các dao động, sóng, và những hiện tượng khác thể hiện tính tuần hoàn.

Định nghĩa hàm tuần hoàn

Hàm số f được nói là tuần hoàn nếu đối với hằng số khác 0 P, ta có

đối với mọi x trong miền xác định. Hằng số P khác 0 được gọi là chu kỳ của hàm số. Nếu sống sót ít nhất^[1] một hằng số P có thuộc tính này, nó được gọi là chu kỳ căn bản (hoặc chu kỳ cơ sở, chu kỳ gốc.) phổ biến, khi nhắc tới chu kỳ của hàm số thì được hiểu là chu kỳ căn bản của nó. Một hàm số với chu kỳ P sẽ lặp lại trên những khoảng có độ dài P lần, và những khoảng này thỉnh thoảng cũng được coi là chu kỳ của hàm số.

Về mặt hình học, hàm số tuần hoàn có thể được định nghĩa như là một hàm nhưng đồ thị của nó biểu lộ đối xứng tịnh tiến. chi tiết, một hàm f tuần hoàn theo chu kỳ P nếu đồ thị của f là định hình dưới phép tịnh tiến theo hướng x bởi vì một khoảng cách P.

khái niệm về tính tuần hoàn này có thể mở mang ra cho những đối tượng hình học khác, cũng như tổng quát hóa cho nhiều chiều, tỉ dụ như lát mặt phẳng bằng lưới hình (tessellation). Một dãy có thể coi như một hàm có miền xác định trên các số tự nhiên, và một dãy tuần hoàn làm theo khái niệm ở trên.

xem thêm

Công thức tính diện tích mặt cầu ngoại tiếp

Xét sự biến thiên của hàm số

Cách soạn bài Con rồng cháu Tiên

Toàn bộ công thức Toán lớp 12

2. Một số tỉ dụ.

thí dụ 1. Chứng minh rằng hàm số f (x) = sin(x) là hàm tuần hoàn với chu kỳ $T=2\pi.$

Giải. Ta có

– Tập xác định của hàm số là D = R

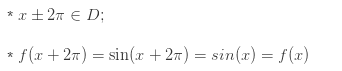
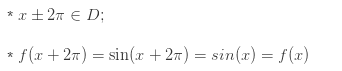
– Rõ ràng với mọi  ta có

Suy ra, hàm số f (x) = sin(x) là hàm tuần hoàn.

Bậy giờ ta chứng minh  là chu kỳ. Thật vậy, giả sử còn sinh tồn số dương  bé dại hơn  sao cho với mọi  ta có

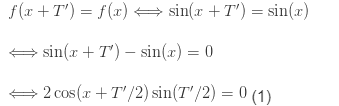
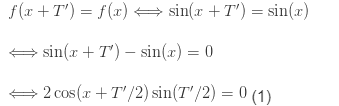
bởi vì (1) đúng với mọi  nên suy ra

nhưng điều này không xảy ra. bởi thế  là chu kỳ của hàm số y = sin(x)