Ngoài ra, hãy đọc:
Phương trình hồi quy tuyến tính
Thước đo mức độ của mối quan hệ giữa hai biến được thể hiện bằng hệ số tương quan . Phạm vi của hệ số này nằm trong khoảng từ -1 đến +1. Hệ số này cho thấy mức độ liên kết của dữ liệu quan sát đối với hai biến.
Phương trình đường hồi quy tuyến tính được viết dưới dạng:
Y = a + bX
trong đó X là biến độc lập và được vẽ dọc theo trục x
Y là biến phụ thuộc và được vẽ dọc theo trục y
Hệ số góc của đường thẳng là b và a là điểm giao nhau (giá trị của y khi x = 0).
Công thức hồi quy tuyến tính
Hồi quy tuyến tính cho thấy mối quan hệ tuyến tính giữa hai biến. Phương trình hồi quy tuyến tính tương tự như công thức hệ số góc mà chúng ta đã học ở các lớp trước đó, chẳng hạn như phương trình tuyến tính hai biến . Nó được đưa ra bởi;
Y = a + bX
Bây giờ, ở đây chúng ta cần tìm giá trị của hệ số góc của đường thẳng b, được vẽ trong biểu đồ phân tán và giao điểm, a.


Hồi quy tuyến tính cơ bản
Trường hợp đơn giản nhất của một biến dự báo vô hướng duy nhất x và một biến phản hồi vô hướng duy nhất y được gọi là hồi quy tuyến tính đơn giản. Phương trình cho hồi quy này được biểu diễn bằng;
y = a + bx
Việc mở rộng thành các biến dự báo có giá trị bằng véc tơ và nhiều biến được gọi là hồi quy tuyến tính nhiều biến , còn được gọi là hồi quy tuyến tính đa biến. Phương trình cho hồi quy này được biểu diễn bằng;
Y = a + bX
Hầu hết tất cả các mẫu hồi quy trong thế giới thực đều bao gồm nhiều yếu tố dự đoán và các giải thích cơ bản về hồi quy tuyến tính thường được giải thích dưới dạng hình thức hồi quy bội. Tuy nhiên, lưu ý rằng trong những trường hợp này, biến phụ thuộc y vẫn là một đại lượng vô hướng.
Đường hồi quy hình vuông nhỏ nhất hoặc Đường hồi quy tuyến tính
Phương pháp phổ biến nhất để điều chỉnh một đường hồi quy trong biểu đồ XY là phương pháp bình phương nhỏ nhất. Quá trình này xác định dòng phù hợp nhất cho dữ liệu được lưu ý bằng cách giảm tổng bình phương của độ lệch dọc từ mỗi điểm dữ liệu xuống dòng. Nếu một điểm nằm trên đường vừa khít chính xác, thì độ lệch vuông góc của nó là 0. Bởi vì các biến thể được bình phương đầu tiên, sau đó được thêm vào, các giá trị âm và dương của chúng sẽ không bị hủy bỏ.
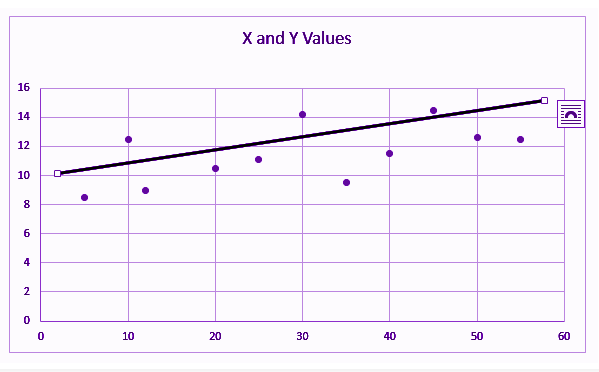

Hồi quy tuyến tính xác định đường thẳng, được gọi là đường hồi quy bình phương nhỏ nhất hoặc LSRL, thể hiện tốt nhất các quan sát trong phân tích hai biến của tập dữ liệu. Giả sử Y là một biến phụ thuộc và X là một biến độc lập, khi đó đường hồi quy tổng thể được cho bởi;
Y = B 0 + B 1 X
Ở đâu
B 0 là một hằng số
B 1 là hệ số hồi quy
Nếu một mẫu quan sát ngẫu nhiên được đưa ra, thì đường hồi quy được biểu thị bằng;
ŷ = b 0 + b 1 x
trong đó b 0 là hằng số, b 1 là hệ số hồi quy, x là biến độc lập và ŷ là giá trị dự đoán của biến phụ thuộc.
Thuộc tính của hồi quy tuyến tính
Đối với đường hồi quy trong đó các tham số hồi quy b 0 và b 1 được xác định, các thuộc tính được đưa ra như sau:
- Đường này làm giảm tổng bình phương của sự khác biệt giữa các giá trị quan sát và giá trị dự đoán.
- Đường hồi quy đi qua giá trị trung bình của các giá trị biến X và Y
- Hằng số hồi quy (b 0 ) bằng y-intercept của hồi quy tuyến tính
- Hệ số hồi quy (b 1 ) là độ dốc của đường hồi quy bằng mức thay đổi trung bình của biến phụ thuộc (Y) đối với sự thay đổi đơn vị trong biến độc lập (X).
Hệ số hồi quy
Trong đường hồi quy tuyến tính, chúng ta đã thấy phương trình được cho bởi;
Y = B 0 + B 1 X
Ở đâu
B 0 là một hằng số
B 1 là hệ số hồi quy
Bây giờ, chúng ta hãy xem công thức để tìm giá trị của hệ số hồi quy.
B 1 = b 1 = Σ [(x i – x) (y i – y)] / Σ [(x i – x) 2 ]
Trong đó x i và y i là các tập dữ liệu được quan sát.
Và x và y là giá trị trung bình.
Xem thêm: