Phần Công thức & Phần Conic là gì? Xem xong 5 phút hiểu luôn.

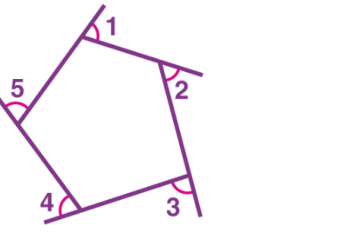
M( x , y) = (mx2+ nx1m + n,mY2+ nY1m + n)

Chứng minh cho Công thức Phần

Gọi P (x ₁ , y ₁ ) và Q (x ₂ , y ₂ ) là hai điểm trong mặt phẳng xy – lanh . Gọi M (x, y)  là điểm chia đoạn thẳng PQ  theo tỉ lệ m: n .

PA, MN và QR  được vẽ vuông góc với trục x.

PS  và MB được vẽ song song với trục x .

∠MPS = ∠QMB (góc tương ứng)

∠MSP = ∠QBM = 90 °

Theo tiêu chí tương tự AA,

ΔPMS ~ ΔMQB

⇒ PMMQ = PSMB = MSQ B = mn – (1)

PS = AN = ON – OA = x – x ₁

MB = NR = HOẶC – BẬT = x ₂ – x

MS = MN – SN = y – y ₁

QB = RQ – RB = y ₂ – y

Từ phương trình (1),

mn = x –  x1x2 – x  = Y – Y1Y2 – và 

⇒ mn = x –  x1x2 – x 

⇒ x  = mx2 + n x1m + n  

Tương tự,

mn = Y – Y1Y2 – và 

⇒ y  = mY2 + n Y1m + n  

Vì vậy, tọa độ của điểm M( x , y) phân chia các điểm nối đoạn thẳng P(x1,Y1) và Q (x2,Y2) nội bộ trong tỷ lệ m : n Chúng tôi

(mx2 + n x1m + n  ,mY2 + n Y1m + n  )

Đây được gọi là công thức phần .

Công thức phần (Bên ngoài):

Công thức phần cũng có thể được sử dụng để tìm tọa độ của một điểm nằm ngoài đoạn thẳng, trong đó tỷ lệ độ dài của một điểm từ cả hai đoạn thẳng theo tỷ lệ m: n.

Công thức Phần được đưa ra như sau: (mx2– nx1m – n,mY2– nY1m – n)

Hãy cho chúng tôi hiểu đó là bằng chứng với một Ví dụ:

Xét một điểm A (x ₁ , y ₁ ).

C (x, y)  là một điểm chia đoạn thẳng OA  theo tỉ lệ 2: 1 , trong đó điểm O là gốc tọa độ.

⇒ OC : CA = 2 : 1

Để tìm tọa độ điểm C , người ta vẽ ba đường thẳng CD, AB và CE sao cho CD và AB vuông góc với trục x và  CE  song song với trục x .

∠COD = ∠ACE (góc tương ứng)

∠CDO = ∠AEC = 90 °

Theo tiêu chí AA về độ đồng dạng của hai tam giác,

ΔOCD ~ Δ CAE

Vì vậy, tỷ lệ các cạnh tương ứng sẽ bằng nhau, tức là

Ô CCA = CDA E = Về DCE              – (1)

Vì tọa độ của  C  là ( x, y ),

OD = x đơn vị

BE = CD = y đơn vị

CE = BD = OB – OD = (x ₁ – x) đơn vị
AE = AB – BE = (y ₁ – y) đơn vị
Ngoài ra, OC: CA = 2: 1
⇒ OC = 2a đơn vị
Và
CA = a đơn vị
Trong đó a là một hằng số.

Phương trình (1) trở thành

2 aa = xx1 – x  = YY1 – và 

xx1 – x  = 2

⇒ x  = 2 (x1 – x ) 

⇒ 3 x  = 2x1

⇒ x  = 23 x1

Tương tự,

YY1 – và  = 2

⇒ 3 năm  = 2Y1

Y = 23 Y1

Do đó, tọa độ của điểm C là (23 x1,23 Y1).

Mối quan hệ lặp lại là gì? Xem xong 5 phút hiểu luôn.

Phần Công thức cho Lớp 10

Tọa độ của điểm A (x, y) chia đoạn thẳng nối các điểm P (x ₁ , y ₁ ) và Q (x ₂ , y ₂ ) theo tỉ lệ m ₁ : m ₂ được cho bởi công thức :
P (x, y) =(m1x2+m2x1m1+m2,m1Y2+m2Y1m1+m2)

Tương tự, nếu điểm P chia đoạn thẳng nối A và B ra bên ngoài theo tỷ lệ m ₁ : m ₂ thì tọa độ của điểm là:
P (x, y) =(m1x2–m2x1m1–m2,m1Y2–m2Y1m1–m2)

Nếu điểm M chia đoạn thẳng nối các điểm P (x ₁ , y ₁ ) và Q (x ₂ , y ₂ ) theo tỉ lệ k: 1 thì tọa độ của M sẽ là:

M (x, y) = (kx2 + x1k + 1  ,kY2 + Y1k + 1  )

Tương tự, công thức cho phép chia bên ngoài là:

M (x, y) = (kx2 – x1k – 1  ,kY2 – Y1k – 1  )

Trương hợp đặc biệt:

Điều gì xảy ra nếu điểm Mphân chia các điểm nối đoạn thẳngP(x1,Y1) và Q (x2,Y2) là trung điểm của đoạn thẳng PQ?

Nếu M là điểm giữa, sau đó M chia đoạn thẳng PQ theo tỷ lệ 1 : 1, I E m = n = 1.

Tọa độ của điểm M Chúng tôi

(1 ×  x2 + 1 ×   x11 + 1  ,1 ×  Y2 + 1 ×   Y11 + 1  )

Do đó, tọa độ của một điểm là trung điểm của các điểm nối đoạn thẳng(x1,Y1) và Q (x2,Y2) Chúng tôi,

(x1 + x22,Y1 + Y22)

Ví dụ về Công thức Phần

Ví dụ 1: Tìm tọa độ của điểm chia đoạn thẳng nối các điểm (4,6) và (-5, -4) vào trong theo tỷ lệ 3: 2.

Giải: Gọi P (x, y) là điểm chia đoạn thẳng nối A (4, 6) và B (-5, -4) vào trong theo tỉ lệ 3: 2.

Đây,

(x ₁ , y ₁ ) = (4, 6)

(x ₂ , y ₂ ) = (-5, -4)

m: n = 3: 2

Sử dụng công thức phần,

P (x, y) = (mx2 + n x1m + n  ,mY2 + n Y1m + n  )

Tọa độ của P Chúng tôi,

x = 3 × – 5 + 2 × 4       3 + 2            Y = 3 × – 4 + 2 × 6      3 + 2  

⇒ x  = – 15 + 8  5           ⇒ y  = – 12 + 12  5

⇒ x  = –75                  ⇒ y  = 0

Ví dụ 2: 4 đỉnh của hình bình hành là A (-2, 3), B (3, -1), C (p, q) và D (-1, 9). Tìm giá trị của p và q.

Bài giải:  Các đỉnh của hình bình hành đã cho là:

A (-2, 3), B (3, -1), C (p, q) và D (-1, 9)

Chúng ta biết rằng các đường chéo của một hình bình hành phân giác nhau.

Gọi O là điểm mà các đường chéo cắt nhau.

Tọa độ trung điểm của cả hai A C←→ và B D←→ sẽ giống nhau.

Vì thế,

Sử dụng công thức phần trung điểm,

(x1 + x22,Y1 + Y22)

– 2 + p  2 = – 1 + 32

⇒ – 2 + p    = 2

p = 2 + 2

p = 4

Tương tự,

3 + q  2 = 9 – 1  2

3 + q   = số 8

q = 8 – 3

q = 5

Xem thêm: 

• Giây 90 là gì? Xem xong 5 phút hiểu luôn.
• Phần Công Thức Trong Đại Số Vectơ là gì? Xem xong 5 phút hiểu luôn.