Phân số là gì? Xem xong 5 phút hiểu luôn.

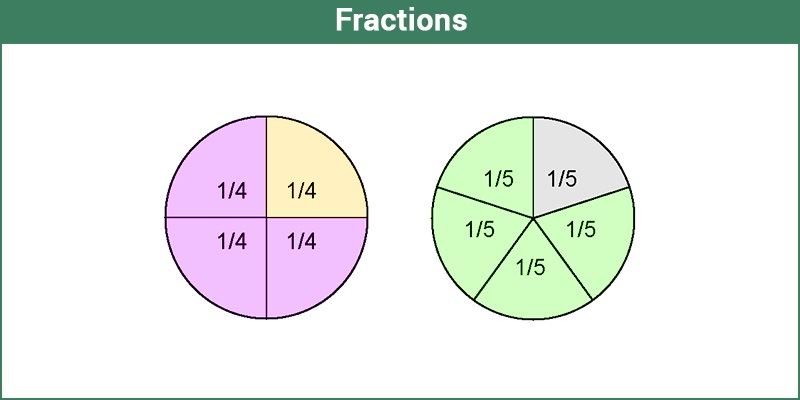
Định nghĩa phân số

Một phân số đại diện cho một giá trị số, xác định các phần của một tổng thể. Giả sử một số phải được chia thành bốn phần, thì nó được biểu diễn dưới dạng x / 4. Vì vậy, phân số ở đây, x / 4, xác định 1/4 của số x. Phân số là một phần quan trọng trong cuộc sống hàng ngày của chúng ta. Có rất nhiều ví dụ về phân số mà bạn sẽ gặp trong cuộc sống thực. Chúng ta phải sẵn sàng hoặc không muốn chia sẻ chiếc bánh pizza ngon đó giữa bạn bè và gia đình của chúng ta. Ba người, bốn lát.

Nếu bạn học và hình dung các phân số một cách dễ dàng, nó sẽ vui hơn và thú vị hơn. Cắt một quả táo, và chúng tôi nhận được các phân số.

Loại phân số

Dựa vào tính chất của tử số và mẫu số, người ta chia phân số thành nhiều dạng khác nhau. Họ đang:

• Phân số thích hợp
• Các phân số không thích hợp
• Phân số hỗn hợp
• Giống như phân số
• Không giống như phân số
• Phân số tương đương

Phân số thích hợp

Các phân số thích hợp là những phân số mà tử số nhỏ hơn mẫu số. Ví dụ, 8/9 sẽ là một phân số thích hợp vì “tử số <mẫu số”.

Các phân số không thích hợp

Phân số không đúng là phân số mà tử số lớn hơn mẫu số. Ví dụ: 9/8 sẽ là một phân số không đúng vì “mẫu số <tử số”.

Phân số hỗn hợp

Một phân số hỗn hợp là sự kết hợp của phần nguyên và một phân số thích hợp. Chúng còn được gọi là hỗn số hoặc hỗn số. Ví dụ:

Giống như phân số

Giống như phân số là những phân số, như tên cho thấy, giống nhau hoặc giống nhau.

Ví dụ, lấy ½ và 2/4; chúng giống nhau vì nếu bạn đơn giản hóa nó về mặt toán học, bạn sẽ nhận được cùng một phân số.

Không giống như phân số

Không giống như phân số, là những phân số khác nhau.

Ví dụ, ½ và 1/3 không giống như phân số.

Phân số tương đương

Hai phân số tương đương với nhau nếu sau khi đơn giản hóa một trong hai phân số bằng phân số kia.

Ví dụ, ⅔ và 4/6 là các phân số tương đương.

Vì, 4/6 = (2 × 2) / (2 × 3) = 2/3

Phân số đơn vị

Một phân số được gọi là một phân số đơn vị, khi tử số bằng 1.

• Một nửa của tổng thể = ½
• Một phần ba của toàn bộ = 1/3
• Một phần tư toàn bộ = ¼
• Một phần năm của toàn bộ =

Tính chất

Tương tự như số thực và số nguyên, số phân số cũng có một số thuộc tính quan trọng. Họ đang:

• Các thuộc tính giao hoán và kết hợp đúng với phép cộng và phép nhân phân số
• Phần tử đồng nhất của phép cộng phân số là 0 và phép nhân phân số là 1
• Nghịch đảo nhân của a / b là b / a, trong đó a và b phải là các phần tử khác không
• Số phân số tuân theo thuộc tính phân phối của phép nhân hơn phép cộng

Quy tắc phân số

Có một số quy tắc chúng ta nên biết trước khi giải các bài toán dựa trên phân số.

Quy tắc số 1: Trước khi cộng hoặc trừ các phân số, chúng ta nên đảm bảo rằng các mẫu số bằng nhau. Do đó, có thể cộng và trừ các phân số với một mẫu số chung.

Quy tắc số 2: Khi chúng ta nhân hai phân số, thì tử số được nhân cũng như mẫu số được nhân lên. Sau đó đơn giản hóa phân số.

Quy tắc số 3: Khi chúng ta chia một phân số cho một phân số khác, chúng ta phải tìm số nghịch đảo của một phân số khác và sau đó nhân với phân số đầu tiên để nhận được câu trả lời.

Thêm phân số

Phép cộng các phân số rất dễ dàng khi chúng có mẫu số chung.

Ví dụ: ⅔ + 8/3 = (2 + 8) / 3 = 10/3

Do đó, chúng ta chỉ cần thêm các tử số ở đây.

Thêm bằng các mẫu số khác nhau

Nếu mẫu số của hai phân số khác nhau, chúng ta phải đơn giản hóa chúng bằng cách tìm LCM của các mẫu số và sau đó làm cho nó chung cho cả hai phân số.

Ví dụ: ⅔ + ¾

Hai mẫu số là 3 và 4

Do đó, LCM của 3 và 4 = 12

Do đó, nhân ⅔ với 4/4 và ¾ với 3/3, ta được;

8/12 + 9/12

= (8 + 9) / 12

= 17/12

Trừ phân số

Quy tắc trừ hai hay nhiều phân số cũng giống như quy tắc cộng. Các mẫu số phải là chung để trừ hai phân số.

Ví dụ: 9/2 – 7/2 = (9-7) / 2 = 2/2 = 1

Trừ với các mẫu số khác nhau

Nếu mẫu số của hai phân số khác nhau, chúng ta phải đơn giản hóa chúng bằng cách tìm LCM của các mẫu số và sau đó làm cho nó chung cho cả hai phân số.

Ví dụ: ⅔ – ¾

Hai mẫu số là 3 và 4

Do đó, LCM của 3 và 4 = 12

Do đó, nhân ⅔ với 4/4 và ¾ với 3/3, ta được;

8/12 – 9/12

= (8-9) / 12

= -1/12

Phép nhân phân số

Theo quy tắc số 2, chúng ta đã thảo luận trong phần trước, khi hai phân số được nhân với nhau, thì phần trên cùng (tử số) và phần dưới cùng (mẫu số) được nhân với nhau.

Nếu a / b và c / d là hai phân số khác nhau thì phép nhân a / b và c / d sẽ là:

(a / b) x (c / d) = (axc) / (bxd) = (ac / bd)

Ví dụ: Nhân ⅔ với 3/7.

(⅔) x (3/7) = (2 × 3) / (3 × 7) = 2/7

Phân chia các phân số

Nếu chúng ta phải chia hai phân số bất kỳ, thì ở đây chúng ta sẽ sử dụng quy tắc 3 từ phần trên, trong đó chúng ta cần nhân phân số thứ nhất với nghịch đảo của phân số thứ hai.

Nếu a / b và c / d là hai phân số khác nhau thì phép chia a / b cho c / d có thể được biểu diễn thành:

(a / b) ÷ (c / d) = (a / b) x (d / c) = (ad / bc)

Ví dụ: Chia ⅔ cho 3/7.

(⅔) ÷ (3/7) = (⅔) x (7/3) = (2 × 7) / (3 × 3) = 14/9

Ví dụ trong đời thực về phân số

Hãy để chúng tôi hình dung một số ví dụ về phân số:

1. Hãy tưởng tượng một chiếc bánh có bốn lát. Lấy hai lát bánh cho chính mình có nghĩa là bạn có hai trong số bốn. Do đó, bạn đại diện cho nó là 2/4.
2. Đổ đầy nửa cốc nước. Bạn thấy gì? 1/2 ly là đầy. Hoặc 1/2 ly đã cạn. 1/2 này là phân số trong đó 1 là tử số, là số phần chúng ta có. Và 2 là mẫu số, số phần của toàn bộ ly được chia thành.

Phân số thành số thập phân

Như chúng ta đã học đủ về phân số, là một phần của tổng thể. Số thập phân là các số được biểu thị dưới dạng thập phân biểu thị phân số, sau khi chia.

Ví dụ: Phân số 1/2 có thể được viết dưới dạng thập phân là 0,5.

Phần tốt nhất của số thập phân là chúng có thể dễ dàng được sử dụng cho bất kỳ phép tính số học nào như cộng, trừ, v.v. Trong khi đôi khi rất khó thực hiện các phép toán trên phân số. Chúng ta hãy lấy một ví dụ để hiểu rõ;

Ví dụ: Thêm 1/6 và 1/4.

giải: 1/6 = 0,17 và 1/4 = 0,25

Do đó, khi thêm 0,17 và 0,25, chúng ta nhận được;

0,17 + 0,25 = 0,42

Các ví dụ đã giải quyết

Câu 1: 12/6 có phải là phân số không? 

Giải pháp: Vâng, đúng như vậy. Nó được gọi là một phân số không đúng.

Câu 2: Chuyển 130.1200 thành phân số.

Giải pháp: Ở đây sẽ sử dụng khái niệm về cách chuyển số thập phân thành phân số

130.1200 = 130.1200 / 10000

= 13012/100

Câu 3: Thêm 3/5 và 15/10.

Giải pháp:

3/5 + 10/15

LCM của 5 và 15 là 15

= (9 + 10) / 15

= 19/15

Bảng tính phân số

Giải quyết vấn đề sau:

1. 3/7 + 9 / 2-8
2. 22/7 + 8/11
3. 32/9 x 81/4
4. 44/9 ÷ 36/4