Định nghĩa
Một phương trình được cho là phương trình tuyến tính hai biến nếu nó được viết dưới dạng ax + by + c = 0, trong đó a, b & c là các số thực và các hệ số của x và y, tức là a và b tương ứng, không bằng không.
Ví dụ, 10x + 4y = 3 và -x + 5y = 2 là các phương trình tuyến tính hai biến.
Nghiệm cho một phương trình như vậy là một cặp giá trị, một cho x và một cho y, điều này làm cho hai vế của một phương trình bằng nhau.
Lời giải của phương trình tuyến tính trong hai biến
Nghiệm của phương trình tuyến tính theo hai biến, ax + by = c, là một điểm cụ thể trong đồ thị, sao cho khi tọa độ x nhân với a và tọa độ y nhân với b, thì tổng của hai giá trị này sẽ bằng c.
Về cơ bản, đối với phương trình tuyến tính hai biến, có vô số nghiệm.
Thí dụ
Để tìm nghiệm của phương trình Tuyến tính 2 biến, chúng ta cần biết hai phương trình.
Hãy xem xét ví dụ:
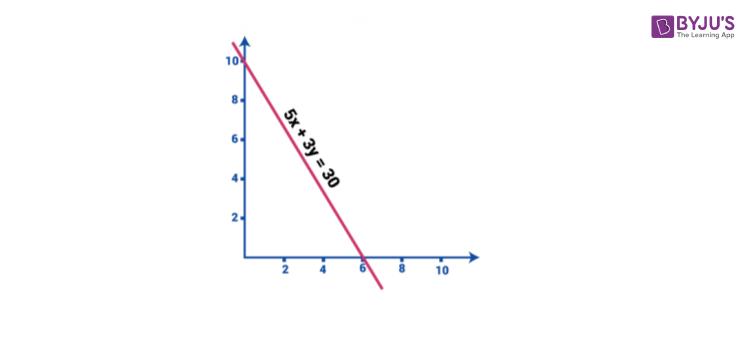
5x + 3y = 30
Phương trình trên có hai biến là x và y.
Bằng đồ thị, phương trình này có thể được biểu diễn bằng cách thay các biến bằng không.
Giá trị của x khi y = 0 là
5x + 3 (0) = 30
⇒ x = 6
và giá trị của y khi x = 0 là,
5 (0) + 3y = 30
⇒ y = 10

Bây giờ người ta hiểu rằng để giải phương trình tuyến tính hai biến, hai phương trình phải được biết và sau đó có thể sử dụng phương pháp thay thế. Hãy hiểu điều này với một vài câu hỏi ví dụ.
Giải pháp độc đáo
Đối với phương trình tuyến tính đã cho có hai biến, nghiệm sẽ là duy nhất cho cả hai phương trình, nếu và chỉ khi chúng cắt nhau tại một điểm duy nhất.
Điều kiện để có nghiệm duy nhất của phương trình tuyến tính đã cho là hệ số góc của đường thẳng tạo bởi hai phương trình tương ứng không bằng nhau.
Xét, m 1 và m 2 là hai phương trình dốc của hai đường thẳng hai biến. Vì vậy, nếu phương trình có nghiệm duy nhất, thì:
m 1 ≠ m 2
Không có giải pháp
Nếu hai phương trình tuyến tính có giá trị hệ số góc bằng nhau thì phương trình đó sẽ không có nghiệm.
m 1 = m 2
Điều này là do các đường thẳng song song với nhau và không cắt nhau.
Hệ phương trình tuyến tính trong hai biến
Thay vì tìm nghiệm của một phương trình tuyến tính có hai biến, chúng ta có thể lấy hai bộ phương trình tuyến tính, cả hai đều có hai biến trong chúng và tìm nghiệm. Vì vậy, về cơ bản hệ phương trình tuyến tính được xác định khi có nhiều hơn một phương trình tuyến tính.
Ví dụ, a + b = 15 và ab = 5, là hệ phương trình tuyến tính hai biến. Bởi vì, điểm a = 10 và b = 5 là nghiệm của cả hai phương trình, chẳng hạn như:
a + b = 10 + 5 = 15
ab = 10-5 = 5
Do đó, điểm đã chứng minh (10,5) là nghiệm cho cả a + b = 15 và ab = 5.
Các vấn đề và giải pháp
Câu hỏi: Tìm giá trị của các biến thỏa mãn phương trình sau:
2x + 5y = 20 và 3x + 6y = 12.
Giải pháp:
Sử dụng phương pháp thay thế để giải cặp phương trình tuyến tính, ta có:
2x + 5y = 20 ……………………. (I)
3x + 6y = 12 …………………… .. (ii)
Nhân phương trình (i) với 3 và (ii) với 2, ta có:
6x + 15y = 60 ……………………. (Iii)
6x + 12y = 24 …………………… .. (iv)
Trừ phương trình (iv) khỏi (iii)
3y = 36
⇒ y = 12
Thay giá trị của y vào bất kỳ phương trình nào (i) hoặc (ii), chúng ta có
2x + 5 (12) = 20
⇒ x = −20
Do đó, x = -20 và y = 12 là giao điểm của phương trình đã cho.
Bây giờ, điều quan trọng là phải biết các ví dụ tình huống còn được gọi là các bài toán từ từ phương trình tuyến tính trong 2 biến.
Các vấn đề từ ngữ
Câu 1: Một chiếc thuyền chạy xuôi dòng quãng đường 20 km trong 2 giờ, ngược dòng quãng đường như vậy mất 5 giờ. Vận tốc của thuyền trong nước yên là bao nhiêu?
Giải pháp:
Những loại câu hỏi này là ví dụ thời gian thực của phương trình tuyến tính trong hai biến số.
Trong nước, hướng dọc theo dòng suối được gọi là hạ lưu. Và, hướng ngược lại dòng suối được gọi là ngược dòng.
Coi vận tốc của thuyền là u km / h và vận tốc của dòng là v km / h thì:
Tốc độ Xuống dòng = (u + v) km / h
Tốc độ Ngược dòng = (u – v) km / h
Chúng tôi biết rằng, Tốc độ = Khoảng cách / Thời gian
Vậy vận tốc của ca nô khi xuôi dòng = (20⁄2) km / h = 10 km / h
Vận tốc của ca nô khi chạy ngược dòng = (20⁄5) km / h = 4 km / h
Từ phía trên, u + v = 10> ……. (1)
u – v = 4 ………. (2)
Thêm phương trình 1 và 2, ta được: 2u = 1
u = 7 km / h
Ngoài ra, v = 3 km / h
Do đó, vận tốc của thuyền trong nước yên = u = 7 km / h
Câu 2: Một chiếc thuyền chạy ngược dòng mất 6 giờ 30 phút để đi hết một quãng đường nhất định, còn thuyền chạy xuôi dòng mất 3 giờ. Tỉ số giữa vận tốc của ca nô và vận tốc của dòng nước lần lượt là?
Giải: Nếu vận tốc xuôi dòng là km / giờ và vận tốc ngược dòng là b km / giờ thì
Tốc độ trong nước tĩnh = (a + b) / 2 km / h
Tốc độ dòng = ½ (a – b) kmph
Cho tốc độ của Thuyền ngược dòng là x kmph và tốc độ xuôi dòng là y kmph.
Sau đó, khoảng cách đi ngược dòng trong 6 giờ 30 phút = Khoảng cách đi xuống hạ lưu trong 3 giờ.
⇒ x × 6,5 giờ = y × 3 giờ
⇒ 13 / 2x = 3y
⇒ y = 13x / 6
Tỷ lệ bắt buộc là = Y+ x2 : Y– x2 ⇒ 13 x6 + x 2 : 13 x6 – x 2 ⇒ 19 x62 : 7 x62
= 19: 7