Tam giác 30-60-90 là gì? Hướng dẫn cách giải hay nhất

Bây giờ khi chúng ta đã hoàn thành với tam giác vuông và các tam giác vuông đặc biệt khác, đã đến lúc đi qua tam giác đặc biệt cuối cùng, đó là tam giác 30 ° -60 ° -90 °.

Nó cũng có tầm quan trọng tương đương với tam giác 45 ° -45 ° -90 ° do mối quan hệ của cạnh của nó. Nó có hai góc nhọn và một góc vuông.

Tam giác 30-60-90 là gì?

Tam giác 30-60-90 là một tam giác vuông đặc biệt có các góc là 30º, 60º và 90º. Hình tam giác đặc biệt vì độ dài các cạnh của nó luôn theo tỷ lệ 1: √3: 2.

Bất kỳ tam giác nào có dạng 30-60-90 đều có thể được giải mà không cần áp dụng các phương pháp từng bước dài như Định lý Pitago và các hàm lượng giác.

Cách dễ nhất để nhớ tỷ lệ 1: √3: 2 là ghi nhớ các con số; “1, 2, 3” . Một lưu ý khi sử dụng phép ghi nhớ này là hãy nhớ rằng 3 nằm dưới dấu căn bậc hai.

Từ hình minh họa trên, chúng ta có thể đưa ra các nhận xét sau về tam giác 30-60-90:

• Chân ngắn hơn, đối diện với góc 30- độ được đánh dấu là x.
• Cạnh huyền, đối diện với góc 90 độ, có chiều dài gấp đôi chiều dài của chân ngắn hơn (2x).
• Chân dài hơn, đối diện với góc 60 độ, bằng tích của chân ngắn hơn và căn bậc hai của ba (x√3).

• 

  Tam giác 30-60-90 là gì?

Làm thế nào để giải quyết một tam giác 30-60-90?

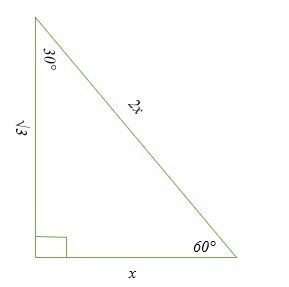
Giải các bài toán liên quan đến 30-60-90 tam giác, bạn luôn biết một cạnh, từ đó bạn có thể xác định các cạnh còn lại. Đối với điều đó, bạn có thể nhân hoặc chia cạnh đó với một hệ số thích hợp.

Bạn có thể tóm tắt các tình huống khác nhau như sau:

• Khi biết cạnh ngắn hơn, bạn có thể tìm cạnh dài hơn bằng cách nhân cạnh ngắn hơn với căn bậc hai của 3. Sau đó, bạn có thể áp dụng Định lý Pitago để tìm cạnh huyền.
• Khi biết cạnh dài hơn, bạn có thể tìm cạnh ngắn hơn bằng cách lặn cạnh dài hơn với căn bậc hai của 3. Sau đó, bạn có thể áp dụng Định lý Pitago để tìm cạnh huyền.
• Khi biết cạnh ngắn hơn, bạn có thể tìm cạnh huyền bằng cách nhân cạnh ngắn hơn với 2. Sau đó, bạn có thể áp dụng Định lý Pitago để tìm cạnh dài hơn.
• Khi cạnh huyền đã biết, bạn có thể tìm cạnh ngắn hơn bằng cách chia cạnh huyền cho 2. Sau đó, bạn có thể áp dụng Định lý Pitago để tìm cạnh dài hơn.

Điều này có nghĩa là cạnh ngắn hơn hoạt động như một cửa ngõ giữa hai cạnh còn lại của một tam giác vuông . Bạn có thể tìm cạnh dài hơn khi cho cạnh huyền hoặc ngược lại, nhưng bạn luôn phải tìm cạnh ngắn hơn trước.

Ngoài ra, để giải các bài toán liên quan đến 30-60-90 tam giác , bạn cần phải biết các tính chất sau của tam giác:

• Tổng các góc nội thất trong bất kỳ tam giác nào, cộng với 180º. Do đó, nếu biết số đo của hai góc, bạn có thể dễ dàng xác định được góc thứ ba bằng cách lấy số đo của hai góc trừ đi 180 độ.
• Cạnh ngắn nhất và cạnh dài nhất trong bất kỳ tam giác nào luôn đối diện với góc nhỏ nhất và góc lớn nhất tương ứng. Quy tắc này cũng áp dụng cho tam giác 30-60-90.
• Các tam giác có cùng số đo góc thì đồng dạng và các cạnh của chúng sẽ luôn có cùng tỉ số với nhau. Do đó, khái niệm đồng dạng có thể được sử dụng để giải các bài toán liên quan đến các hình tam giác 30-60-90.
• Vì tam giác 30-60-90 là tam giác vuông nên định lý Pitago a ²+ b ² = c ² cũng có thể áp dụng được cho tam giác. Ví dụ, chúng ta có thể chứng minh cạnh huyền của tam giác là 2x như sau:

⇒ c ² = x ² + (x√3) ²

⇒ c ² = x ² + (x√3) (x√3)

⇒ c ² = x ² + 3x ²

⇒ c ² = 4x ²

Tìm căn bậc hai của cả hai cạnh.

√c ² = √4x ²

c = 2x

Do đó, đã chứng minh.

Chúng ta hãy làm việc thông qua một số vấn đề thực hành.

Xem thêm:

3 4 5 Hình tam giác vuông là gì và cách giải chi tiết nhất

Tam giác 45 ° -45 ° -90 ° là gì? Hướng dẫn cách giải đơn giản nhất

ví dụ 1

Một tam giác vuông có một góc 60 độ có cạnh dài hơn 8√3 cm. Tính độ dài cạnh ngắn hơn của nó và cạnh huyền.

Giải pháp

Từ tỷ lệ x: x√3: 2x, cạnh dài hơn là x√3. Vì vậy chúng tôi có;

x√3 = 8√3 cm

Bình phương cả hai vế của phương trình.

⇒ (x√3) ² = (8√3) ²

⇒ 3x ² = 64 * 3

⇒ x ² = 64

Tìm bình phương của cả hai cạnh.

√x ² = √64

x = 8 cm

Người thay thế.

2x = 2 * 8 = 16 cm.

Do đó, cạnh ngắn hơn là 8 cm và cạnh huyền là 16 cm.

Ví dụ 2

Thang dựa vào tường tạo với mặt đất một góc 30 độ. Nếu chiều dài của cái thang là 9 m, hãy tìm;

1. Chiều cao của bức tường.
2. Tính độ dài giữa chân thang và tường.

Giải pháp

Cho rằng, một góc là 30 độ, thì đây phải là một tam giác vuông 60 ° – 60 ° – 90 °.

Tỉ lệ = x: x√3: 2x.

⇒ 2x = 9

⇒ x = 9/2

= 4,5

Người thay thế.

1. Chiều cao của bức tường = 4,5 m
2. x√3 = 4,5√3 m

Ví dụ 3

Đường chéo của một tam giác vuông là 8 cm, tìm độ dài hai cạnh còn lại của tam giác cho biết một trong các góc của nó là 30 độ.

Giải pháp

Đây phải là một tam giác 30 ° -60 ° -90 °. Do đó, ta sử dụng tỷ lệ x: x√3: 2x.

Đường chéo = cạnh huyền = 8cm.

⇒2x = 8 cm

⇒ x = 4cm

Người thay thế.

x√3 = 4√3 cm

Cạnh ngắn hơn của tam giác vuông là 4cm và cạnh dài hơn là 4√3 cm.

Ví dụ 4

Tìm giá trị của x và z trong sơ đồ dưới đây:

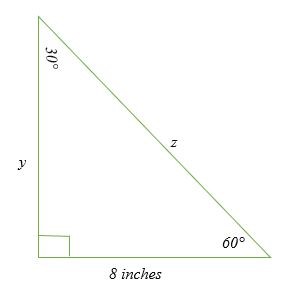
Giải pháp

Chiều dài đo được 8 inch sẽ là chân ngắn hơn vì nó đối diện với góc 30 độ. Để tìm giá trị của z (cạnh huyền) và y (chân dài hơn), chúng ta tiến hành như sau;

Từ tỉ số x: x√3: 2x;

x = 8 inch.

Người thay thế.

⇒ x√3 = 8√3

⇒2x = 2 (8) = 16.

Do đó, y = 8√3 inch và z = 16 inch.

Ví dụ 5

Nếu một góc của tam giác vuông là 30º và số đo của cạnh ngắn nhất là 7 m thì số đo của hai cạnh còn lại là bao nhiêu?

Giải pháp

Đây là hình tam giác 30-60-90 trong đó độ dài các cạnh theo tỷ lệ x: x√3: 2x.

Thay x = 7m cho chân dài hơn và cạnh huyền.

⇒ x √3 = 7√3

⇒ 2x = 2 (7) = 14

Do đó, các cạnh còn lại là 14m và 7√3m

Ví dụ 6 

Trong một tam giác vuông, cạnh huyền là 12 cm và góc nhỏ hơn là 30 độ. Tìm độ dài của chân dài và chân ngắn.

Giải pháp

Cho tỉ số các cạnh = x: x√3: 2x.

2x = 12 cm

x = 6cm

Thay x = 6 cm cho chân dài và chân ngắn;

Chân ngắn = 6cm.

chân dài = 6√3 cm

Ví dụ 7

Hai cạnh của một tam giác là 5√3 mm và 5mm. Tìm độ dài đường chéo của nó.

Giải pháp

Kiểm tra tỷ lệ độ dài các cạnh nếu nó phù hợp với tỷ lệ x: x√3: 2x.

5: 5√3:? = 1 (5): √3 (5):?

Do đó, x = 5

Nhân 2 với 5.

2x = 2 * 5 = 10

Do đó, cạnh huyền bằng 10 mm.

Ví dụ 8

Một đoạn đường dốc tạo với mặt đất một góc 30 độ được sử dụng để hạ tải một xe tải cao 2 feet. Tính độ dài của đoạn đường nối.

Giải pháp

Đây phải là hình tam giác 30-60-90.

x = 2 feet.

2x = 4 bộ

Do đó, chiều dài của đoạn đường nối là 4 feet.

Ví dụ 9

Tìm cạnh huyền của một tam giác 30 ° – 60 ° – 90 ° có cạnh dài hơn là 6 inch.

Giải pháp

Tỉ lệ = x: x√3: 2x.

⇒ x√3 = 6 inch.

Hình vuông cả hai bên

⇒ (x√3) ² = 36

⇒ 3x ² = 36

x ² = 12

x = 2√3 inch.

Ví dụ 10:

Độ dài cạnh huyền của một tam giác vuông với hai cạnh của nó là 4 inch và 4√3 inch.

Giải pháp:

Kiểm tra xem tỷ lệ độ dài có phù hợp với tỷ lệ n: n√3: 2n hay không

4: 4√3:? = n: n√3: 2n

Đúng, đây là tam giác 30-60-90 với n = 4

Bây giờ, hãy tìm chiều dài của cạnh thứ ba.

2n = 2 × 4 = 8

Do đó, chiều dài của cạnh huyền là 8 inch.

Ví dụ 11:

Cạnh huyền và một góc của tam giác vuông là 8 inch và 30 °. tương ứng. Tìm độ dài hai cạnh còn lại của tam giác.
Giải pháp:

Cho rằng tỷ lệ các cạnh là n: n√3: 2n,

Chúng tôi thay thế các giá trị để nhận được,

2n = 8 ⇒ n = 4.
Độ dài của hai cạnh là 4 inch và 4√3 inch.

Vấn đề thực hành

1. Trong một tam giác 30 ° – 60 ° – 90 °, cho cạnh đối diện với góc 60 ° là 9√3. Tìm độ dài của hai cạnh còn lại.
2. Nếu cạnh huyền của tam giác 30 ° – 60 ° – 90 ° là 26, hãy tìm hai cạnh còn lại.
3. Nếu cạnh dài hơn của một tam giác 30 ° – 60 ° – 90 ° là 12 thì tổng hai cạnh còn lại của tam giác này là bao nhiêu?
4. Chứng tỏ rằng, độ dài của một tam giác 30 ° – 60 ° – 90 ° theo tỷ lệ n: n√3: 2n,
5. Tìm chiều dài của biển báo có dạng tam giác đều có chiều cao 18√3 inch.