Cách nhận ra tam thức vuông hoàn hảo siêu nhanh

Tam thức vuông hoàn hảo – Giải thích & Ví dụ

Phương trình bậc hai là một đa thức bậc hai thường ở dạng f (x) = ax ² + bx + c trong đó a, b, c, ∈ R và a ≠ 0. Thuật ngữ ‘a’ được gọi là bậc nhất hệ số, trong khi ‘c’ được gọi là số hạng tuyệt đối của f (x).

Mọi phương trình bậc hai đều có hai giá trị của biến số chưa biết thường được gọi là nghiệm nguyên của phương trình (α, β). Các nghiệm nguyên của phương trình bậc hai có thể thu được bằng cách tính thừa số của phương trình.

Một tam thức vuông hoàn hảo là gì?

Khả năng nhận ra các trường hợp đặc biệt của đa thức có thể dễ dàng tính nhân tử là một kỹ năng cơ bản để giải bất kỳ biểu thức đại số nào có liên quan đến đa thức.

Một trong những đa thức “ dễ nhân tử ” này là tam thức bình phương hoàn hảo. Chúng ta có thể nhớ rằng một tam thức là một biểu thức đại số bao gồm ba số hạng được nối với nhau bằng phép cộng hoặc phép trừ.

Tương tự, một nhị thức là một biểu thức bao gồm hai số hạng . Do đó, một tam thức bình phương hoàn hảo có thể được định nghĩa là một biểu thức nhận được bằng cách bình phương một nhị thức

Học cách nhận ra một tam thức vuông hoàn hảo là bước đầu tiên để tính toán nó.

Sau đây là các mẹo về cách nhận ra một tam thức vuông hoàn hảo:

• Kiểm tra xem số hạng đầu tiên và số hạng cuối cùng của tam thức có phải là hình vuông hoàn hảo hay không
• Nhân các gốc của số hạng thứ nhất và thứ ba với nhau.
• So sánh với các điều khoản ở giữa với kết quả ở bước hai
• Nếu số hạng đầu tiên và số hạng cuối là bình phương hoàn hảo, và hệ số của số hạng giữa gấp đôi tích của căn bậc hai của số hạng đầu và số hạng cuối, thì biểu thức là một tam thức bậc hai.

Làm thế nào để thừa số một tam thức vuông hoàn hảo?

Khi bạn đã xác định được một tam thức bình phương hoàn hảo, việc tính thừa số nó là một quá trình khá đơn giản.

Chúng ta hãy xem xét các bước để tính một tam thức vuông hoàn hảo.

• Xác định các số bình phương trong số hạng đầu tiên và số hạng thứ ba của tam thức
• Kiểm tra kỳ hạn giữa nếu nó có kết quả tích cực hoặc tiêu cực. Nếu số hạng giữa của tam thức là số dương hoặc số âm thì các thừa số sẽ có dấu cộng và dấu trừ tương ứng.
• Viết ra các điều khoản của bạn bằng cách áp dụng các đặc điểm sau:

(i) a ²  + 2ab + b ²  = (a + b) ²  = (a + b) (a + b)
(ii) a ²  – 2ab + b ²  = (a – b) ²  = (a – b ) (a – b)

Công thức tam thức bình phương hoàn hảo

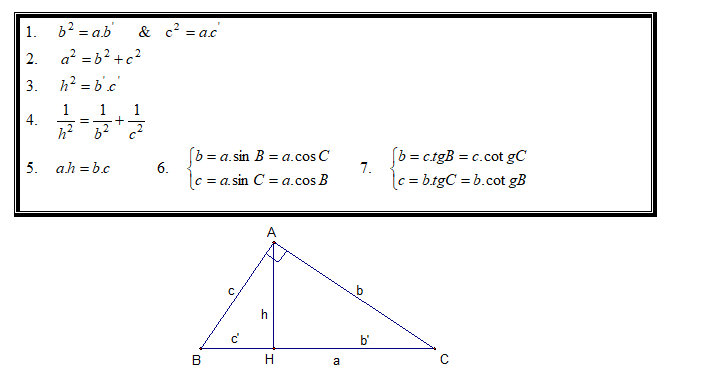
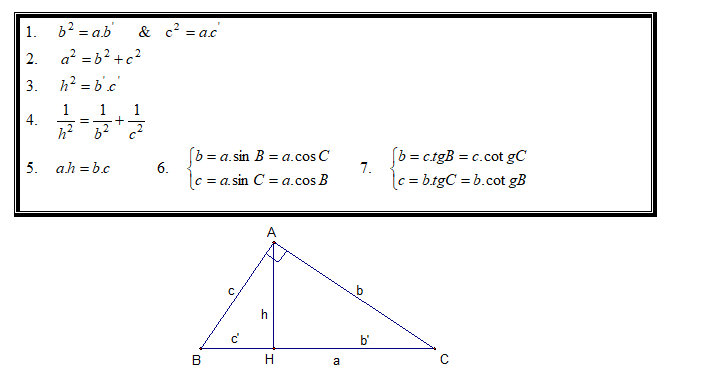
Một biểu thức thu được từ bình phương của phương trình nhị thức là một tam thức bình phương hoàn hảo. Một biểu thức được cho là một tam thức vuông hoàn hảo nếu nó có dạng ax ²  + bx + c và thỏa mãn điều kiện b ²  = 4ac.

Công thức bình phương hoàn hảo có các dạng sau:

• (ax) ²+ 2abx + b ² = (ax + b) ²
• (ax) ²−2abx + b ² = (ax − b) ²

ví dụ 1

Hệ số x ² + 6x + 9

Giải pháp

Ta có thể viết lại biểu thức x ²  + 6x + 9 dưới dạng a ²  + 2ab + b ² là;
x ² + 6x + 9 ⟹ (x) ²  + 2 (x) (3) + (3) ²
Áp dụng công thức a ²  + 2ab + b ²  = (a + b) ²  vào biểu thức;
= (x + 3) ²
= (x + 3) (x + 3)

Ví dụ 2

Hệ số x ²  + 8x + 16

Giải pháp

Viết biểu thức x ²  + 8x + 16 dưới dạng a ²  + 2ab + b ²

x ²  + 8x + 16 ⟹ (x) ²  + 2 (x) (4) + (4) ²
Bây giờ chúng ta sẽ áp dụng công thức tam thức vuông hoàn hảo;

= (x + 4) ²
= (x + 4) (x + 4)

Ví dụ 3

Hệ số 4a ²  – 4ab + b ²

Giải pháp

4a ²  – 4ab + b ² ⟹ (2a) ²  – (2) (2) ab + b ²

= (2a – b) ²

= (2a – b) (2a – b)

Ví dụ 4

Hệ số 1- 2xy- (x ²  + y ² )

Giải pháp

1- 2xy- (x ²  + y ² )
= 1 – 2xy – x ²  – y ²
= 1 – (x ²  + 2xy + y ² )
= 1 – (x + y) ²
= (1) ²  – (x + y) ²

= [1 + (x + y)] [1 – (x + y)]

= [1 + x + y] [1 – x – y]

Ví dụ 5

Hệ số 25y ²  – 10y + 1

Giải pháp

25y ²  – 10y + 1⟹ (5y) ²  – (2) (5) (y) (1) + 1 ²

= (5y – 1) ²

= (5y– 1) (5y – 1)

Ví dụ 6

Hệ số 25t ²  + 5t / 2 + 1/16.

Giải pháp

25t ²  + 5t / 2 + 1/16 ⟹ (5t) ² + (2) (5) (t) (1/4) + (1/4) ²

= (5t + 1/4) ²

= (5t + 1/4) (5t + 1/4)

Ví dụ 7

Thừa số x ⁴  – 10x ² y ² + 25y ⁴

Giải pháp

x ⁴ – 10x ² y ²  + 25y ⁴ ⟹ (x ² ) ²  – 2 (x ² ) (5y ² ) + (5y ² ) ²

Áp dụng công thức a ²  + 2ab + b ²  = (a + b) ²  để được,
= (x ²  – 5y ² ) ²
= (x ²  – 5y ² ) (x ²  – 5y ² )

Xem thêm:

Cách để hoàn thành bình phương nhanh nhất hiện nay

Sự khác biệt của các hình vuông – Cách giải quyết nhanh nhất

Câu hỏi thực hành

Nhân tử của các tam thức bình phương hoàn hảo sau:

1. x ²  + 12x + 36
2. 9a ²  – 6a + 1
3. (m + n) ²  + 12 (m + n) + 36
4. x ²  + 4x + 4
5. x ² + 2x + 1
6. x ² + 10x + 25
7. 16x ² – 48x + 36
8. x ²  + x + ¼
9. Z ² + 1 / z ² – 2.
10. 4x ² – 20x + 25

Câu trả lời

1. (x + 6) (x + 6)
2. (3a – 1) (3a – 1)
3. (m + n + 6) (m + n + 6)
4. (x + 2) (x + 2)
5. (x + 1) (x + 1)
6. (x + 5) (x + 5)
7. (4x– 6) (4x – 6)
8. (x + 1/2) (x + 1/2)
9. (z – 1 / z ² ) (z – 1 / z ² )
10. (2x – 5) (2x – 5)