|
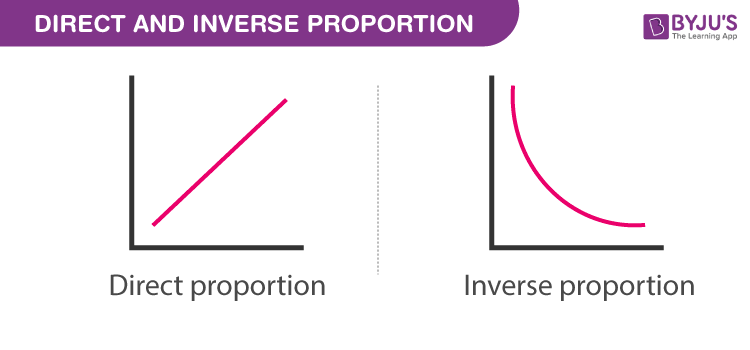
Định nghĩa tỷ lệ nghịch và trực tiếp
Tỷ lệ được cho là tỷ lệ trực tiếp giữa hai giá trị khi một giá trị là bội số của giá trị kia.
Ví dụ, 1 cm tương đương với 10 mm.
Ở đây, để chuyển đổi cm sang mm, hệ số nhân phải là 10.

Tỷ lệ trực tiếp
Hai đại lượng a và b được cho là tỉ lệ thuận nếu chúng tăng hoặc giảm cùng nhau. Nói cách khác, tỷ lệ các giá trị tương ứng của chúng không đổi. Điều này có nghĩa rằng,
a / b = k
với k là một số dương, thì các đại lượng a và b được cho là biến thiên trực tiếp.
Trong trường hợp đó nếu các giá trị b 1 , b 2 của b tương ứng với các giá trị a 1 , a 2 của a thì nó trở thành;
a 1 / / b 1 = a 2 / b 2
Tỷ trọng trực tiếp còn được gọi là biến thiên trực tiếp .
Biểu tượng tỷ lệ trực tiếp
Ký hiệu được sử dụng để biểu thị tỷ lệ trực tiếp là “ ∝” .
Hãy xem xét tuyên bố,
a tỷ lệ thuận với b
Điều này có thể được viết bằng cách sử dụng ký hiệu là:
a ∝ b
Hãy xem xét câu lệnh khác, a = 2b
Trong trường hợp này, nó cho thấy rằng a tỷ lệ với b và giá trị của một biến có thể được tìm thấy nếu giá trị của biến khác được cho.
Ví dụ:
Cho b = 7
Do đó, a = 2 x 7 = 14
Tương tự, nếu bạn lấy giá trị của “a” là 14, bạn sẽ tìm thấy giá trị của b
Như vậy mà
14 = 2 xb
14/2 = b
Do đó, b = 7
Tỷ lệ ngược
Giá trị được cho là tỷ lệ nghịch khi một giá trị tăng và giá trị kia giảm. Biểu tượng tỷ lệ được sử dụng theo một cách khác. Hãy xem xét một ví dụ; chúng tôi biết rằng càng nhiều công nhân trong một công việc sẽ làm giảm thời gian hoàn thành nhiệm vụ. Nó được đại diện là
Số lượng công nhân ∝ (1 / Thời gian hoàn thành công việc)
Định nghĩa tỷ lệ nghịch
Hai đại lượng a và b tỷ lệ nghịch với nhau, nếu tăng đại lượng a thì đại lượng b giảm và ngược lại. Nói cách khác, tích của các giá trị tương ứng của chúng phải không đổi. Đôi khi, nó còn được gọi là biến thể nghịch đảo
Nghĩa là, nếu ab = k, thì a và b được cho là biến thiên nghịch biến. Trong trường hợp này, nếu b 1 , b 2 lần lượt là giá trị của b tương ứng với các giá trị a 1 , a 2 của a thì a 1 b 1 = a 2 b 2 hoặc a 1 / a 2 = b 2 / b 1
Câu lệnh ‘a tỉ lệ nghịch với b được viết dưới dạng
a ∝ 1 / b
Ở đây, một phương trình được đưa ra liên quan đến tỷ lệ nghịch có thể được sử dụng để tính các giá trị khác.
Để cho,
a = 25 / b
Ở đây a tỷ lệ nghịch với b
Nếu một giá trị được cho, giá trị khác có thể dễ dàng tìm thấy.
Nói b = 10
a = 25/10 = 2,5
Tương tự, nếu a = 2,5, giá trị của b có thể nhận được.
2,5 = 25 / b
b = 25 / 2,5 = 10
Làm thế nào để thiết lập một phương trình?
- Đầu tiên, hãy viết ra ký hiệu tỷ lệ.
- Chuyển nó thành một phương trình sử dụng hằng số tỷ lệ.
- Tìm hằng số tỉ lệ từ thông tin đã cho.
- Sau khi tìm được hằng số tỉ lệ, hãy thay thế vào một phương trình.
Ví dụ về tỷ lệ nghịch và trực tiếp
Dưới đây là các ví dụ để hiểu rõ hơn về khái niệm tỷ lệ nghịch và tỷ lệ nghịch.
Ví dụ 1:
Một đoàn tàu đang chuyển động với vận tốc đều 75 km / giờ.
(i) Xe lửa đi được bao nhiêu km trong 20 phút?
(ii) Tìm thời gian cần thiết để đi được quãng đường 250 km.
Giải pháp:
Gọi quãng đường đi được (tính bằng km) trong 20 phút là a và thời gian đi (tính bằng phút) để đi hết quãng đường 250 km là b.
| Khoảng cách đã đi (tính bằng km) | 75 | a | 250 |
| Thời gian thực hiện (tính bằng phút) | 60 | 20 | b |
Chúng tôi biết rằng 1 giờ = 60 phút
Vì tốc độ của tàu là đều, do đó, quãng đường đi được sẽ tỷ lệ thuận với thời gian.
(i) Ta có 75/60 = a / 20
hoặc (75/60) 20 = a
hoặc a = 25
Vì vậy, đoàn tàu sẽ đi quãng đường 25 km trong 20 phút.
(ii) Ngoài ra, 75/60 = 250 / b hoặc
b = (250 x 60) / 75
b = 200 phút hoặc 3 giờ 20 phút.
Do đó, cần 3 giờ 20 phút để đi hết quãng đường 250 km.
Ngoài ra, khi biết a, thì người ta có thể xác định b, sử dụng quan hệ
a / 20 = 250 / b
Ví dụ 2:
Giá trị f tỷ lệ thuận với g. Khi f = 20 thì g = 10. Tìm phương trình liên hệ giữa f và g.
Giải pháp:
Cho trước, f ∝ g
hoặc chúng ta có thể viết,
f = kg, trong đó k là tỷ lệ không đổi.
20 = kx 10
k = 2
Do đó, phương trình yêu cầu là;
f = 2g
Xem thêm: