- Về mặt hình học
- Về mặt đại số


Sản phẩm chấm – Định nghĩa hình học
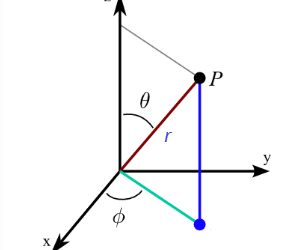
Tích số chấm của vectơ được viết dưới dạng ab = | a || b | cosϴ
Ở đâu | a | và | b | là độ lớn của vectơ a và b và ϴ là góc giữa vectơ a và b.
Nếu hai vectơ là trực giao, tức là, góc giữa chúng là 90 thì ab = 0 vì cos 90 là 0.
Nếu hai vectơ song song với nhau thì ab = | a || b | như cos 0 là 1.
Sản phẩm chấm – Định nghĩa đại số
Tích số chấm của Vectơ được viết là
Tích chấm của vector – Một ví dụ
Cho có hai vectơ [6,2, -1] và [5, -8,2]
ab = (6) (5) + (2) (- 8) + (- 1) (2)
ab = 30-16-2
ab = 12
Cho có hai vectơ | a | = 4 và | b | = 2 và ϴ = 60
ab = | a || b | cos 60
ab = 4,2cos60
ab = 4
Sản phẩm chấm của Vector – Thuộc tính
Sau đây là các thuộc tính Vector:
Tính chất giao hoán
ab = ba
ab = | a || b | cosϴ
ab = | b || a | cosϴ
Thuộc tính phân tán
a. (b + c) = a.b + ac
Bất động sản Bilinear
a. (rb + c) = r. (ab) + (ac)
Thuộc tính Nhân vô hướng
(xa). (yb) = xy (ab)
Thuộc tính không liên kết
Bởi vì một tích số chấm giữa một đại lượng vô hướng và một vectơ không được phép
Thuộc tính trực giao
Hai vectơ chỉ trực giao với nhau khi ab = 0
Sản phẩm chấm của Vector – Hàm có giá trị
Tích số chấm của các hàm có giá trị vectơ, r (t) và u (t), mỗi hàm cung cấp cho bạn một vectơ tại mỗi “thời điểm” t cụ thể, và do đó hàm r (t) ⋅u (t) là một hàm vô hướng.
Suy ra, tích chấm tại mỗi t cho trước; sản phẩm này đo lường chính xác mối quan hệ giữa r (t) và u (t)
Xem thêm: