các quy luật của số mũ, xem xong hiểu luôn.

các quy luật của số mũ

Bạn có đọc được 10.000.000.000.000.000.000.000.000.000 không? Con số tự nhiên khổng lồ  này không dễ đọc, nhìn nhận và đánh giá. Số mũ giúp dễ dàng đọc, nhận biết và đánh giá các số rất lớn. Số mũ còn được gọi là lũy thừa hoặc chỉ số. Số mũ có nghĩa là gì? Luật số mũ là gì? Làm thế nào để áp dụng luật số mũ để đơn giản hóa các biểu thức? Chúng ta hãy cùng tìm hiểu tổng quan về luật số mũ.

Quy tắc số mũ với ví dụ

Số mũ được định nghĩa là một số cho biết chúng ta phải nhân với số cơ sở bao nhiêu lần. Nó được viết phía trên bên phải của số cơ sở.

1. 5 ²= “5 được nâng lên lũy thừa của 2” hoặc “5 bình phương.”
2. 5 ³= “5 được nâng lên lũy thừa của 3” hoặc “10 khối.”

Ví dụ 1: 10.000 = 10 x 10 x 10 x 10 = 10 ⁴

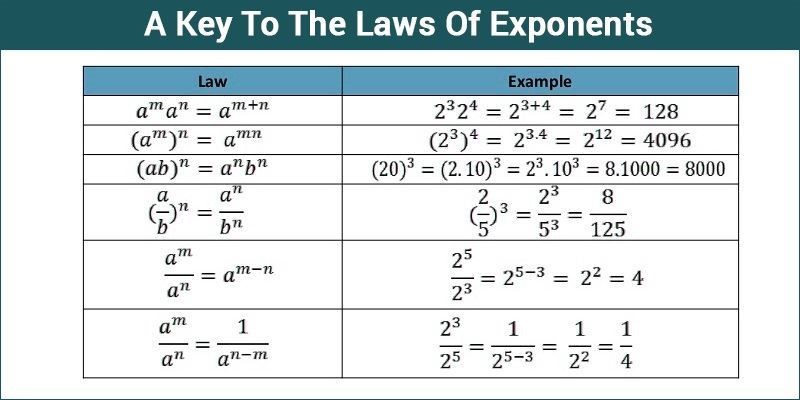
Luật lũy thừa nêu các quy tắc sau đây để đơn giản hóa các biểu thức. Một số trong số chúng như sau:

Quy tắc 1: Khi các số có cùng cơ số được nhân lên, hãy cộng các số mũ.

a ^p × a ^q = a ^{(p + q)}

a = cơ số: p, q = số mũ

Ví dụ 1: Hãy để chúng tôi tính toán,

3 ² × 3 ⁴

Giải pháp:

3 ² × 3 ⁴ = 3 ^{{(2 + 4)}} = 3 ⁶

Trong ví dụ trên, các số cơ sở giống nhau. (tức là,) 3 ² và 3 ⁴ . Tổng của các lũy thừa là 6.

Quy tắc 2: Khi các số có cùng cơ số bị chia, trừ các số mũ.

a ^p ÷ a ^q = a ^{(pq)} tức là a = cơ số: p, q = số mũ

Ví dụ 2: 3 ⁴ ÷ 3 ² =?

Giải pháp:

3 ⁴ ÷ 3 ² = 3 ^{(4-2)} = 3 ²

Trong ví dụ trên, các cơ sở giống nhau. (tức là, 3 ⁴ và 3 ² ).

Quy tắc 3: Nhân các lũy thừa khi các số đó được nâng lên với một số khác.

(a ^p ) ^q = a ^{(pxq)} = a ^{(pq)}

Ví dụ 3: (2 ³ ) ² =?

Giải: (2 ³ ) ² = 2 ^{{(3 × 2)}} = 2 ⁶

Các vấn đề ví dụ

Ví dụ 1:

Nhân các lũy thừa với cùng một cơ số

3 ² × 3 ³ =?

Giải pháp:

Trong ví dụ trên, theo quy tắc 1, hãy cộng lũy ​​thừa khi các số được nhân lên.

Vì thế,

3 ² × 3 ³ = 3 ^{{(2 + 3)}} = 3 ⁵

Ví dụ 2:

Phân chia lũy thừa cùng cơ số

4 ⁵ ÷ 4 ²

Giải pháp:

Trong ví dụ trên, theo quy tắc 2, trừ lũy thừa khi các số bị chia.

Vì thế,

4 ⁵ ÷ 4 ² = 4 ^{(5-2)} = 4 ³

Như vậy, chúng ta đã xem phần giới thiệu cơ bản này và các ví dụ về luật số mũ.

Xem thêm: 

• Tỷ lệ nghịch là gì? xem xong 5 phút hiểu luôn.
• Quy tắc bệnh viện L là gì? Xem xong 5 phút hiểu luôn.

  Tích phân là gì? Xem xong 5 phút hiểu luôn.