Các thông tin cần biết về công thức khoảng cách

Bạn đang tìm hiểu những thông tin liên quan đến công thức khoảng cách, khoảng cách trong không gian, những câu hỏi đặt ra khoảng cách trong không gian là gì và cách tính khoảng cách như thế nào, có các dạng bài toán tính khoảng cách ra làm sao..?

Để giải đáp và làm sáng tỏ các thắc mắc trên hôm nay tintuctuyensinh của chúng tôi sẽ giúp các bạn hệ thống và tổng hợp lại các kiến thức liên quan đến tính khoảng cách trong không gian và hướng dẫn cách giải quyết các dạng bài tập liên quan đến công thức khoảng cách. Từ đó xây dựng cho bạn các phương pháp làm bài tập công thức khoảng cách hiệu quả để đạt thành tích tốt nhất trong các kỳ thi.

1. NHẬN THỨC CHUNG VỀ KHOẢNG CÁCH

Trong kiến thức môn toán học nói chung phần hình học là phần kiến thức trọng tâm và được đánh giá không quá khó để lấy điểm, nhưng phần lớn các bạn học sinh lại rất sợ khi gặp các bài toán liên quan đến hình học không gian đặc biệt các bài toán về tính khoảng cách. Nhưng nếu bạn nắm được bản chất của các dạng bài toán về khoảng cách thì rất dễ để giải quyết vấn đề này.

Đầu tiên bạn cần hiểu rõ khái niệm về khoảng cách trong không gian là gì? Khái niệm về khoảng cách trong không gian được biết đến trong chương trình toán học lớp 11 thì sẽ tính được công thức khoảng cách.

Các bài toán liên quan quan đến khoảng cách được chia thành 3 dạng khác nhau đó là bài toán về tính khoảng cách từ một điểm đến một mặt phẳng, dạng thứ hai là tính khoảng cách từ một đường thẳng đến một mặt phẳng và dạng cuối cùng là tính khoảng cách giữa hai đường thẳng chéo nhau.

Đây là dạng khó nhất trong ba dạng bài toán mà bạn cần giải quyết.

Khái niệm khoảng cách trong không gian là gì?

Khái niệm khoảng cách trong không gian là độ dài đường vuông góc hạ từ điểm đã cho đến mặt phẳng hoặc đường thẳng xác định từ trước. Hay là khoảng cách từ điểm cho trước tới hình chiếu của nó lên đường thẳng hoặc mặt phẳng.

2. CÁC DẠNG BÀI TOÁN VỀ CÔNG THỨC KHOẢNG CÁCH

Dạng công thức khoảng cách 1: Bài toán về tính khoảng cách từ một điểm cho trước đến một mặt phẳng hoặc đến một đường thẳng.

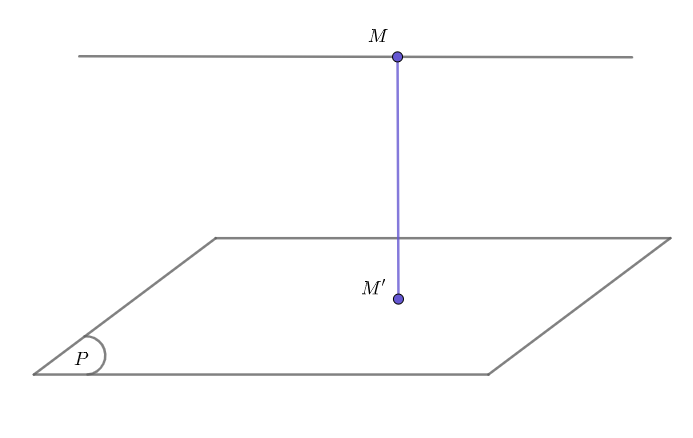
  Bài toán mô tả công thức khoảng cách: Cho đường thẳng d hoặc một mặt phẳng (P) và một điểm M không thuộc đường thẳng d. Yêu cầu tính khoảng cách từ điểm M đến đường thẳng d.

Hướng dẫn: Lấy H là hình chiếu vuông góc của M lên đường thẳng d sao cho MH vuông góc với đường thẳng d.

Khi đó khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên đường thẳng d , kí hiệu là d(M, d) (hoặc trên mặt phẳng (P) kí hiệu d( M,(P))) là khoảng cách cần tìm.

   Dạng công thức khoảng cách 2. Tính khoảng cách giữa đường thẳng và mặt phẳng song song hoặc giữa hai mặt phẳng song song.

Bài toán công thức khoảng cách mô tả:

  Cho đường thẳng a song song với mặt phẳng (P). Yêu cầu tính khoảng cách giữa đường thẳng d và mặt phẳng (P).

Hướng dẫn: khi đó ta chỉ cần lấy một điểm A thuộc đường thẳng a sau đó hạ hình chiếu của A lên mặt phẳng (P) là điểm B. Sao cho AB vuông góc với mặt phẳng (P). Khi đó khoảng cách cần tìm là độ dài AB 

kí hiệu là d(a, (P)).

Dạng công thức khoảng cách 3: Bài toán tính khoảng cách giữa hai mặt phẳng song song.

Cho hai mặt phẳng (P) và (Q) song song với nhau yêu cầu tìm khoảng cách giữa hai mặt phẳng đó

Hướng dẫn công thức khoảng cách:

Tương tự như dạng 2 ta lấy điểm A thuộc mặt phẳng ( P ) sau đó hạ hình chiếu vuông góc của A  lên mặt phẳng (Q) là điểm M sao cho AM vuông góc với mặt phẳng (Q). Khi đó khoảng cách cần tìm là độ dài đoạn thẳng AM.

   Dạng công thức khoảng cách 4 Bài toán tính khoảng cách giữa hai đường thẳng chéo nhau 

   Bài toán mô tả công thức khoảng cách:

Cho hai đường thẳng a và b chéo nhau trong không gian. Yêu cầu tính khoảng cách giữa hai đường thẳng đã cho.

Hướng dẫn công thức khoảng cách:

Cách 1

Kẻ đường thẳng c cắt đồng thời hai đường thẳng a và b sao cho đường thẳng c vuông góc với đường thẳng a và vuông góc với đường thẳng b. Khi đó khoảng cách của hai đường thẳng chéo nhau a và b là khoảng cách đoạn vuông góc chung mà ta vừa vẽ được.

Cách 2

Dựng một mặt phẳng (P) chứa đường thẳng a và song song với đường thẳng b. Khi đó bài toán trở về tính khoảng cách từ 1 đường thẳng đến 1 mặt phẳng. Vì vậy chúng ta chỉ cần lấy một điểm bất kì trên đường thẳng b hạ hình chiếu vuông góc lên mặt phẳng P ta được khoảng cách cần tìm.

Cách 3

Dựng hai mặt phẳng  chứa  hai đường thẳng a và b sao cho hai mặt phẳng này song song với nhau. Khi đó bài toán công thức khoảng cách trở về dạng tính khoảng cách giữa hai mặt phẳng song song mà chúng ta đã được giới thiệu ở phần trên. 

Trên đây là toàn bộ những kiến thức liên quan đến khái niệm khoảng  cách mà tintuctuyensinh của chúng tôi đã cung cấp cho các bạn.

Hy vọng công thức khoảng cách đây là nguồn tài liệu hữu ích cho các bạn tham khảo và tổng hợp, bổ sung nâng cao kiến thức về phần hình học không gian mà bạn đã được học. Từ đó là cơ sở để bạn hoàn thành và giải quyết tốt các bài tập liên quan đến vấn đề công thức khoảng cách này.  

Chúc các bạn sức khỏe và thành công!!!

Xem thêm: 

Bí quyết thêm số mũ hiệu quả nhanh chóng nhất

Phép trừ các số mũ dễ hiểu, giải nhanh nhất 2021

Số mũ là gì? Những thông tin mới nhất về nó