Cách giải phương trình vi phân tuyến tính là gì? Xem xong 5 phút hiểu luôn.

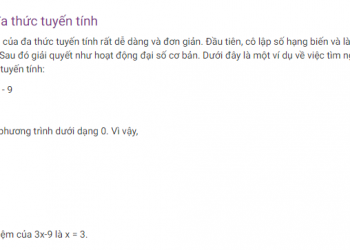
dy / dx + Py = Q trong đó y là hàm và dy / dx là đạo hàm.

Nghiệm của phương trình vi phân tuyến tính tạo ra giá trị của biến y.

Ví dụ:

• dy / dx + 2y = sin x
• dy / dx + y = e ^x

Định nghĩa phương trình vi phân tuyến tính

Phương trình vi phân tuyến tính được xác định bởi phương trình đa thức tuyến tính, bao gồm các đạo hàm của một số biến. Nó cũng được phát biểu là Phương trình vi phân từng phần tuyến tính khi hàm phụ thuộc vào các biến và đạo hàm là từng phần.

Phương trình vi phân có dạng trên được gọi là phương trình vi phân tuyến tính bậc nhất  trong đó P và Q chỉ là hằng số hoặc hàm của biến độc lập (trong trường hợp này là x).

Ngoài ra, phương trình vi phân có dạng,  dy / dx + Py = Q , là   phương trình vi phân tuyến tính cấp một trong đó P và Q chỉ là hằng số hoặc hàm của y (biến độc lập).

Để tìm nghiệm phương trình vi phân tuyến tính, chúng ta phải suy ra dạng tổng quát hoặc biểu diễn của nghiệm.

Phương trình vi phân không tuyến tính

Khi một phương trình không tuyến tính trong hàm chưa biết và các đạo hàm của nó, thì nó được cho là một phương trình vi phân phi tuyến. Nó cung cấp các giải pháp đa dạng có thể được nhìn thấy cho sự hỗn loạn.

Giải phương trình vi phân tuyến tính

Để tìm nghiệm của phương trình vi phân tuyến tính như vậy, chúng ta xác định một hàm của biến độc lập, giả sử M (x), được gọi là hệ số tích phân (IF).

Nhân cả hai vế của phương trình (1) với tích phân số M (x) ta được;

M (x) dy / dx + M (x) Py = QM (x)  … .. (2)

Bây giờ chúng tôi chọn M (x) theo cách sao cho LHS của phương trình (2) trở thành đạo hàm của yM (x)

tức là    d (yM (x)) / dx = (M (x)) dy / dx + y (d (M (x))) dx… (Sử dụng d (uv) / dx = v (du / dx) + u (dv / dx)

⇒ M (x) / (dy / dx) + M (x) Py = M (x) dy / dx + yd (M (x)) / dx

⇒ M (x) Py = y dM (x) / dx

⇒ 1 / M ‘(x) = P.dx 

Tích cả hai vế đối với x, ta được;

log M (x) = ∫Pdx ( A s ∫f′( x )f( x )) = l o gf( x )

⇒ M (x) = e∫Pdx NẾU

Bây giờ, sử dụng giá trị này của hệ số tích phân, chúng ta có thể tìm ra nghiệm của phương trình vi phân tuyến tính bậc nhất.

Nhân cả hai vế của phương trình (1) với IF ta được

e∫PdxdYdx+ vàPe∫Pdx= Qe∫Pdx

Điều này có thể dễ dàng được viết lại thành:

d( và.e∫Pdx)dx= Qe∫Pdx( Us tôi n gd( u v )dx= vdudx+ udvdx)

Bây giờ tích hợp cả hai bên đối với x, chúng ta nhận được:

∫d( và.e∫Pdx) = ∫Qe∫Pdxdx + c

Y=1e∫Pdx( ∫Qe∫Pdxdx + c )

trong đó C là một số hằng số tùy ý.

Cách giải phương trình vi phân tuyến tính bậc nhất

Tìm hiểu cách giải phương trình vi phân bậc nhất với sự trợ giúp của các bước dưới đây.

1. Sắp xếp lại các số hạng của phương trình đã cho dưới dạng dy / dx + Py = Q

trong đó P và Q chỉ là hằng số hoặc hàm của biến độc lập x.

2. Để có thừa số tích phân, tích phân P (thu được ở bước 1) với x và đặt tích phân này dưới dạng lũy ​​thừa của e.

e∫Pdx = NẾU

3. Nhân cả hai vế của phương trình vi phân tuyến tính bậc nhất với IF

e∫PdxdYdx+ vàPe∫Pdx= Qe∫Pdx

4. LHS của phương trình luôn là đạo hàm của y × M (x)

tức là LHS = d (y × IF) / dx

d (y × IF) dx = Q × IF 

5. Trong bước cuối cùng, chúng ta chỉ cần tích hợp cả hai vế đối với x và nhận được số hạng C không đổi để có được nghiệm.

∴ y × IF = ∫Q × I. Fdx + C ,

trong đó C là một số hằng số tùy ý

Tương tự, chúng ta cũng có thể giải một dạng khác của phương trình vi phân tuyến tính bậc nhất dx / dy + Px = Q bằng các bước tương tự. Ở dạng này P và Q là các hàm của y. Yếu tố tích hợp (IF) xuất hiện và sử dụng điều này, chúng tôi tìm ra giải pháp

(x) × (IF) = ∫Q × I. FdY+ c

Bây giờ, để hiểu rõ hơn về phương trình vi phân tuyến tính, chúng ta hãy thử giải một số câu hỏi. trong đó C là một số hằng số tùy ý.

Các ví dụ đã giải quyết

Ví dụ 1: Giải LDE =   dy / dx = [1 / (1 + x ³ )] – [3x ² / (1 + x ² )] y

Giải pháp:

Phương trình đã đề cập ở trên có thể được viết lại thành   dy / dx + [3x ² / (1 + x ² )] y = 1 / (1 + x ³ )

So sánh nó với  dy / dx + Py = O , chúng ta nhận được

P = 3x ² /1 + x ³

Q = 1/1 + x ³

Hãy tìm ra hệ số tích phân (IF) là e∫Pdx

⇒IF =  e∫3x21 +x3dx =el n ( 1 +x3)

⇒IF = 1 + x ³

Bây giờ, chúng ta cũng có thể viết lại LHS thành:

d (y × IF) / dx, 

⇒ d (y × (1 + x ³ )) dx = [1 / (1 + x ³ )] × (1 + x ³ )

Tích hợp cả hai cạnh wrt x, chúng tôi nhận được,

⇒ y ×  (1 + x ³ ) = x

⇒ y = x / (1 + x ³ )

⇒ y = [ x / (1 + x ³  ) + C

Ví dụ 2:

Giải phương trình vi phân sau:  

dy / dx + (giây x) y = 7 

Giải pháp:

So sánh phương trình đã cho với dy / dx + Py = Q 

Ta thấy, P = giây x, Q = 7

Bây giờ chúng ta hãy tìm hiểu hệ số tích phân bằng công thức

e∫Pdx= NẾU

⇒e∫s e c dx  = NẾU

⇒IF =  el n | s e c x + t a n x |= s e c x + t a n x

Bây giờ chúng ta cũng có thể viết lại LHS dưới dạng

d (y × IF) / dx} ,

I E. d (y × (giây x + tan x))

⇒ d (y × (giây x + tan x)) / dx = 7 (giây x + tan x) 

Tích hợp cả hai cạnh wrt x, chúng tôi nhận được,

∫d( và× ( s e c x + t a n x ) ) = ∫7 ( s e c x + t a n x ) dx

⇒ y× ( s e c x + t a n x ) = 7 ( l n | s e c x + t a n x | + l o g| secx | )

⇒ y = 7 ( l n | s e c x + t a n x | + l o g| secx |( s e c x + t a n x )+ c

Ví dụ 3:

Một đường cong đi qua gốc tọa độ và hệ số góc của tiếp tuyến tại điểm R (x, y) trong đó -1 <x <1 là ( x ⁴ + 2xy + 1) / (1 – x ² ) . Phương trình của đường cong sẽ như thế nào?

Giải pháp:

Chúng ta biết rằng hệ số góc của tiếp tuyến tại (x, y) là,

tanƟ = dy / dx = (x ⁴ + 2xy + 1) / 1 – x ²

Sắp xếp lại phương trình ở dạng dy / dx + Py = Q  , chúng ta nhận được

dy / dx = 2xy / (1 – x ² ) + (x ⁴ + 1) / (1 – x ² )

⇒ dy / dx – 2xy / (1 – x ² ) = (x ⁴ + 1) / (1 – x ² )

So sánh ta được P = -2x / (1 – x ² )

Q = ( x ⁴ + 1) / (1 – x ² )

Bây giờ, chúng ta hãy tìm hiểu hệ số tích phân bằng cách sử dụng công thức.

e∫Pdx= NẾU

⇒ e∫– 2 x1 –x2dx =el n ( 1 –x2)= 1 –x2 NẾU

Bây giờ chúng ta cũng có thể viết lại LHS dưới dạng

d( và× tôi. F)dx,

I E d( và× ( 1 –x2) )dx=x4+ 11 –x2× 1 –x2

Tích hợp cả hai cạnh wrt x, chúng tôi nhận được,

∫d( và× ( 1 –x2) ) = ∫x4+ 11 –x2× ( 1 –x2) dx

⇒ y× ( 1 –x2) = ∫x4+ 1 ngàyx   …… (1)

 x (1 – x ² ) = x ⁵ /5 + x + C

⇒ y = x ^5/5 + x / (1 – x ² ) + C 

Nó là phương trình bắt buộc của đường cong. Cũng như đường cong đi qua điểm gốc; thay các giá trị x = 0, y = 0 vào phương trình trên. Như vậy, C = 0.

Do đó, phương trình của đường cong là:  ⇒ y = x ⁵ /5 + x / (1 – x ² )