Cách tính diện tích bề mặt của một hình trụ chưa đầy 1 phút

Trước khi chúng ta đi vào chủ đề về diện tích bề mặt của một hình trụ, chúng ta hãy xem xét về một hình trụ. Trong hình học, hình trụ là một hình ba chiều có hai đáy là hình tròn song song với nhau và một mặt cong.

Làm thế nào để tìm diện tích bề mặt của một hình trụ?

Diện tích bề mặt của hình trụ là tổng của hai mặt tròn song song và đồng dạng và diện tích mặt cong.

Trong bài này, chúng ta sẽ thảo luận về cách tìm tổng diện tích bề mặt và diện tích mặt bên của một hình trụ .

Để tính diện tích bề mặt của hình trụ , bạn cần tìm Diện tích cơ sở (B) và Diện tích bề mặt cong (CSA). Do đó, diện tích bề mặt hoặc tổng diện tích của một hình trụ bằng tổng diện tích cơ sở nhân hai lần và diện tích mặt cong.

Mặt cong của hình trụ bằng hình chữ nhật có chiều dài là 2 πr và chiều rộng là h.

trong đó, r = bán kính của mặt tròn và h = chiều cao của hình trụ.

Diện tích mặt cong = Diện tích hình chữ nhật = lxw = πdh

Diện tích cơ sở, B = Diện tích hình tròn = πr ²

Diện tích của một công thức hình trụ

Công thức cho tổng diện tích bề mặt của một hình trụ được cho là:

Tổng diện tích bề mặt của hình trụ = 2πr ² + 2πrh

TSA = 2πr ² + 2πrh

Trong đó, 2πr ² là diện tích của mặt tròn trên và dưới và 2πrh là diện tích của mặt cong.

Bằng cách lấy 2πr làm thừa số chung từ RHS, chúng ta nhận được;

TSA = 2πr (h + r) ……………………………………. ( Diện tích bề mặt của một công thức hình trụ )

Hãy giải các bài toán ví dụ liên quan đến diện tích bề mặt của một hình trụ.

ví dụ 1

Tìm diện tích toàn phần của hình trụ có bán kính 5 cm và chiều cao là 7 cm.

Giải pháp

Theo công thức,

TSA = 2πr (h + r)

= 2 x 3,14 x 5 (7 + 5)

= 31,4 x 12

= 376,8 cm ²

Ví dụ 2

Tìm bán kính của hình trụ có tổng diện tích bề mặt là 2136,56 feet vuông và chiều cao là 3 feet.

Giải pháp

Được:

TSA = 2136,56 bộ vuông

Chiều cao, h = 3 feet

Nhưng, TSA = 2πr (h + r)

2136,56 = 2 x 3,14 xr (3 + r)

2136,56 = 6,28r (3 + r)

Bằng thuộc tính phân phối của phép nhân trên RHS, chúng ta có,

2136,56 = 18,84r + 6,28r ²

Chia mỗi số hạng cho 6,28

340,22 = 3r + r ²

r ² + 3r – 340.22 = 0 ……… ( phương trình bậc hai )

Bằng cách giải phương trình bằng công thức bậc hai, chúng ta nhận được,

r = 17

Do đó, bán kính của hình trụ là 17 feet.

Ví dụ 3

Chi phí sơn một thùng hình trụ là 0,04 đô la cho mỗi cm ² . Tìm chi phí sơn 20 hộp đựng có bán kính 50 cm và chiều cao 80 cm.

Giải pháp

Tính tổng diện tích bề mặt của 20 thùng hàng.

TSA = 2πr (h + r)

= 2 x 3,14 x 50 (80 + 50)

= 314 x 130

= 40820 cm ²

Tổng diện tích bề mặt của 20 container = 40.820 cm ² x 20

= 816.400 cm ²

Chi phí sơn = 816.400 cm ²   x 0,04 đô la mỗi cm ²

= $ 32,656.

Do đó, chi phí sơn 20 container là $ 32,656.

Ví dụ 4

Tìm chiều cao của một hình trụ nếu tổng diện tích bề mặt của nó là 2552 in ² và bán kính là 14 in.

Giải pháp

Được:

TSA = 2552 trong ²

Bán kính, r = 14 in.

Nhưng, TSA = 2πr (h + r)

2552 = 2 x 3,14 x 14 (14 + giờ)

2552 = 87,92 (14 + giờ)

Chia cả hai vế cho 87,92 để được,

29.026 = 14 + giờ

Trừ 14 cho cả hai bên.

h = 15

Do đó, chiều cao của hình trụ là 15 in.

Xem thêm:

Công thức tính diện tích bề mặt của lăng kính

Diện tích bề mặt của một hình cầu – Phương pháp giải hoàn hảo nhất

Diện tích bề mặt bên của xi lanh

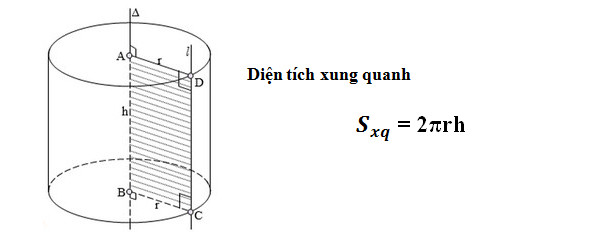
Như đã nói ở trên, diện tích mặt cong của hình trụ được gọi là diện tích bề mặt bên. Nói một cách dễ hiểu, diện tích mặt bên của hình trụ là diện tích bề mặt của hình trụ không bao gồm diện tích mặt đáy và mặt đáy (mặt tròn).

Diện tích mặt bên của hình trụ được cho bởi công thức;

LSA = 2πrh

Ví dụ 5

Tìm diện tích mặt sau của hình trụ có đường kính 56 cm và chiều cao là 20 cm.

Giải pháp

Được:

Đường kính = 56 cm, do đó bán kính, r = 56/2 = 28 cm

Chiều cao, h = 20 cm

Bởi, công thức,

LSA = 2πrh

= 2 x 3,14 x 28 x 20

= 3516,8 cm ² .

Như vậy, diện tích mặt bên của hình trụ là 3516,8 cm ² .

Ví dụ 6

Diện tích bề mặt bên của hình trụ là 144 ft ² . Nếu bán kính của hình trụ là 7 ft, hãy tìm chiều cao của hình trụ.

Giải pháp

Được;

LSA = 144 ft ²

Bán kính, r = 7 ft

144 = 2 x 3,14 x 7 xh

144 = 43,96 giờ

Chia cho cả hai bên là 43,96.

3,28 = h

Vì vậy, chiều cao của hình trụ là 3,28 ft.