Hàm lượng giác chi tiết nhất

Hàm lượng giác

Các hàm lượng giác còn được gọi là một Hàm tròn có thể được định nghĩa đơn giản là các hàm của một góc của một tam giác. Nó có nghĩa là mối quan hệ giữa các góc và các cạnh của một tam giác được cho bởi các hàm số trig. Các hàm lượng giác cơ bản là sin, cosine, tiếp tuyến, cotang, secant và cosecant. Ngoài ra, hãy đọc các nhận dạng lượng giác ở đây.

Có một số công thức và nhận dạng lượng giác biểu thị mối quan hệ giữa các hàm và giúp tìm các góc của tam giác. Tất cả các hàm lượng giác với công thức của chúng đều được giải thích ở đây một cách tỉ mỉ, để độc giả dễ hiểu.

Ngoài ra, bạn sẽ bắt gặp bảng mà giá trị của các tỷ lệ này được đề cập cho một số mức độ cụ thể. Và dựa vào bảng này, bạn sẽ có thể giải được nhiều ví dụ và bài toán lượng giác.

Sáu hàm lượng giác

Các góc của sin, côsin và tiếp tuyến là phân loại cơ bản của các hàm lượng giác. Và ba hàm cotang, secant và cosecant có thể được suy ra từ các hàm chính. Về cơ bản, ba hàm còn lại thường được dùng để so sánh với các hàm lượng giác sơ cấp. Hãy coi sơ đồ sau đây như một tài liệu tham khảo để giải thích về ba chức năng chính này. Sơ đồ này có thể được gọi là tam giác sin-cos-tan. Chúng ta thường xác định lượng giác với sự trợ giúp của  tam giác vuông .

Hàm sin

Hàm sin của một góc là tỷ số giữa độ dài cạnh đối diện với cạnh huyền. Từ sơ đồ trên, giá trị của sin sẽ là:

• Sin a = Đối diện / Hypotenuse = CB / CA

Hàm Cos

Cos của một góc là tỷ số giữa độ dài cạnh kề với độ dài cạnh huyền. Từ sơ đồ trên, hàm cos sẽ được suy ra như sau.

• Cos a = Liền kề / Hypotenuse = AB / CA

Chức năng Tan

Hàm tiếp tuyến là tỷ số giữa độ dài của cạnh đối diện và độ dài của cạnh liền kề. Cần lưu ý rằng tan cũng có thể được biểu diễn dưới dạng sin và cos như tỷ lệ của chúng. Từ sơ đồ ở trên, hàm tan sẽ như sau.

• Tan a = Đối diện / Liền kề = CB / BA

Ngoài ra, về mặt sin và cos, tan có thể được biểu diễn dưới dạng:

Tan a = sin a / cos a

Chức năng Secant, Cosecant và Cotangent

Secant, cosecant (csc) và cotangent là ba hàm bổ sung có nguồn gốc từ các hàm chính của sin, cos và tan. Nghịch đảo của sin, cos và tan lần lượt là cosecant (csc), secant (sec) và cotang (cot). Công thức của mỗi hàm này được đưa ra là:

• Sec a = 1 / (cos a) = Hypotenuse / Liền kề = CA / AB
• Cosec a = 1 / (sin a) = Hypotenuse / Ngược lại = CA / CB
• cot a = 1 / (tan a) = Liền kề / Đối diện = BA / CB

Lưu ý :  Hàm lượng giác nghịch đảo được sử dụng để nhận một góc từ bất kỳ tỉ số lượng giác nào của góc đó . Về cơ bản, nghịch đảo của các hàm sin, cosin, tiếp tuyến, cotang, secant và cosecant được biểu diễn dưới dạng arcsine, arccosine, arctangent, arc cotang, arc secant và arc cosecant.

Công thức

Hãy để chúng tôi thảo luận về các công thức cho trong bảng dưới đây cho các hàm của tỷ số lượng giác (sin, cosin, tiếp tuyến, cotang, secant và cosecant) cho một  tam giác vuông.

Danh tính

Xem thêm:

Công thức lượng giác đầy đủ chi tiết

Hàm lượng giác chi tiết nhất

Dưới đây là các đặc điểm nhận dạng liên quan đến hàm trig.

Chức năng chẵn và lẻ

Các hàm cos và sec là các hàm chẵn; còn lại các hàm khác là hàm lẻ.

sin (-x) = -sin x

cos (-x) = cos x

tan (-x) = – tan x

cot (-x) = -cot x

csc (-x) = -csc x

sec (-x) = sec x

Chức năng định kỳ

Các hàm trig là các hàm tuần hoàn. Chu kỳ tuần hoàn nhỏ nhất là 2π nhưng đối với tiếp tuyến và tọa độ thì nó là π.

sin (x + 2nπ) = sin x

cos (x + 2nπ) = cos x

tan (x + nπ) = tan x

cot (x + nπ) = cot x

csc (x + 2nπ) = csc x

giây (x + 2nπ) = giây x

Trong đó n là số nguyên bất kỳ.

Bản sắc Pythagore

Khi định lý Pythagoras được biểu diễn dưới dạng các hàm lượng giác, nó được cho là đồng dạng của Pythagore. Chủ yếu có ba đặc điểm nhận dạng:

• sin ² x + cos ²  x = 1 [Rất quan trọng]
• 1 + tan ² x = giây ² x
• cosec ² x = 1 + cot ² x

Ba đặc điểm này có tầm quan trọng lớn trong Toán học, vì hầu hết các câu hỏi lượng giác được chuẩn bị trong các kỳ thi dựa trên chúng. Vì vậy, học sinh nên ghi nhớ các đặc điểm nhận dạng này để giải các bài toán đó một cách dễ dàng.

Nhận dạng Tổng và Chênh lệch

• sin (x + y) = sin (x) .cos (y) + cos (x) .sin (y)
• sin (x – y) = sin (x) .cos (y) –cos (x) .sin (y)
• cos (x + y) = cosx.cosy – sinx.siny
• cos (x – y) = cosx.cosy + sinx.siny
• tan (x + y) = [tan (x) + tan (y)] / [1-tan (x) tan (y)]
• tan (xy) = [tan (x) -tan (y)] / [1 + tan (x) tan (y)]

Hàm lượng giác

Bảng

Bảng tỷ lệ lượng giác cho sáu hàm như Sin, Cos, Tan, Cosec, Sec, Cot, là:

Đồ thị

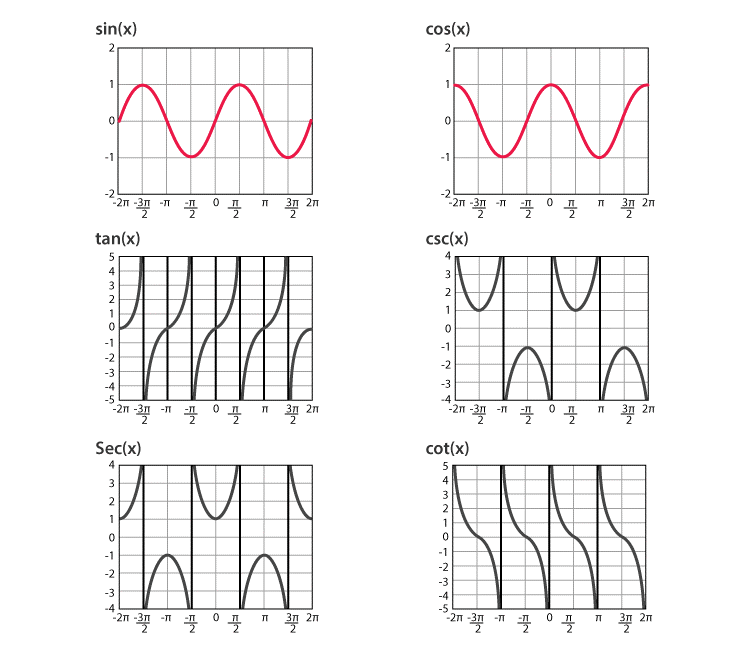
Bây giờ chúng ta đã biết các công thức và giá trị của các góc khác nhau cho tất cả các hàm lượng giác. Chúng ta hãy xem ở đây đồ thị của tất cả sáu hàm lượng giác để hiểu sự thay đổi trong một khoảng thời gian.

Trước khi xem biểu đồ, chúng ta hãy xem miền và phạm vi của mỗi hàm, sẽ được vẽ đồ thị trong mặt phẳng XY.

Đây là biểu đồ cho tất cả các hàm dựa trên miền và phạm vi tương ứng của chúng.

Giải các hàm lượng giác

Các ví dụ đã giải quyết

Ví dụ 1: Tìm các giá trị của Sin 45 °, Cos 60 ° và Tan 60 °.

Bài giải : Sử dụng bảng lượng giác, ta có

Hình sin 45 ° = 1 / √2

Cos 60 ° = 1/2

Tan 60 ° = √3

Ví dụ 2: Đánh giá độ Sin 105 °.

Lời giải : Sin 105 ° có thể được viết là sin (60 ° + 45 °) tương tự như sin (A + B).

Chúng ta biết rằng, công thức sin (A + B) = sin A × cos B + cos A × sin B

Do đó, sin 105 ° = sin (60 ° + 45 °) = sin 60 ° × cos 45 ° + cos 60 ° × sin 45 °

= √3 / 2 × 1 / √2 + 1/2 × 1 / √2

= √3 / 2√2 + 1 / 2√2
= (√3 + 1) / 2√2

Ví dụ 3 : Một cậu bé nhìn thấy một con chim đậu trên cây ở góc độ cao 20 °. If a boy is standing 10 miles away from the tree, at what height bird is sitting?

Bài giải : Xét ABC là tam giác vuông, A là vị trí của con chim, B = cái cây đang chạm đất và C = vị trí của cậu bé.

So BC 10 miles, angle C = 20° and let AB = x miles

Chúng ta biết, tan C = cạnh đối diện / cạnh kề

tan (20 °) = x / 10

hoặc x = 10 × tan (20 °)

hoặc x = 10 × 0,36 = 3,6

Bird is sitting at the height of 3.6 miles from the ground.

Các bài viết liên quan đến lượng giác cho lớp 11 và 12

Đăng ký với BYJU’S để nhận thêm nhiều bài viết liên quan đến toán học như vậy một cách đơn giản và chi tiết. Ngoài ra, hãy đăng ký tại BYJU’S để có hơn 1000 giờ học qua video hấp dẫn cho các môn học và lớp học khác nhau.

Câu hỏi thường gặp – Câu hỏi thường gặp

Sáu hàm lượng giác là gì?

Sáu hàm lượng giác là Sine, Cosine, Tangent, Secant, Cosecant và Cotangent.

Công dụng của hàm lượng giác là gì?

Trong hình học, hàm lượng giác được sử dụng để tìm góc hoặc cạnh chưa biết của tam giác vuông.

Ba hàm lượng giác cơ bản là gì?

Ba hàm lượng giác cơ bản là Sine, Cosine và Tangent.

Công thức của hàm lượng giác là gì?

Nếu θ là một góc của tam giác vuông thì các hàm lượng giác được cho bởi:
sin θ = Cạnh đối của góc θ / Hạ huyền
cos θ = Cạnh kề của góc θ / Hạ huyền
tan θ = Cạnh đối của góc θ / Cận kề
cot θ = Cạnh kề của góc θ /
Cạnh đối của góc
θ = Hạ huyền / Cạnh kề của góc θ cosec θ = Hạ huyền / Cạnh đối diện của góc θ

Giá trị của sin θ, cos θ và tan θ, nếu θ = 30 độ là bao nhiêu?

Nếu θ = 30 độ, thì
Sin θ = sin 30 = ½
Cos θ = cos 30 = √3 / 2
Tan θ = tan 30 = 1 / √3

Khoảng của hàm số sin, cos và tan trong đồ thị tuần hoàn là bao nhiêu?

Hàm sin: y = sinx; Miền: x ∈ R & Phạm vi: – 1 ≤ sin x ≤ 1
Cos Hàm: y = cos x; Miền: x ∈ R & Phạm vi: – 1 ≤ cos x ≤ 1
Tan Hàm: y = tan x; Miền: x ∈ R, x ≠ (2k + 1) π / 2 & Dãy: – ∞ <tan x <∞

Xem thêm: