Tỷ lệ lượng giác chuẩn và chi tiết nhất

Tỷ lệ lượng giác

Sáu tỷ số lượng giác là sin (sin), cosin (cos), tiếp tuyến (tan), cotang (cot), cosecant (cosec) và secant (giây). Trong hình học, lượng giác là một nhánh của toán học liên quan đến các cạnh và góc của một tam giác vuông. Do đó, tỷ lệ trig được đánh giá theo các cạnh và góc.

Các tỉ số lượng giác của một góc cụ thể ‘θ’ được cho dưới đây:

Lưu ý: Cạnh đối diện là cạnh vuông góc và cạnh kề là đáy của tam giác vuông. Ngoài ra, hãy xem các hàm lượng giác để tìm hiểu chi tiết về từng tỷ lệ hoặc hàm số này. Nhận dạng lượng giác

Định nghĩa

Tỷ lệ lượng giác được định nghĩa là giá trị của tất cả các hàm lượng giác dựa trên giá trị của tỷ số các cạnh trong một tam giác vuông.  Tỉ số các cạnh của một tam giác vuông đối với bất kỳ góc nhọn nào của nó được gọi là tỉ số lượng giác của góc cụ thể đó .

Ba cạnh của tam giác vuông là:

• Hypotenuse (cạnh dài nhất)
• Vuông góc (cạnh đối diện với góc)
• Cơ sở (Mặt tiếp giáp với góc)

Những bài viết liên quan:

• Nhận dạng lượng giác
• Tỷ lệ lượng giác của các góc bổ sung
• Tỷ lệ lượng giác của các góc chuẩn
• Góc lượng giác
• Công thức lượng giác
• Giá trị lượng giác

Làm thế nào để Tìm các tỷ số lượng giác?

Xét một tam giác vuông cân tại B.

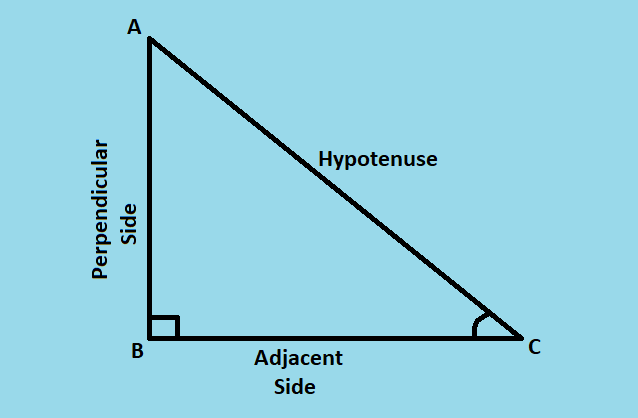
Đối với ∠C, các tỉ số lượng giác được cho là:

• sin: Sine của một góc được định nghĩa là tỷ số của cạnh đối diện (cạnh vuông góc) của góc đó với cạnh huyền.
• cosine: Cosin của một góc được định nghĩa là tỷ số của cạnh kề góc đó với cạnh huyền.
• Tiếp tuyến: Tiếp tuyến của một góc được định nghĩa là tỉ số của cạnh đối diện với góc đó và cạnh kề với góc đó.
• cosecant : Cosecant là một nghịch đảo nhân của sin.
• secant: Secant là một nghịch đảo nhân của cosin.
• cotang: Cotang là nghịch đảo nhân của tiếp tuyến.

Các tỷ số trên được viết tắt lần lượt là sin, cos, tan, cosec, sec và tan theo thứ tự chúng được mô tả. Vì vậy, đối với Δ ABC , các tỷ số được xác định là:

sin C = ( Cạnh đối diện với ∠C) / (Hypotenuse)  = AB / AC

cos C  = ( Cạnh kề ∠C) / (Cạnh huyền)  = BC / AC

tan C  = ( Cạnh đối với ∠C) / (Cạnh đối với ∠C)  = AB / AC  = sin ∠C / cos ∠C

cosec C = 1 / sin C = ( Hypotenuse) / (Cạnh đối diện với ∠C)  =  AC / AB

sec C  = 1 / cos C = ( Hypotenuse) / (Cạnh đối diện với ∠C)  = AC / BC

cot C  = 1 / tan C  = ( Cạnh bên ∠C) / (Cạnh bên C) = BC / AB

Trong Δ vuông ABC,  nếu giả sử ∠ A  và ∠ C  là 30 °  và 60 ° , thì có thể có vô số tam giác vuông với các đặc điểm đó nhưng tất cả các tỷ số được viết ở trên cho ∠ C  trong tất cả các tam giác đó sẽ giống nhau. Vì vậy, tất cả các tỷ số của bất kỳ góc nhọn nào (hoặc ∠ A  hoặc ∠ C ) sẽ giống nhau đối với mọi tam giác vuông. Điều này có nghĩa là các tỷ lệ không phụ thuộc vào độ dài các cạnh của tam giác.

Bảng tỷ lệ lượng giác

Xem thêm:

Công thức lượng giác đầy đủ chi tiết

Hàm lượng giác chi tiết nhất

Các tỷ số lượng giác cho một số góc cụ thể như 0 °, 30 °, 45 °, 60 ° và 90 ° được đưa ra dưới đây, thường được sử dụng trong các phép tính toán học.

Từ bảng này, chúng ta có thể tìm giá trị của các tỉ số lượng giác đối với các góc này. Ví dụ như:

• Sin 30 ° = ½
• Cos 90 ° = 0
• Tan 45 ° = 1

Ứng dụng lượng giác

Lượng giác là một trong những ngành quan trọng nhất của toán học. Một số ứng dụng của lượng giác là:

• Đo chiều cao của tháp hoặc núi lớn
• Xác định khoảng cách của bờ biển
• Tìm khoảng cách giữa hai thiên thể
• Xác định sản lượng điện của các tấm pin mặt trời ở các độ nghiêng khác nhau
• Biểu diễn các đại lượng vật lý khác nhau như sóng cơ, sóng điện từ, v.v.

Rõ ràng là từ các ví dụ trên, lượng giác có liên quan đến một phần quan trọng trong cuộc sống hàng ngày của chúng ta và nhiều hơn nữa. Trong hầu hết các ứng dụng được liệt kê ở trên, một cái gì đó đang được đo lường và đó là tất cả những gì về lượng giác.

Các vấn đề đã được giải quyết

H.1: Nếu trong tam giác vuông ABC, vuông cân tại B, cạnh huyền AC = 5cm, cạnh đáy BC = 3cm và vuông góc AB = 4cm và nếu ∠ACB = θ thì ta tìm tan θ, sin θ và cos θ .

Sol: Đã cho,

Trong ∆ABC,

Hypotenuse, AC = 5cm

Cơ sở, BC = 3 cm

Vuông góc, AB = 4cm

Sau đó,

tan θ = Vuông góc / Cơ sở = 4/3

Hình sin θ = Vuông góc / Hạ huyền = AB / AC = ⅘

Cos θ = Cơ sở / Hypotenuse = BC / AC = ⅗

Q.2: Tìm giá trị của tan θ nếu sin θ = 12/5 và cos θ = ⅗.

Sol: Cho trước, sin θ = 12/5 và cos θ = ⅗

Như chúng ta biết,

Tan θ = Sin θ / Cos θ

Tấn θ = (12/5) / (⅗)

Tấn θ = 12/3

Tấn θ = 4

Câu hỏi thực hành

1. Tìm giá trị của sin θ, nếu tan θ = ¾ và cos θ = ½.
2. Tìm tan θ nếu sin θ = 4/3 và cos θ = 3/2
3. Tìm giây θ, nếu cos θ = 9/8
4. Tìm cosec θ, nếu sin θ 16/5

Tỷ lệ lượng giác của các góc hợp chất

Tải xuống Ứng dụng BYJU’S và tìm hiểu hàng nghìn khái niệm tại đây thông qua các video thú vị và được cá nhân hóa.

Câu hỏi thường gặp – Câu hỏi thường gặp

Ba tỉ số lượng giác chính là gì?

Ba tỉ số lượng giác chính là tiếp tuyến (tan), sin (sin) và côsin (cos).

Sáu tỉ số lượng giác là gì?

Sáu 6 tỉ số lượng giác là sin, cosin, tiếp tuyến, cotang, cosecant và secant.

SOH CAH TOA là gì?

SOH CAH TOA là điều cần nhớ để ghi nhớ công thức các tỉ số lượng giác, sao cho:
SOH: Hàm số
sin là tỉ số Cạnh đối và Cạnh huyền CAH: Cosin là tỉ số Cạnh kề và Cạnh huyền
TOA: Tiếp tuyến là tỉ số Cạnh đối và Mặt liền kề

Công thức của Cotangent, Secant và Cosecant là gì?

Cotangent là tỷ số của cạnh kề và cạnh đối diện, (Cơ sở / vuông góc)
Secant là tỷ lệ cạnh huyền và cạnh kề, (
Hypotenuse / Base) Cosecant là tỷ lệ cạnh huyền và cạnh đối diện (Hypotenuse / Vuông góc)

Mối quan hệ giữa sin, cos và tan là gì?

Hàm số tiếp tuyến bằng tỉ số của hàm số sin và hàm số côsin.
Tan θ = Sin θ / Cos θ

Xem thêm: