Hình elip có dạng hình bầu dục và diện tích của elip được xác định bởi trục chính và trục nhỏ của nó. Diện tích hình elip = πab , trong đó a và b là độ dài của trục bán chính và trục nhỏ của hình elip. Hình elip tương tự như các phần khác của phần hình nón như parabol và hyperbola, có hình dạng mở và không bị ràng buộc.
Mục lục:
|
Định nghĩa
Một hình elip nếu chúng ta nói về quỹ tích, nó là tập hợp tất cả các điểm trên mặt phẳng XY, mà khoảng cách từ hai điểm cố định (được gọi là foci) cộng lại thành một giá trị không đổi.
Hình elip là một trong những phần hình nón, được tạo ra, khi một mặt phẳng cắt hình nón một góc với mặt đáy. Nếu hình nón cắt bởi mặt phẳng, song song với mặt đáy thì nó tạo thành một đường tròn.
Hình elip
Trong hình học, hình elip là một hình dạng hai chiều, được xác định dọc theo các trục của nó. Một hình elip được tạo thành khi một hình nón được cắt bởi một mặt phẳng một góc so với mặt đáy của nó.
Nó có hai tiêu điểm. Tổng của hai khoảng cách đến tiêu điểm, đối với tất cả các điểm trên đường cong, luôn không đổi.
Hình tròn cũng là một hình elip, trong đó các tiêu điểm ở cùng một điểm, là tâm của hình tròn.
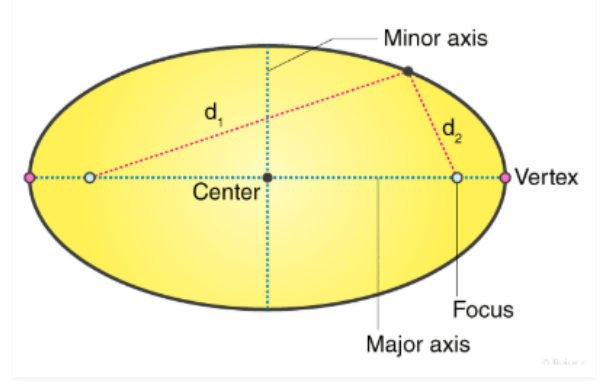
Trục chính và trục nhỏ
Hình elip được xác định bởi hai trục dọc theo trục x và trục y:
- Trục chính
- Trục nhỏ
Trục chính là đường kính dài nhất của hình elip (thường được ký hiệu là ‘a’), đi qua tâm từ đầu này đến đầu kia, ở phần rộng của hình elip . Trong khi trục nhỏ là đường kính ngắn nhất của hình elip (ký hiệu là ‘b’), đi qua tâm ở phần hẹp nhất.
Một nửa trục chính được gọi là bán trục chính và nửa trục nhỏ được gọi là bán trục nhỏ.
Tính chất
- Hình elip có hai tiêu điểm, còn được gọi là tiêu điểm.
- Khoảng cách cố định được gọi là ma trận trực tiếp.
- Độ lệch tâm của hình elip nằm trong khoảng từ 0 đến 1. 0≤e <1
- Tổng mỗi khoảng cách từ quỹ tích của hình elip đến hai tiêu điểm là không đổi
- Hình elip có một trục chính và một trục nhỏ và tâm
Độ lệch tâm của hình elip
Tỷ lệ khoảng cách từ tâm của hình elip từ một trong hai tiêu điểm đến bán trục chính của elip được định nghĩa là độ lệch tâm của elip.
Độ lệch tâm của elip, e = c / a
Trong đó c là tiêu cự và a là độ dài của bán trục chính.
Vì c ≤ a nên độ lệch tâm luôn lớn hơn 1 trong trường hợp hình elip.
Ngoài ra,
c 2 = a 2 – b 2
Do đó, độ lệch tâm trở thành:
e = √ (a 2 – b 2 ) / a
e = √ [(a 2 – b 2 ) / a 2 ] e = √ [1- (b 2 / a 2 )]
Phương trình hình elip
Khi tâm của hình elip ở gốc tọa độ (0,0) và các điểm nằm trên trục x và trục y, thì chúng ta có thể dễ dàng suy ra phương trình elip.
Phương trình của elip được cho bởi;
x 2 / a 2 + y 2 / b 2 = 1
Suy ra phương trình hình elip
Bây giờ, chúng ta hãy xem nó được bắt nguồn như thế nào.
.
Hình trên biểu diễn một hình elip sao cho P 1 F 1 + P 1 F 2 = P 2 F 1 + P 2 F 2 = P 3 F 1 + P 3 F 2 là một hằng số. Hằng số này luôn lớn hơn khoảng cách giữa hai tiêu điểm. Khi cả hai tiêu điểm được nối với sự trợ giúp của một đoạn thẳng thì điểm giữa của đoạn thẳng này nối với tiêu điểm được gọi là tâm, O đại diện cho tâm của hình elip trong hình bên dưới:
Đoạn thẳng đi qua trọng tâm của elip là trục chính và đoạn thẳng vuông góc với trục chính và đi qua tâm của elip là trục nhỏ. Các điểm cuối A và B như hình vẽ được gọi là các đỉnh biểu diễn giao điểm của các trục chính với hình elip. ‘2a’ biểu thị độ dài của trục chính và ‘a’ là độ dài của bán trục chính. ‘2b’ là độ dài của trục nhỏ và ‘b’ là độ dài của nửa trục nhỏ. ‘2c’ đại diện cho khoảng cách giữa hai tiêu điểm.
Bằng chứng:
Chúng ta hãy xem xét các điểm cuối A và B trên trục chính và điểm C và D ở cuối trục nhỏ.
Tổng khoảng cách của B từ F 1 là F 1 B + F 2 B = F 1 O + OB + F 2 B (Từ hình trên)
⇒ c + a + a – c = 2a
Tổng khoảng cách từ điểm C đến F 1 là F 1 C + F 2 C
⇒ F 1 C + F 2 C = √ (b 2 + c 2 ) + √ (b 2 + c 2 ) = 2√ (b 2 + c 2 )
Theo định nghĩa của ellipse;
2√ (b 2 + c 2 ) = 2a
⇒
a = √ (b 2 + c 2 )
⇒ a 2 = b 2 + c 2
⇒
c 2 = a 2 – b 2
Các trường hợp đặc biệt:
- Nếu c = 0 thì F 1 và F 2 , tức là cả hai foci hợp nhất với nhau thành tâm của ellipse. Ngoài ra a 2 trở thành bằng b 2 , tức là a = b nên bây giờ chúng ta nhận được một đường tròn trong trường hợp này.
- Nếu c = a thì b trở thành 0 và ta được đoạn thẳng F 1 F 2 .
Phương trình chuẩn của Elip
Phương pháp đơn giản nhất để xác định phương trình của một hình elip là giả sử rằng tâm của elip là tại điểm gốc (0, 0) và các tiêu điểm nằm trên trục x hoặc trục y của mặt phẳng Descartes như hình dưới đây:
Cả hai tiêu điểm đều nằm trên trục x và tâm O nằm tại gốc tọa độ.
Chúng ta hãy xem hình (a) để suy ra phương trình của một elip. Gọi tọa độ của F 1 và F 2 lần lượt là (-c, 0) và (c, 0) như hình bên. Ta xét điểm P (x, y) nằm trên elip sao cho P thỏa mãn định nghĩa, tức là tổng khoảng cách của P từ F 1 và F 2 trong mặt phẳng là một hằng số 2a.
⇒ PF 1 + PF 2 = 2a – – – (1)
Sử dụng công thức khoảng cách, khoảng cách có thể được viết là:
Bình phương và đơn giản hóa cả hai bên, chúng tôi nhận được;
Bây giờ vì P nằm trên elip nên thỏa mãn phương trình 2 sao cho 0 <c <a.
Vì vậy,
Khi đơn giản hóa,
PF 1 = a + (c / a) x
Tương tự,
PF 2 = a – (c / a) x
Vì thế,
PF 1 + PF 2 = 2a
Do đó phương trình của hình elip có tâm tại gốc và trục chính dọc theo trục x là:
trong đó –a ≤ x ≤ a.
Tương tự, phương trình của hình elip với tâm tại gốc và trục chính dọc theo trục y là:
PDF cho công thức
Nhấp vào đây để tải xuống các phương trình và công thức của một hình elip – Tải xuống PDF
Công thức hình elip
Như chúng ta đã biết, hình elip là một cấu trúc hình khép kín trong một mặt phẳng hai chiều. Do đó, nó bao gồm một vùng trong mặt phẳng 2D. Vì vậy, vùng giới hạn này của hình elip là diện tích của nó. Hình dạng của hình elip khác với hình tròn , do đó công thức tính diện tích của nó cũng sẽ khác.
Diện tích hình elip
Diện tích của hình tròn được tính dựa trên bán kính của nó, nhưng diện tích của hình elip phụ thuộc vào độ dài của trục nhỏ và trục chính. Kiểm tra thêm tại đây: Diện tích hình elip .
Diện tích hình tròn = πr 2
Và,
Diện tích hình elip = π x Trục bán chính x Trục bán nhỏ
| Diện tích hình elip = π.ab |
Chu vi hình elip
Chu vi của một hình elip là tổng khoảng cách chạy bởi đường biên bên ngoài của nó. Đối với một đường tròn, ta dễ dàng tìm được chu vi của nó, vì khoảng cách từ tâm đến bất kỳ điểm nào trên quỹ tích của đường tròn là như nhau. Khoảng cách này được gọi là bán kính.
Nhưng trong trường hợp của một hình elip, chúng ta có hai trục, chính và phụ, đi qua tâm và cắt nhau. Do đó, chúng tôi sử dụng một công thức gần đúng để tìm chu vi của một hình elip, được cho bởi:
p ≈ 2 πa2+b22—-√
Trong đó a và b là độ dài của trục bán chính và trục bán phụ tương ứng.
Bên phải
Các đoạn thẳng vuông góc với trục chính qua bất kỳ điểm nào sao cho điểm cuối của chúng nằm trên hình elip được xác định là trực tràng latus.
Các chiều dài của trực tràng latus là 2b 2 / a.
L = 2b 2 / a
trong đó a và b là độ dài của trục nhỏ và trục chính.
Ngoài ra, hãy đọc:
|
Vấn đề và Giải pháp
Q.1: Nếu độ dài của nửa trục chính là 7cm và nửa trục chính là 5cm của một hình elip. Tìm khu vực của nó.
Giải: Cho trước, độ dài bán trục chính của hình elip, a = 7cm
chiều dài của nửa trục nhỏ của hình elip, b = 5cm
Bằng công thức về diện tích của một hình elip, chúng ta biết;
Diện tích = π xaxb
Diện tích = π x 7 x 5
Diện tích = 35 π
hoặc là
Diện tích = 35 x 22/7
Diện tích = 110 cm 2
Để tìm hiểu thêm về các phần conic, vui lòng tải xuống BYJU’S- Ứng dụng Học tập.
Câu hỏi thường gặp – Câu hỏi thường gặp
Hình elip là gì?
Trục chính và trục nhỏ của elip là gì?
Trục nhỏ nằm dọc theo trục y và là chiều rộng nhỏ nhất trên nó. Nó có chiều dài bằng 2b. Các điểm cuối là các đỉnh của trục nhỏ có tọa độ (h, k ± b).
Directrix và độ lệch tâm của elip là gì?
Diện tích của hình elip là gì?
Diện tích = πab
Trong đó a và b lần lượt là bán trục chính và bán trục phụ.
Phương trình của elip là gì?
(x 2 / a 2 ) + (y 2 / b 2 ) = 1
