Contents
Khác biệt hóa là gì?
Sự khác biệt hóa là bản chất của Giải tích. Đạo hàm được định nghĩa là tốc độ thay đổi tức thời của hàm dựa trên một trong các biến của nó. Nó tương tự như việc tìm hệ số góc của tiếp tuyến với hàm số tại một điểm.
Giả sử bạn cần tìm hệ số góc của đường tiếp tuyến với đồ thị tại điểm P. Hệ số góc có thể được tính gần đúng bằng cách vẽ một đường thẳng qua điểm P và tìm hệ số góc bằng một đường được gọi là đường thẳng.
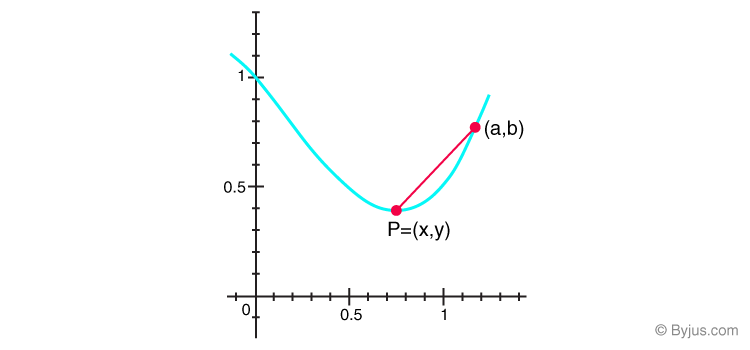

Một hàm số f theo x được cho là khả vi tại điểm x = a, nếu đạo hàm f ‘(a) tồn tại tại mọi điểm trong miền của nó. Đạo hàm của hàm f (x) được cho bởi:


Đối với một hàm khả vi tại bất kỳ điểm nào x = a, trong miền của nó, nó phải liên tục tại điểm cụ thể đó nhưng ngược lại không nhất thiết phải luôn luôn đúng. Miền của f ‘(x) được xác định bởi sự tồn tại của các giới hạn của nó.
Nếu y = f (x) là một hàm theo x, thì đạo hàm của f (x) được cho dưới dạng dy / dx. Điều này được gọi là đạo hàm của y đối với x.
Ngoài ra, đạo hàm của hàm f (x) tại x = a, được cho bởi:


Đạo hàm của hàm f (x) biểu thị tốc độ thay đổi của hàm f (x) đối với x tại điểm ‘a’, nằm trong miền của nó.
Tìm hiểu chi tiết: Sự khác biệt
Nếu đạo hàm của hàm, f ‘, được biết là phân biệt trong miền của nó thì chúng ta có thể tìm thấy hàm f. Trong phép tính tích phân, ta gọi f là phản đạo hàm hay nguyên hàm của hàm f ‘. Phương pháp tính phản đạo hàm được gọi là phản phân biệt hoặc tích phân.
Tích hợp là gì?
Tích phân là một phương pháp để tìm các tích phân xác định và không xác định. Tích phân của một hàm f (x) được cho bởi F (x) và nó được biểu diễn bởi:
![]()
![]()
Ở đâu
RHS của phương trình chỉ ra tích phân của f (x) đối với x
F (x) được gọi là phản đạo hàm hay nguyên hàm.
f (x) được gọi là tích phân.
dx được gọi là tác nhân tích phân.
C là hằng số tích phân hoặc hằng số tùy ý.
x là biến của tích phân.
Tích phân này được gọi là tích phân không xác định, bởi vì các giới hạn không được xác định ở đây.
Bây giờ đối với một hàm f (x) và bất kỳ khoảng đóng nào nói rằng [a, b], tích phân xác định được cho bởi:
∫ a b f (x) dx
Từ những thảo luận trên, có thể nói, phân hóa và tích hợp là quá trình ngược chiều của nhau.
Tìm hiểu thêm: Tích hợp
Công thức phân biệt và tích hợp
Ở đây chúng ta cùng thảo luận về các công thức chung được sử dụng trong tích hợp và phân hóa.
| Công thức phân biệt | Công thức tích hợp |
| d / dx (a) = 0 trong đó a là hằng số | ∫ 1 dx = x + C |
| d / dx (x) = 1 | ∫ a dx = ax + C |
| d / dx (x n ) = nx n-1 | ∫ x n dx = (x n + 1 / n + 1) + C |
| d / dx sin x = cos x | ∫ sin x dx = -cos x + C |
| d / dx cos x = -sin x | ∫ cos x dx = sin x + C |
| d / dx tan x = giây 2 x | ∫ giây 2 x dx = tan x + C |
| d / dx ln x = 1 / x | ∫ (1 / x) dx = ln x + C |
| d / dx e x = e x | ∫ e x dx = e x + C |
Cũng kiểm tra:
- Công thức phân biệt
- Quy tắc tích hợp
Thuộc tính của khác biệt hóa và tích hợp
Bây giờ chúng ta hãy so sánh sự khác biệt và tích hợp dựa trên các thuộc tính của chúng:
- Phân biệt và tích phân đều thỏa mãn tính chất tuyến tính, tức là k 1 và k 2 là các hằng số trong các phương trình trên.
ddx[k1f1( x ) +k2f2( x ) ] =k1ddxf1( x ) +k2ddxf2( x )
∫[k1f1( x ) +k2f2( x ) ] dx =k1∫f1( x ) dx +k2∫f2( x ) dx
- Khác biệt hóa và Tích hợp, cả hai hoạt động đều liên quan đến các giới hạn cho quyết định của chúng.
- Cả sự khác biệt và tích hợp, như đã thảo luận đều là các quá trình nghịch đảo của nhau.
- Đạo hàm của bất kỳ hàm nào là duy nhất nhưng mặt khác, tích phân của mọi hàm không phải là duy nhất. Hai tích phân của cùng một hàm có thể khác nhau một hằng số.
- Khi phân biệt một hàm đa thức, bậc của kết quả nhỏ hơn bậc của hàm đa thức 1 trong khi trong trường hợp tích phân, kết quả thu được có bậc lớn hơn bậc của hàm đa thức 1 bậc.
- Trong khi xử lý các đạo hàm, chúng ta có thể xem xét đạo hàm tại một điểm trong khi, trong tích phân, tích phân của một hàm trên một khoảng được coi là.
- Về mặt hình học, đạo hàm của một hàm mô tả tốc độ thay đổi của một đại lượng đối với một đại lượng khác trong khi tích phân không xác định biểu thị họ các đường cong nằm song song với nhau có các tiếp tuyến song song tại giao điểm của mọi đường cong họ với các đường trực giao. đến trục đại diện cho biến tích hợp.
Xem thêm: