Contents
Khoảng cách giữa điểm và dòng xuất phát
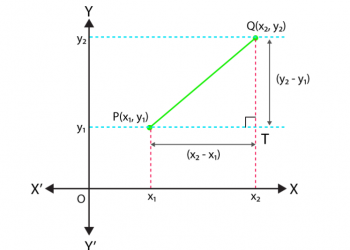
Các phương trình tổng quát của một dòng được đưa ra bởi Axe + By + C = 0. Hãy xem xét một P điểm trong mặt phẳng tọa độ Descartes có (x 1 , y 1 ). Khoảng cách từ điểm đến đoạn thẳng, trong hệ Descartes, được cho bằng cách tính độ dài của đường vuông góc giữa điểm và đoạn thẳng.
Trong hình bên dưới, khoảng cách giữa điểm P và đường thẳng LL có thể được tính bằng cách tính độ dài của đường vuông góc.
Vẽ PQ từ P đến đường thẳng L.


Các điểm tọa độ cho các điểm khác nhau như sau:
Điểm P (x 1 , y 1 ), Điểm N (x 2 , y 2 ), Điểm R (x 3 , y 3 )
Đường thẳng L giao nhau trên cả trục x và trục y lần lượt tại các điểm N và M. Tọa độ của những điểm này là và .M( 0 , –CB)N ( –CA, 0 )
Diện tích Δ MPN có thể được cho là:
Diện tích Δ MPN =12 × B a s e × H e tôi gh t
⇒ A r e a o f Δ M PN =12 × P Q × M N
⇒ PQ = ……………………… (i)2 × A r e a o f Δ M PNMN
Về mặt hình học tọa độ, diện tích của tam giác được cho là:
Diện tích Δ MPN =12[x1(y2–y3) +x2(y3–y1) +x3(y1–y2) ]
Do đó, diện tích của tam giác có thể được cho là:
Diện tích Δ MPN=12[x1( 0 +CB) + ( –CA) ( –CB–y1) + 0 (y1– 0 ) ]
⇒ A r e a o f Δ M PN =12[CB×x1+CA×y1+ (c2A B) ) ]
Giải biểu thức này ta nhận được;
2 × A r e a o f Δ M PN = (CA B) (Ax1+ By1+ C) ………………………… (ii)
Sử dụng công thức khoảng cách, chúng ta có thể tìm ra độ dài cạnh MN của ∆MPN.
MN=( 0 +CA)2+(CB– 0 )2——————√
⇒ MN=CA BA2+B2——-√ ………………………………… .. (iii)
Lập phương trình (ii) và (iii) trong (i), giá trị của vuông góc là:
PQ =| Ax1+ By1+ C|A2+B2√
Chiều dài này thường được biểu thị bằng .d
Khoảng cách giữa hai đường thẳng song song
Khoảng cách giữa hai đường thẳng song song bằng khoảng cách vuông góc giữa hai đường thẳng đó. Ta biết rằng hệ số góc của hai đường thẳng song song là như nhau; do đó phương trình của hai đường thẳng song song có thể được cho là:
y = và =m x + c1ym x + c2
Điểm là giao điểm của đường thẳng thứ hai trên trục .Ax


Khoảng cách vuông góc sẽ là khoảng cách cần thiết giữa hai đường
Khoảng cách giữa điểm và đường thẳng = có thể được đưa ra bằng cách sử dụng công thức:Aym x + c2
d =| Ax1+ By1+ C|A2+B2√
⇒ d =∣∣( – m ) (–c1m) –c2∣∣1 +m2√
⇒ d =|c1–c2|1 +m2√
Do đó, chúng ta có thể kết luận rằng khoảng cách giữa hai đường thẳng song song là:
d =|c1 – c2|√ 1+m2
Nếu chúng ta coi dạng tổng quát của phương trình đường thẳng và các đường thẳng được cho bởi:
L1 : A x + B y + C1 =0
L2 : A x + B y + C2 =0
Sau đó, khoảng cách giữa chúng được cho bởi:
d =|C1 – C2|√A2 + B2
Khoảng cách ngắn nhất giữa hai đường thẳng song song
Khoảng cách ngắn nhất giữa hai đường thẳng song song có thể được xác định bằng cách sử dụng độ dài của đoạn vuông góc giữa các đường thẳng. Không quan trọng bạn đang chọn đường vuông góc nào, miễn là hai điểm nằm trên đường thẳng.
Như vậy, bây giờ chúng ta có thể dễ dàng tính được khoảng cách giữa hai đường thẳng song song và khoảng cách giữa một điểm và một đường thẳng.
Xem thêm: