Sự thật:
|
Tổng của cả ba góc của một tam giác đều bằng 180 độ.
60 ° + 60 ° + 60 ° = 180 °
Do đó, nó tuân theo tính chất tổng góc của tam giác .
Bình đẳng được hình thành bởi sự kết hợp của hai từ, tức là, “Equi” có nghĩa là ngang bằng và “Bên” có nghĩa là các bên. Một tam giác đều còn được gọi là một đa giác đều hoặc tam giác đều vì tất cả các cạnh của nó đều bằng nhau.
Ngoài ra, hãy tìm hiểu : Các loại hình tam giác
Mục lục:
|
Định nghĩa
Như chúng ta đã thảo luận trong phần giới thiệu, tam giác đều là tam giác có tất cả các cạnh của nó có độ dài bằng nhau. Ngoài ra, ba góc của tam giác đều đồng dạng và bằng 60 độ.
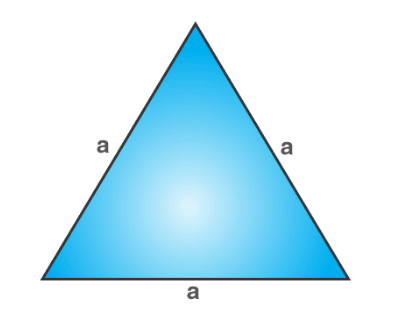

Giả sử ABC là tam giác đều, theo định nghĩa;
AB = BC = AC, trong đó AB, BC và AC là các cạnh của tam giác đều.
Và
∠A = ∠B = ∠C = 60 °
Dựa trên các cạnh có hai loại hình tam giác khác:
Các tính chất cơ bản
- Cả ba cạnh đều bằng nhau.
- Cả ba góc đều đồng dư và bằng 60 độ.
- Nó là một đa giác đều với ba cạnh.
- Đường vuông góc vẽ từ đỉnh của tam giác đều đến cạnh đối diện sẽ chia nó thành hai nửa bằng nhau. Ngoài ra, góc của đỉnh từ nơi vuông góc được vẽ được chia thành hai góc bằng nhau, tức là mỗi góc 30 độ.
- Ortho-center và centroid ở cùng một điểm.
- Trong một tam giác đều, đường trung tuyến, đường phân giác của góc và đường cao đối với tất cả các cạnh đều bằng nhau.
- Diện tích của một tam giác đều là √3a 2 /4
- Chu vi hình tam giác đều là 3a.
So sánh: Bình đẳng, Cân bằng và Scalene
| Tam giác đều | Tam giác cân | Tam giác Scalene |
| Cả ba cạnh đều bằng nhau | Hai cạnh bất kỳ đều bằng nhau | Cả ba mặt đều không bình đẳng |
| Cả ba góc bên trong đều bằng 60 độ | Các góc đối diện với các cạnh bên bằng nhau thì bằng | Tất cả các góc đều không bằng nhau về số đo |
Định lý
Nếu ABC là tam giác đều và P là một điểm trên cung BC của đường tròn ngoại tiếp tam giác ABC thì;
PA = PB + PC
Chứng minh: Cho tứ giác ABPC nội tiếp, ta có;
PA⋅BC = PB⋅AC + PC⋅AB
Vì chúng ta biết, đối với tam giác đều ABC,
AB = BC = AC
Vì thế,
PA.AB = PB.AB + PC.AB
Lấy AB làm chung;
PA.AB = AB (PB + PC)
PA = PB + PC
Do đó, đã chứng minh.
Công thức
Công thức cho diện tích và chu vi được đưa ra ở đây.
Diện tích tam giác đều
Các khu vực của một tam giác đều là khu vực bị chiếm đóng bởi nó trong một mặt phẳng hai chiều. Công thức về diện tích của một tam giác đều được cho bởi:
A = √3a 2 /4
Hãy để chúng tôi suy ra công thức ở đây:


Nếu chúng ta thấy hình trên, diện tích của một tam giác được cho bởi;
Diện tích = ½ x cơ sở x chiều cao
Ở đây Base = a và height = h
Vì thế,
Diện tích = ½ xaxh ……… (1)
Bây giờ, từ hình trên, độ cao h chia đôi cơ sở thành hai nửa bằng nhau, chẳng hạn như a / 2 và a / 2. Nó cũng tạo thành hai tam giác vuông tương đương.
Vì vậy, đối với một tam giác vuông, sử dụng định lý Pythagoras, chúng ta có thể viết:
a 2 = h 2 + (a / 2) 2
hoặc là
h 2 = (a) 2 – (a / 2) 2
= 3a 2 /4
h = √3a / 2
Bằng cách đưa giá trị này vào phương trình 1, chúng ta nhận được;
Diện tích = ½ xax √3a / 2
A = √3a 2 /4
Do đó, diện tích của tam giác đều bằng √3a 2/4 .
Chu vi tam giác đều
Trong hình học, chu vi của một đa giác bất kỳ bằng độ dài các cạnh của nó. Trong trường hợp tam giác đều, chu vi sẽ là tổng của cả ba cạnh.
Giả sử, ABC là tam giác đều, khi đó chu vi ∆ABC là;
Chu vi = AB + BC + AC
P = a + a + a
P = 3a
Trong đó a là độ dài các cạnh của tam giác.
Chiều cao của tam giác đều
Chiều cao hoặc đường cao của một tam giác đều có thể được xác định bằng cách sử dụng định lý Pythagoras. Như chúng ta đã biết, một tam giác đều có tất cả các cạnh bằng nhau. Bây giờ, nếu chúng ta hạ một đường cao từ đỉnh của tam giác xuống đáy, nó sẽ chia tam giác thành hai tam giác vuông bằng nhau.
Như vậy, từ hình trên, chúng ta có thể tìm được chiều cao (h) của tam giác đều, là:
h = √3a / 2
Trong đó a là cạnh của tam giác.
| Khu vực | √3a 2 /4 |
| Chu vi | 3a |
| Độ cao | √3a / 2 |
Tâm của tam giác đều
Trọng tâm của tam giác đều nằm ở tâm của tam giác. Vì tất cả các cạnh của nó đều có độ dài bằng nhau, do đó rất dễ dàng tìm được tâm cho nó.
Để tìm trọng tâm, chúng ta cần vẽ các đường vuông góc từ mỗi đỉnh của tam giác sang các cạnh đối diện. Các đường vuông góc này đều có chiều dài bằng nhau và cắt nhau tại một điểm duy nhất, được gọi là centroid. Xem hình bên dưới:


Lưu ý: Trọng tâm của một tam giác đều ở cách đều tất cả các cạnh và các đỉnh.
Circumcenter
Đường tròn ngoại tiếp tam giác đều là giao điểm của các đường trung trực của các cạnh. Ở đây, đường tròn ngoại tiếp đi qua cả ba đỉnh của tam giác.
Nếu bất kỳ tâm, trực tâm hoặc tâm nào trùng với đường tròn của một tam giác thì nó được gọi là tam giác đều.
Các ví dụ đã giải quyết
Q.1: Tìm diện tích tam giác đều ABC, trong đó AB = AC = BC = 4cm.
Giải pháp:
Theo công thức, chúng tôi biết;
Diện tích = √3a 2 /4
Cho trước a = 4cm
Do đó, bằng cách đặt giá trị mà chúng ta nhận được;
Diện tích = √3 (4) 2 /4
A = 4√3
H.2: Tìm đường cao của một tam giác đều có các cạnh bằng 10cm.
Giải pháp:
Theo công thức chúng tôi biết,
Độ cao của tam giác đều = √3a / 2
Kể từ, a = 10cm
Vì thế,
h = √3 x (10/2)
h = 5√3
Để biết thêm các bài viết liên quan, hãy đăng ký với BYJU’S.
Câu hỏi thường gặp – Câu hỏi thường gặp
Tam giác đều là gì?
Dạng đa giác đều là tam giác đều?
Tên khác nhau của hình tam giác dựa trên các cạnh là gì?
Tam giác
vô hướng
Tam giác cân Tam giác đều
Một tam giác đều có bao nhiêu cạnh?
Chu vi của tam giác đều có cạnh bằng 10cm là bao nhiêu?
Chu vi = 3 x 10 = 30 cms