- Ma trận
- Các loại ma trận
- Ma trận nghịch đảo
- Chuyển vị của ma trận
- Bản ngã
- Tính chất
- Công thức Laplace
- Yếu tố quyết định của một ma trận
- Các ví dụ
- Câu hỏi thường gặp
Định nghĩa ma trận
Ma trận là một dãy số hình chữ nhật có thứ tự, được sử dụng để biểu thị các phương trình tuyến tính. Ma trận có các hàng và cột. chúng ta cũng có thể thực hiện các phép toán trên ma trận như cộng, trừ, nhân ma trận. Giả sử số hàng là m và số cột là n, khi đó ma trận được biểu diễn dưới dạng ma trận m × n.
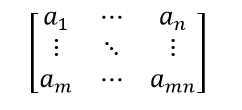
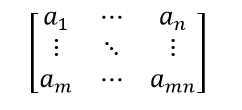
Ngoài ra, hãy đọc:
- Ma trận nghịch đảo 3 x 3
- Ma trận đơn vị
Các loại ma trận
Có nhiều loại ma trận khác nhau. Hãy xem một số ví dụ về các loại ma trận khác nhau
- Ma trận số 0: ⎡⎣⎢000000000⎤⎦⎥
- Ma trận đơn vị: ⎡⎣⎢100010001⎤⎦⎥
- Ma trận đối xứng: ⎡⎣⎢23– 1306– 165⎤⎦⎥
- Ma trận đường chéo: ⎡⎣⎢600090002⎤⎦⎥
- Ma trận tam giác trên: ⎡⎣⎢600– 140522⎤⎦⎥
- Ma trận tam giác dưới: ⎡⎣⎢62số 804– 1002⎤⎦⎥
Nghịch đảo của một ma trận
Nghịch đảo của ma trận thường được định nghĩa cho ma trận vuông. Với mọi ma trận vuông m × n, tồn tại một ma trận nghịch đảo . Nếu A là ma trận vuông thì A -1 là nghịch đảo của ma trận A và thỏa mãn tính chất:
AA -1 = A -1 A = I, trong đó I là ma trận Định danh.
Ngoài ra, định thức của ma trận vuông ở đây không được bằng không.
Chuyển vị của ma trận
Chuyển vị của một ma trận có thể được xác định bởi các hàng cho các cột. Nếu A là một ma trận, thì chuyển vị của một ma trận được đại diện bởi A T .
Ví dụ, chúng ta hãy giả sử một ma trận 3 × 3, Giả sử A, thì chuyển vị của A, tức là A T được cho bởi
A =⎡⎣⎢63725419số 8⎤⎦⎥
AT=⎡⎣⎢62135974số 8⎤⎦⎥
Trong trường hợp, nếu ma trận vuông nhất định là một ma trận đối xứng, thì ma trận A cần được bình đẳng đến A T .
Nó có nghĩa rằng A = A T .
Định nghĩa của Định thức
Một định thức có thể được xác định theo nhiều cách đối với một ma trận vuông.
Cách đầu tiên và đơn giản nhất là xây dựng định thức bằng cách tính đến các phần tử hàng trên cùng và các phần tử phụ tương ứng. Lấy phần tử đầu tiên của hàng trên cùng và nhân nó với phần tử phụ, sau đó trừ tích của phần tử thứ hai và phần tử phụ của nó. Tiếp tục thêm và trừ luân phiên tích của mỗi phần tử của hàng trên cùng với phần tử phụ tương ứng của nó cho đến khi tất cả các phần tử của hàng trên cùng đã được xem xét.
Ví dụ, chúng ta hãy xem xét một ma trận A 4 × 4.


Phương pháp thứ hai để tìm định thức:
Cách thứ hai để xác định một định thức là biểu diễn theo các cột của ma trận bằng cách biểu diễn một ma trận nxn theo các vectơ cột.
Xét các vectơ cột của ma trận A là A = [a 1 , a 2 , a 3 ,… a n ] trong đó phần tử a j bất kỳ là vectơ có kích thước x.
Khi đó định thức của ma trận A được xác định sao cho
Nó [a 1 + a 2 …. ba j + cv… a x ] = b det (A) + c det [a 1 + a 2 +… v… a x ]
Det [a 1 + a 2 …. a j và j + 1 … a x ] = – det [a 1 + a 2 +… a j + 1 a j … a x ]
Nó (I) = 1
Trong đó các đại lượng vô hướng được ký hiệu là b và c, một vectơ có kích thước x được ký hiệu là v và ma trận nhận dạng có kích thước x được ký hiệu là I.
Từ những phương trình này, chúng ta có thể suy ra rằng định thức là một hàm tuyến tính của các cột. Hơn nữa, chúng tôi quan sát thấy rằng dấu hiệu của định thức có thể được hoán đổi cho nhau bằng cách hoán đổi vị trí của các cột liền kề. Ma trận nhận dạng của vô hướng đơn vị tương ứng được ánh xạ bởi hàm đa tuyến tính xen kẽ của các cột. Hàm này là định thức của ma trận.
Kiểm tra: Yếu tố quyết định của ma trận 3 × 3
Thuộc tính của Định thức
- Nếu I n là ma trận nhận dạng của bậc nxn, thì det (I) = 1
- Nếu ma trận M T là chuyển vị của ma trận M thì det (M T ) = det (M)
- Nếu ma trận M -1 là nghịch đảo của ma trận M thì det (M -1 ) =1de t ( M)= it (M) -1
- Nếu hai ma trận vuông M và N có cùng kích thước thì det (MN) = det (M) det (N)
- Nếu ma trận M có kích thước axa và C là hằng số thì det (CM) = C a det (M)
- Nếu X, Y và Z là ba ma trận bán hạn dương có kích thước bằng nhau, thì điều sau đúng cùng với hệ quả det (X + Y) ≥ det (X) + det (Y) cho X, Y, Z ≥ 0 det (X + Y + Z) + det C ≥ det (X + Y) + det (Y + Z)
- Trong ma trận tam giác, định thức bằng tích của các phần tử đường chéo.
- Định thức của ma trận bằng 0 nếu tất cả các phần tử của ma trận bằng 0.
- Công thức Laplace và Ma trận Điều chỉnh
Ngoài các thuộc tính này của định thức, có một số thuộc tính khác, chẳng hạn như
- Thuộc tính phản ánh
- Thuộc tính all-zero
- Thuộc tính Tỷ lệ hoặc Thuộc tính Lặp lại
- Chuyển đổi tài sản
- Tổng tài sản
- Vô hướng nhiều thuộc tính
- Thuộc tính nhân tố
- Thuộc tính Tam giác
- Thuộc tính Bất biến
- Yếu tố quyết định của ma trận Cofactor
Công thức Laplace cho Định thức
Với công thức Laplace, định thức của ma trận có thể được biểu diễn dưới dạng các con của ma trận.
Nếu ma trận B xy là trẻ vị thành niên của ma trận A thu được bằng cách loại bỏ x thứ và y thứ cột và có kích thước
(j-1 x j-1), thì định thức của ma trận A được cho bởi
it (A) = ∑jY= 1( – 1)x + yax , yBx , y
Và ( – 1)x + yBx , y được gọi là đồng yếu tố.
Ma trận bổ trợ thu được bằng cách chuyển vị ma trận chứa các đồng yếu tố và được đưa ra bởi phương trình,
(Điều chỉnh (A)) x, y = (-1) x + y B x, y
Liên kết liên quan đến lớp học:
|
Yếu tố quyết định của một ma trận
Để giải hệ phương trình tuyến tính và tìm nghịch đảo của ma trận, định thức đóng một vai trò quan trọng. Bây giờ, chúng ta hãy thảo luận về cách tìm định thức của ma trận 2 × 2 và ma trận 3 × 3. Nếu A là một ma trận, thì định thức của ma trận A thường được biểu diễn bằng cách sử dụng det (A) hoặc | A |.
Tìm các yếu tố quyết định cho ma trận 2 × 2:
Giả sử chúng ta có một ma trận vuông 2 × 2
A = [a11a21a12a22], sau đó
| A | =∣∣∣a11a21a12a22∣∣∣
| A | =a11a22–a21a12
Tìm các yếu tố quyết định cho ma trận 3 × 3
Bây giờ, giả sử ma trận 3 × 3, nói
A =⎡⎣⎢a11a21a31a12a22a32a13a23a33⎤⎦⎥, sau đó
| A | =∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣
| A | =a11[a22a32a23a33] –a12[a21a31a23a33] +a13[a21a31a22a32]
Ví dụ về yếu tố quyết định và ma trận
Ví dụ 1:
Tìm định thức của ma trận A = [4322]
Giải pháp:
Được: A = [4322]
Định thức của ma trận A là
it (A) = | A | = 8 – 6
| A | = 2
Ví dụ 2 :
Tìm định thức của ma trận A =⎡⎣⎢261354127⎤⎦⎥
Giải pháp:
Được: A =⎡⎣⎢261354127⎤⎦⎥
Vì thế,
| A | =2∣∣∣5427∣∣∣– 3∣∣∣6127∣∣∣+ 1∣∣∣6154∣∣∣
| A | = 2 (35-8) – 3 (42-2) +1 (24-5)
| A | = 2 (27) – 3 (40) + 1 (19)
| A | = 54-120 + 19
| A | = 73 -120
| A | = -47
Các câu hỏi thường gặp về các yếu tố quyết định và ma trận
Xác định ma trận
Ma trận được định nghĩa là một mảng số hình chữ nhật. Tập hợp các số được sắp xếp theo hàng và cột
Định thức có nghĩa là gì?
Định thức được định nghĩa là một giá trị vô hướng được liên kết với ma trận vuông. Nếu X là ma trận thì định thức của ma
Tại sao chúng ta sử dụng các yếu tố quyết định?
Định thức được sử dụng để giải hệ phương trình tuyến tính và nó cũng được sử dụng để tìm nghịch đảo của ma trận.
Đề cập đến các thuộc tính quan trọng của các yếu tố quyết định
Các thuộc tính của định thức là:
Thuộc tính phản ánh Thuộc tính
tam giác
Tất cả không Thuộc
tính tổng Thuộc tính
vô hướng Đa thuộc tính Thuộc tính
nhân tố Thuộc tính
Tỷ lệ
Tính toán phương trình bậc hai dễ hiểu nhất chưa đầy 1 phút
Yếu tố theo nhóm – Làm thế nào để nhân tử của tam thức bằng cách nhóm?