Đạo hàm riêng là gì? Xem xong 5 phút hiểu luôn.

Định nghĩa Đạo hàm một phần

Giả sử, chúng ta có một hàm f (x, y), phụ thuộc vào hai biến x và y, trong đó x và y độc lập với nhau. Khi đó ta nói rằng hàm f phụ thuộc một phần vào x và y. Bây giờ, nếu chúng ta tính đạo hàm của f, thì đạo hàm đó được gọi là đạo hàm riêng của f. Nếu chúng ta phân biệt hàm f với x thì lấy y làm hằng số và nếu chúng ta phân biệt f với y thì lấy x làm hằng số.

Ký hiệu phái sinh một phần

Trong toán học, đạo hàm riêng của bất kỳ hàm nào có một số biến là đạo hàm của nó đối với một trong những biến đó trong đó các biến khác được giữ không đổi. Đạo hàm riêng của hàm f đối với x khác nhau được ký hiệu là f ‘ _x , f _x , ∂ _x f hoặc ∂f / ∂x. Ở đây ∂ là ký hiệu của đạo hàm riêng.

Ví dụ : Giả sử f là một hàm theo x và y thì nó sẽ được biểu diễn bởi f (x, y). Vì vậy, đạo hàm riêng của f đối với x sẽ là ∂f / ∂x giữ cho y là hằng số. Cần lưu ý rằng nó là ∂x, không phải dx. ∂f / ∂x còn được gọi là f _x .

Công thức đạo hàm từng phần

Nếu f (x, y) là một hàm, trong đó f phụ thuộc một phần vào x và y và nếu chúng ta phân biệt f theo x và y thì các đạo hàm được gọi là đạo hàm riêng của f. Công thức tính đạo hàm riêng của f đối với x lấy y làm hằng số được cho bởi;

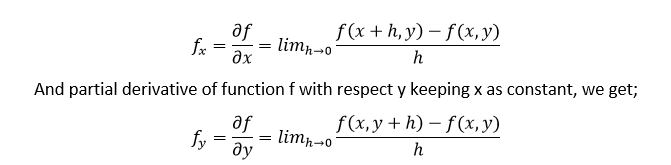
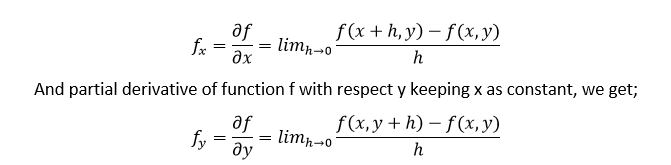
Sự khác biệt từng phần

Quá trình tìm các đạo hàm riêng của một hàm số đã cho được gọi là phân biệt từng phần. Phân biệt từng phần được sử dụng khi chúng ta lấy một trong các đường tiếp tuyến của đồ thị của hàm số đã cho và nhận được hệ số góc của nó. Hãy hiểu điều này với sự trợ giúp của ví dụ dưới đây.

Thí dụ:

Giả sử rằng f là một hàm của nhiều hơn một biến sao cho,

f = x ² + 3xy

Đồ thị của z = x ²  + 3xy được cho dưới đây:

Đồ thị của hàm này biểu diễn một bề mặt trong không gian Euclide. Đối với mỗi điểm trên bề mặt này, có vô số đường tiếp tuyến. Bây giờ, chúng ta có thể áp dụng sự khác biệt từng phần để chọn một trong những đường này và tìm độ dốc của nó.
Để tìm hệ số góc của đường tiếp tuyến với hàm tại một điểm, giả sử P (1,1) và song song với mặt phẳng xz, chúng ta coi y là một hằng số.
Bằng cách tìm đạo hàm của phương trình lấy y làm hằng số, chúng ta có thể nhận được hệ số góc của hàm f đã cho tại điểm (x, y). Điều này có thể được thực hiện như sau.
∂f / ∂x = (∂ / ∂x) (x ² + 3xy) = 2x +
3y Giá trị của ∂f / ∂x tại (1, 1) là:
2 (1) + 3 (1) = 5
Đó có nghĩa là độ dốc là 5.
Do đó, ∂f / ∂x = 5 tại (1, 1).

Quy tắc phái sinh từng phần

Giống như các đạo hàm thông thường, các đạo hàm riêng tuân theo một số quy tắc như quy tắc tích, quy tắc thương số, quy tắc chuỗi, v.v.

Quy tắc nhân

Nếu u = f (x, y) .g (x, y) thì,

Quy tắc thương số

Nếu u = f (x, y) / g (x, y), trong đó g (x, y) ≠ 0, thì;

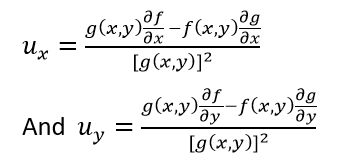
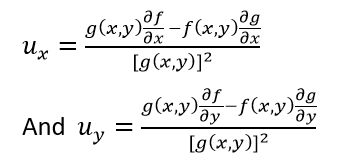
Quy tắc quyền lực

Nếu u = [f (x, y)] ⁿ thì đạo hàm riêng của u đối với x và y được xác định là;

u _x = n | f (x, y) | ^n-1 ∂f / ∂x

Và u _y = n | f (x, y) | ^n-1 ∂f / ∂y

Quy tắc chuỗi

Ở đây, quy tắc chuỗi cho một biến độc lập và hai biến độc lập được đưa ra dưới đây:

Quy tắc chuỗi cho một biến độc lập:

Xét rằng, nếu x = g (t) và y = h (t) là các hàm phân biệt của t và z = f (x, y) là một hàm phân biệt của x và y. Do đó z có thể được viết dưới dạng z = f (g (t), h (t)), là một hàm phân biệt của t, khi đó đạo hàm riêng của hàm đối với biến “t” được cho là:

∂với∂t=∂với∂x.∂x∂t+∂với∂Y.∂Y∂tỞ đây, các đạo hàm thông thường được xác định tại “t”, trong khi các đạo hàm riêng được đánh giá tại (x, y)

Quy tắc chuỗi cho hai biến độc lập:

Giả sử rằng x = g (u, v) và y = h (u, v) là các hàm phân biệt của hai biến u và v, và z = f (x, y) là một hàm phân biệt của x và y, thì z có thể được định nghĩa là z = f (g (u, v), h (u, v)), là một hàm phân biệt của u và v. như:

∂với∂u=∂với∂x∂x∂u+∂với∂Y∂Y∂uvà

∂với∂v=∂với∂x∂x∂v+∂với∂Y∂Y∂v

Đạo hàm một phần của lôgarit tự nhiên (Trong)

Để tìm đạo hàm riêng của lôgarit tự nhiên “In”, chúng ta phải tiến hành quy trình tương tự như tìm đạo hàm của hàm thông thường. Nhưng, ở đây khi chúng ta tính toán đạo hàm riêng của hàm đối với một biến độc lập nhận một biến khác là hằng số và tuân theo điều tương tự với những biến khác.

Ví dụ về phái sinh một phần

Ví dụ 1: Xác định đạo hàm riêng của hàm số: f (x, y) = 3x + 4y.

Giải pháp:

Cho hàm số: f (x, y) = 3x + 4y

Để tìm ∂f / ∂x, hãy giữ y là hằng số và phân biệt hàm:

Do đó, ∂f / ∂x = 3

Tương tự, để tìm ∂f / ∂y, hãy giữ x là hằng số và phân biệt hàm:

Do đó, ∂f / ∂y = 4

Ví dụ 2: Tìm đạo hàm riêng của f (x, y) = x ² y + sin x + cos y.

Giải pháp:

Bây giờ, hãy tìm ra f _x trước tiên giữ cho y là hằng số

f _x = ∂f / ∂x = (2x) y + cos x + 0

= 2xy + cos x

Khi chúng ta giữ y như một hằng số thì cos y trở thành một hằng số để đạo hàm của nó trở thành không.

Tương tự, tìm f _y

f _y = ∂f / ∂y = x ² + 0 + (-sin y)

= x ² – sin y

Ví dụ 3: Tìm ∂f / ∂x, ∂f / ∂y, ∂f / ∂z của hàm số đã cho, f (x, y, z) = x cos z + x ² y ³ e ^z

Giải pháp:

Để tìm ∂f / ∂x, ∂f / ∂y, ∂f / ∂z

Cho Hàm số: f (x, y, z) = x cos z + x ² y ³ e ^z

∂f / ∂x = cos z + 2xy ³ e ^z

∂f / ∂y = 3x ² y ² e ^z

∂f / ∂z = -x sin z + x ² y ³ e ^z

Để tìm hiểu thêm các bài toán về đạo hàm part al và các lỗi liên quan đến phương trình khác nhau , hãy đăng ký BYJU’S – Ứng dụng Học tập và tải xuống ứng dụng để tìm hiểu tất cả các khái niệm quan trọng liên quan đến Toán học một cách dễ dàng.