Dạng chặn của phương trình mặt phẳng
Có vô số mặt phẳng vuông góc với một vectơ cụ thể như chúng ta đã thảo luận trong các phần trước của chúng ta. Nhưng khi nói về một điểm cụ thể chỉ xảy ra một mặt phẳng riêng vuông góc với điểm đi qua khu vực đã cho. Điều này có thể được biểu thị bằng phương trình vectơ cụ thể sau:
( [latex] \ vec {r} – \ vec {a} [/ latex] ). [latex] \ vec {N} [/ latex]
Ở đây, [latex] \ vec {r} [/ latex] và [latex] \ vec {a} [/ latex] biểu thị vectơ vị trí
Ký hiệu của loại mặt phẳng này trong một phương trình Descartes như sau:
[latex] A (x- {x} _ {1}) + B (y- {y} _ {1}) + C (z – {z} _ {1}) = 0 [/ latex]
Tỷ lệ hướng ở đây được ký hiệu là A, B và C.
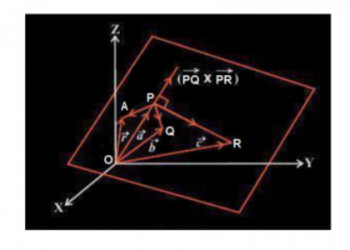
Ngoài ra, phương trình của một mặt phẳng đi qua ba điểm không thẳng hàng ở dạng vectơ được cho là:
[latex] (\ vec {r} – \ vec {a}). [(\ vec {b} – \ vec {a}) × (\ vec {c} – \ vec {a})] = 0 [/ mủ cao su]
Phương trình của một mặt phẳng ở dạng Descartes đi qua ba điểm không thẳng hàng được cho là:


Bây giờ chúng ta hãy thảo luận về phương trình của một mặt phẳng ở dạng chặn.
Phương trình tổng quát của một mặt phẳng được cho là:
Ax + By + Cz + D = 0 (D ≠ 0)
Bây giờ chúng ta hãy thử xác định phương trình của một mặt phẳng theo các giao tuyến được tạo thành bởi mặt phẳng đã cho trên các trục tọa độ tương ứng. Giả sử rằng mặt phẳng tạo các giao của a, b và c trên ba trục tọa độ tương ứng. Như vậy, tọa độ giao điểm của mặt phẳng với các trục x, y và z lần lượt cho bởi (a, 0, 0), (0, b, 0) và (0, 0, c).


Thay các giá trị này vào phương trình tổng quát của một mặt phẳng, ta có
Aa + D = 0
Bb + D = 0
Cc + D = 0
Từ ba phương trình trên, ta có


Thay các giá trị này của A, B, c và D vào phương trình tổng quát của mặt phẳng, ta có


Điều này cho chúng ta phương trình cần thiết của một mặt phẳng ở dạng đánh chặn.
Xem thêm: