Phương trình của một mặt phẳng ở dạng chuẩn và Descartes

Vectơ của phương trình của một mặt phẳng ở dạng chuẩn bị cho bởi:

[latex] \ vec {r}. \ hat {n} = d [/ latex]

Trong đó [latex] \ vec {r} [/ latex] là vectơ vị trí của một điểm trong mặt phẳng, n là vectơ pháp tuyến đơn vị dọc theo pháp tuyến nối gốc với mặt phẳng và d là khoảng cách vuông góc của mặt phẳng từ gốc.

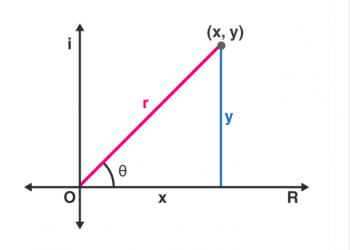
Gọi P (x, y, z) là một điểm bất kỳ trên mặt phẳng và O là gốc tọa độ. Sau đó chúng tôi có,

[latex] \ vec {OP} = \ vec {r} = x \ hat {i} + y \ hat {j} + z \ hat {k} [/ latex]

Bây giờ các cosin hướng của [latex] \ hat {n} [/ latex] là l , m và n được cho bởi:

[latex] \ hat {n} = l \ hat {i} + m \ hat {j} + n \ hat {k} [/ latex]

Từ phương trình [latex] \ vec {r}. \ Hat {n} [/ latex] = d, chúng ta nhận được

[latex] (x \ hat {i} + y \ hat {j} + z \ hat {k}). (l \ hat {i} + m \ hat {j} + n \ hat {k}) = d [/mủ cao su]

Do đó, dạng Descartes của phương trình mặt phẳng ở dạng chuẩn bị cho bởi:

lx + my + nz = d

Phương trình của mặt phẳng trong các ví dụ ở dạng chuẩn

Một ví dụ được đưa ra ở đây để hiểu phương trình của một mặt phẳng ở dạng chuẩn.

Ví dụ 1:

Một máy bay ở khoảng cách [latex] \ frac {9} {\ sqrt {38}} [/ latex] từ gốc tọa độ O. Từ điểm gốc, vectơ pháp tuyến của nó được cho bởi 5 [latex] \ hat {i} [/ latex] + 3 [latex] \ hat {j} [/ latex] – 2 [latex] \ hat {k} [/ latex] .

Phương trình vectơ đối với mặt phẳng là gì?

Giải pháp:

Gọi vectơ pháp tuyến là:

[latex] \ vec {n} = 5 \ hat {i} +3 \ hat {j} -2 \ hat {k} [/ latex]Bây giờ chúng ta tìm véc tơ đơn vị cho véc tơ pháp tuyến. Nó có thể được cung cấp bởi:

[latex] \ hat {n} = \ frac {\ vec {n}} {| \ vec {n} |} [/ latex]

[latex] \ hat {n} = \ frac {5 \ hat {i} +3 \ hat {j} -2 \ hat {k}} {\ sqrt {25 + 9 + 4}} [/ latex]

[latex] \ hat {n} = \ frac {5 \ hat {i} +3 \ hat {j} -2 \ hat {k}} {\ sqrt {38}} [/ latex]Vì vậy, phương trình yêu cầu của mặt phẳng có thể được đưa ra bằng cách thay nó vào phương trình vectơ là:

[latex] \ vec {r}. (\ frac {5} {\ sqrt {38}} \ hat {i} + \ frac {3} {\ sqrt {38}} \ hat {j} + \ frac {- 2} {\ sqrt {38}} \ hat {k}) = \ frac {9} {\ sqrt {38}} [/ latex]Ví dụ 2:

Tìm phương trình côsin của các mặt phẳng sau.

(a) [latex] \ vec {r}. (\ hat {i} + \ hat {j} – \ hat {k}) = 2 [/ latex]

(b) [latex] \ vec {r}. (2 \ hat {i} +3 \ hat {j} -4 \ hat {k}) = 1 [/ latex]

Giải pháp:

(a) [latex] \ vec {r}. (\ hat {i} + \ hat {j} – \ hat {k}) = 2 [/ latex] —- (1)

Chúng ta biết rằng với bất kỳ điểm bất kỳ, P (x, y, z) nào trên mặt phẳng, vectơ vị trí được cho là:

[latex] \ vec {r} = x \ hat {i} + y \ hat {j} + z \ hat {k} [/ latex]Bây giờ, thay giá trị của [latex] \ vec {r} [/ latex] vào phương trình (1), chúng ta nhận được

[latex] (x \ hat {i} + y \ hat {j} + z \ hat {k}). (\ hat {i} + \ hat {j} – \ hat {k}) = 2 [/ latex ]⇒ x + y – z = 2

Do đó, phương trình Descartes của mặt phẳng là x + y – z = 2.

(b) [latex] \ vec {r}. (2 \ hat {i} +3 \ hat {j} -4 \ hat {k}) = 1 [/ latex] —- (2)

Chúng ta biết rằng với bất kỳ điểm bất kỳ, P (x, y, z) nào trên mặt phẳng, vectơ vị trí được cho là:

[latex] \ vec {r} = x \ hat {i} + y \ hat {j} + z \ hat {k} [/ latex]Bây giờ, thay giá trị của [latex] \ vec {r} [/ latex] vào phương trình (2), chúng ta nhận được

[latex] (x \ hat {i} + y \ hat {j} + z \ hat {k}). (2 \ hat {i} +3 \ hat {j} – 4 \ hat {k}) = 1 [/mủ cao su]⇒ 2x + 3y – 4z = 1

Do đó, phương trình Descartes của mặt phẳng là 2x + 3y – 4z = 1.

Xem thêm: